§4 Нескінченно малі і нескінченно великі функції. Порівняння нескінченно малих

Функція називається нескінченно малою в точці , якщо . Функція називається нескінченно великою в точці , якщо 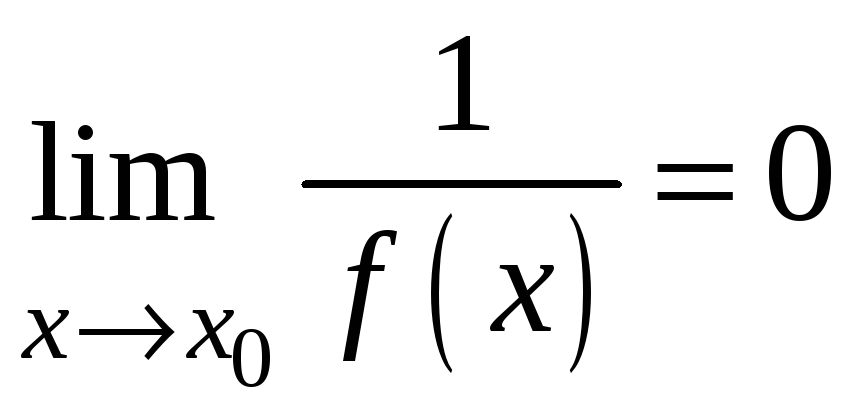. Пишуть . Наприклад, функція нескінченно велика в точці , оскільки функція нескінченно мала в цій точці.

Розглянемо дві нескінченно малі в точці функції і ( в , крім, можливо, самої точки ). Нехай .

Якщо , то будемо казати, що має більш високий порядок мализни, ніж . Пишуть в точці . Якщо , тобто , то, навпаки, . Якщо ж і , то кажуть, що і мають один і той же порядок мализни. У тому випадку, коли , нескінченно малі і називають еквівалентними. Пишуть , .

Теорема 4.3 ( принцип заміни нескінченно малих функцій на еквівалентні). Якщо при , то для будь-якої функції виконано рівності , , якщо границі в лівій і правій частинах існують.

§5 Деякі важливі границі

1.Справедлива рівність .

Наведемо у вигляді прикладів наслідки цієї важливої границі.

Приклад. Знайти .

Розв’язання. .

Приклад. Знайти .

Розв’язання. Виконаємо заміну змінної за формулою . Тоді у достатньо малому околі точки маємо . Отримаємо .

Приклад. Знайти .

Розв’язання. Аналогічно до попереднього прикладу можна отримати .

2. Справедлива рівність

, - ірраціональне число, . (4.1)

Приклад. Знайти .

Розв’язання. .

Приклад. Знайти .

Розв’язання. Виконаємо заміну змінної за формулою , тоді , . Отримаємо .

Враховуючи означення еквівалентних нескінченно малих, можна зробити висновок: , , , , , , коли.

§6 Розкриття деяких невизначеностей при обчисленні границь

1.Розкриття невизначеності виду при обчисленні границі частки двох многочленів при .

Приклад. Обчислити .

Розв’язання. Тут при і чисельник і знаменник дробу прямують до . В такому випадку кажуть, що має місце невизначеність виду . Розкрити невизначеність означає обчислити границю, або довести, що вона не існує. Розділимо чисельник і знаменник дробу на найстарший степінь . Отримаємо .

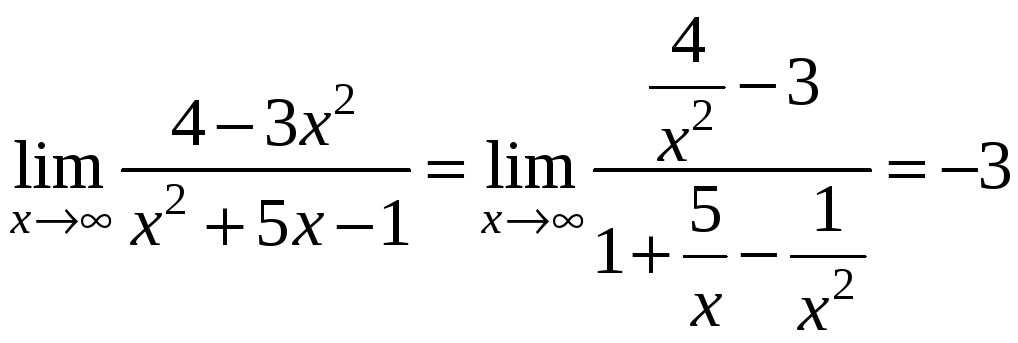Приклад. Обчислити .

Розв’язання. Розділивши чисельник і знаменник на , маємо .

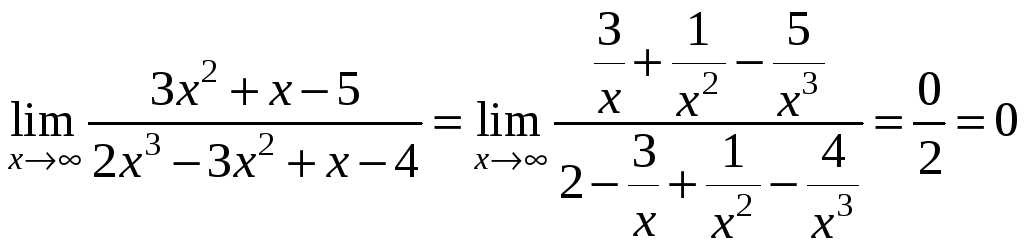Приклад. Обчислити .

Розв’язання. Аналогічно до двох попередніх прикладів маємо

.

Наведені приклади показують справедливість правила: границя частки двох многочленів при дорівнює

1. нулю, якщо степінь чисельника нижчий за степінь знаменника;

2. нескінченності, якщо степінь чисельника вищий за степінь знаменника;

3. відношенню старших коефіцієнтів чисельника і знаменника, якщо їх степені рівні.

Наприклад, , , .

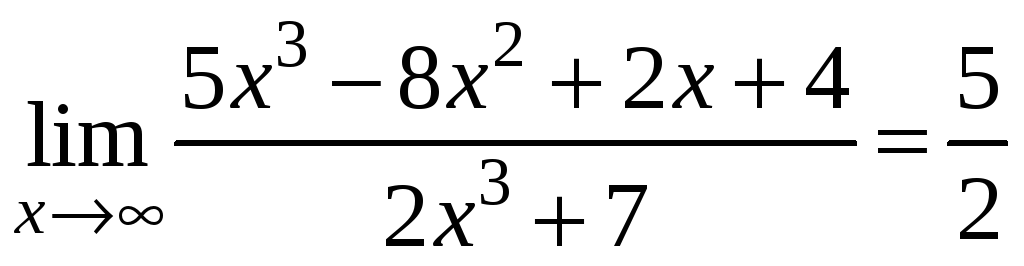2. Розкриття невизначеності виду при обчисленні границі частки двох многочленів.

Приклад. Знайти

Розв’язання. Тут при чисельник і знаменник прямують до нуля. Таку ситуацію називають невизначеністю виду . Розкладемо чисельник і знаменник на множники. 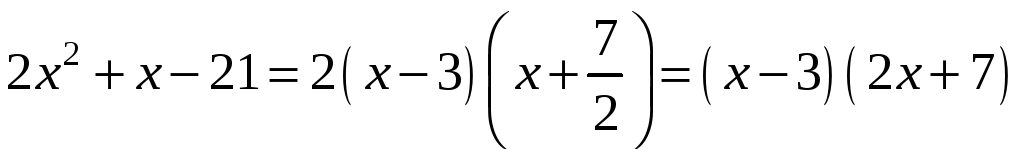за формулою , де - корені квадратного рівняння . В знаменнику за формулою скороченого множення маємо .

Тоді .

Таким чином, розкриття невизначеності при обчисленні границі частки двох многочленів при здійснюється шляхом скорочення дробу на двочлен .

3. Розкриття невизначеності виду при обчисленні границі деяких ірраціональних виразів.

Приклад. Знайти .

Розв’язання. Спочатку звільнимось від ірраціональності в знаменнику, а потім скоротимо дріб на .

.

4. Розкриття невизначеності виду при обчисленні границі деяких тригонометричних виразів.

Приклад. Знайти .

Розв’язання. .

Тут було використано теорему про заміну нескінченно малих функцій еквівалентними і той факт, що при .

Зауважимо, що аналогічний метод застосовується у прикладах, що містять множники або дільники виду та , де нескінченно мала функція.

5. Розкриття невизначеності виду .

У такому випадку користуються рівністю (4.1).

Приклад. Знайти .

Розв’язання.

.