2. Отношения и операции над нечеткими множествами

Определим следующие отношения нечетких множеств.

1. Включение (строгое и нестрогое). Пусть A и B – нечеткие множества на универсальном множестве E. Говорят, что A строго (нестрого) включено в B, если x E _A(x) > _B(x) (_A(x)  _B(x)). Обозначение: A  B (A  B).

2. Равенство. A и B равны, если xE _A(x) = _B(x).. Обозначение: A = B.

Операции над нечеткими множествами.

1. Дополнение. Пусть  = [0, 1], A и B – нечеткие множества, заданные на E. A и B дополняют друг друга, если xE _A(x) = 1 – _B(x). Обозначение: B = или A = . Очевидно, что . (Дополнение определено для M = [0,1], но очевидно, его можно определить для любого упорядоченного M).

2. Пересечение. A  B – наибольшее нечеткое подмножество, содержащееся одновременно в A и B;

_{A  B}(x) = min{_A(x), _B(x)}.

3. Объединение. А  В – наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности

_{A B}(x) = max {(_A(x), _B(x)}.

4. Разность. А \ B = А  с функцией принадлежности:

_A\B(x) = min { _A(x), 1 – _B(x)}.

Например, пусть: A = 0,4/ x₁  0,2/ x₂  0/ x₃  1/ x₄;

B = 0,7/ x₁  0,9/ x₂  0,1/ x₃ 1/ x₄; C = 0,1/ x₁  1/ x₂  0,2/ x₃  0,9/ x₄.

Здесь:

1. A  B, т.е. A содержится в B, С несравнимо ни с A, ни с B.

2. A  B  C.

3. = 0,6/ x₁  0,8/ x₂  1/ x₃  0/ x₄; = 0,3/ x₁  0,1/ x₂  0,9/ x₃  0/ x₄.

Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения _A(x), на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами.

Рис. 1. Рис. 2

 

  Рис. 3. Рис. 4.

На рис. 1 темная часть соответствует нечеткому множеству A и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в A. На Рис. 2 – 4 даны , A , A , соответственно.

Свойства операций  и .

Пусть А, В, С – нечеткие множества, тогда выполняются следующие соотношения:

а) – коммутативность;

б) – ассоциативность;

в) – идемпотентность;

г) – дистрибутивность;

д) A = A, где  – пустое множество, т.е. _(x)=0 xE;

A = ;

AE = A, где E – универсальное множество;

AE = E;

е) – теоремы де Моргана.

В отличие от четких множеств, для нечетких множеств в общем случае A , A  E, что, в частности, проиллюстрировано выше в примере наглядного представления нечетких множеств.

Алгебраические операции над нечеткими множествами

Алгебраическое произведение A и B обозначается AB и определяется так:

xE _AB (x) = _A(x)_B(x).

Алгебраическая сумма этих множеств обозначается А + В и определяется так:

xE _A+В(x) =  _A(x) + _B(x)_A(x)_B(x).

Для операций {, +} выполняются свойства:

• – коммутативность;

• – ассоциативность;

• A = , A+ = A, AE = A, A+E = E ;

• – законы де Моргана.

Не выполняются:

• – идемпотентность;

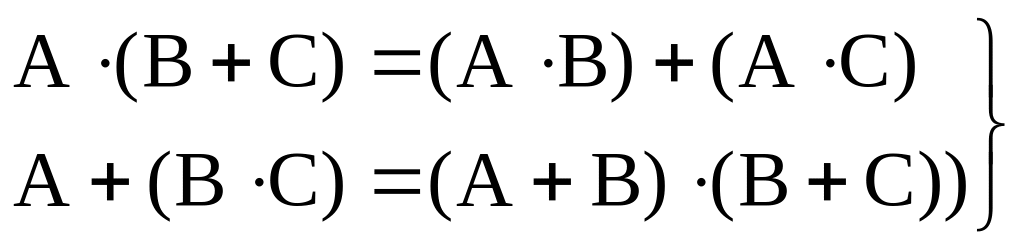• – дистрибутивность;

• а также A = , A+ = E.

Докажем первый закон де Моргана. Обозначим _A(x) через a, _B(x) через b. Тогда в левой части равенства для каждого элемента х имеем: 1– ab, а в правой, согласно формуле алгебраического сложения: (1– a) + (1– b) – (1 – a)(1 – b) = 1 – ab.

Докажем, что первое свойство дистрибутивности не выполня-ется, т.е. A(B + C)  (AB) + (AC). Для левой части имеем: a(b+c–bc) = ab + ac – abc; для правой: ab + ac – (ab)(ac) = ab + ac + a² bc. Это означает, что дистрибутивность не выполняется при aa².

Замечание. При совместном использовании операций {, ,,} выполняются свойства:

• А(B C) = (AB) (A  C);

• А (B C) = (AB) (AC);

• А+(B C) = (A+B) (A+C);

• А+ (B C) = (A+B) (A+C).