МАИ
А.А. Золотов
Методическое пособие к практическим занятиям
по курсу
Надежность и отработка ЛА(КА)
( специальность 1306, 1307 )
Утверждено на заседании каф.601
-------------------------------------------------------
2010
Занятие №1
Законы распределения случайных величин
Задание
1. Построить графики плотности распределения для различных законов распределения времени безотказной работы:
1.1. нормальный закон распределения;
1.2. закон распределения Релея;
1.3. закон распределения Вейбулла;
1.4. усеченного нормального закона распределения
1.5. логарифмически нормальный закон распределения.;
1.6. закона распределения Эрланга.
2. Подобрать законы распределения
для различных выборок представленных
в табл. 1.1 по критерию согласия Пирсона
--
.
Распределение числа попаданий
результатов измерений в интервалы
Таблица 1.1
N |
|
1 |
2 |
3 |
4 |
1 |
0—0.25 |
68 |
19 |
1 |
28 |
2 |
0.25—0.5 |
21 |
35 |
3 |
46 |
3 |
0.5—0.75 |
7.5 |
28 |
24 |
22 |
4 |
0.75--1 |
2.5 |
13 |
45 |
3 |
5 |
1—1.25 |
1 |
2 |
24 |
1 |
6 |
1.25—1.5 |
0 |
1 |
3 |
0 |
7 |
1.5—1.75 |
0 |
0 |
0 |
0 |
8 |
1.75--2 |
0 |
0 |
0 |
0 |
N |
|
5 |
6 |
1 |
0—1.5 |
5 |
24 |
2 |
1.5--3 |
47 |
31 |
3 |
3—4.5 |
27 |
21 |
4 |
4.5--6 |
12 |
12 |
5 |
6—7.5 |
6 |
6 |
6 |
7.5--9 |
2 |
3 |
7 |
9—10.5 |
1 |
2 |
8 |
10.5--12 |
0 |
1 |
Законы распределения :
1.
; Экспоненциальный
2.
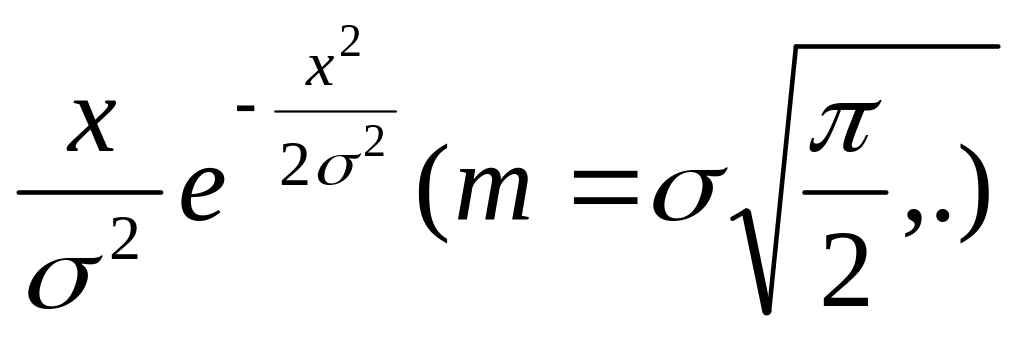; Релея
3.
;
Нормальный
4.
;
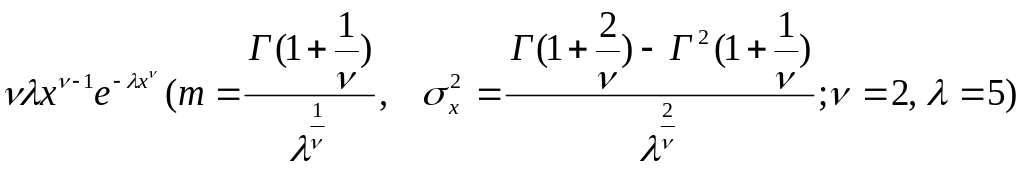Вейбулла
5.
;
Логарифмически-нормальный
6.
(
) ; Эрланга
Оценка математического ожидания и дисперсии:
Расчет выравнивающих частот
Вычисление
Квантили
распределения
Таблица 2.1
k |
|
||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,8 |
0,7 |
0,50 |
0,3 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
|
1 |
0 |
0,001 |
0,004 |
0,02 |
0,06 |
0,15 |
0,45 |
1,07 |
1,64 |
2,71 |
3,84 |
5,41 |
6,64 |
2 |
0,02 |
0,04 |
0,10 |
0,21 |
0,45 |
0,71 |
1,38 |
2,41 |
3,22 |
4,60 |
5,99 |
7,82 |
9,21 |
3 |
0,11 |
0,18 |
0,35 |
0,58 |
1,00 |
1,42 |
2,37 |
3,66 |
4,64 |
6,25 |
7,82 |
9,84 |
11,34 |
4 |
0,30 |
0,43 |
0,71 |
1,06 |
1,65 |
2,20 |
3,36 |
4,88 |
5,99 |
7,78 |
9,49 |
11,67 |
13,28 |
5 |
0,55 |
0,75 |
1,14 |
1,61 |
2,34 |
3,00 |
4,35 |
6,06 |
7,29 |
9,24 |
11,1 |
13,39 |
15,09 |
6 |
0,87 |
1,13 |
1,63 |
2,20 |
3,07 |
3,83 |
5,35 |
7,23 |
8,56 |
10,6 |
13,0 |
15,03 |
16,81 |
7 |
1,24 |
1,56 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,0 |
15,0 |
16,62 |
18,48 |
8 |
1,64 |
2,03 |
2,73 |
3,49 |
4,59 |
5,53 |
7,34 |
9,52 |
11,0 |
13,4 |
15,5 |
18,17 |
20,10 |
9 |
2,09 |
2,53 |
3,32 |
4,17 |
5,38 |
6,39 |
8,34 |
10,7 |
12,2 |
14,7 |
16,9 |
19,68 |
21,70 |
10 |
2,56 |
3,06 |
3,94 |
4,86 |
6,18 |
7,27 |
9,34 |
11,8 |
13,4 |
16,0 |
18,3 |
21,20 |
23,20 |
11 |
3,05 |
3,61 |
4,58 |
5,58 |
6,99 |
8,15 |
10,3 |
12,9 |
14,6 |
17,3 |
19,7 |
22,60 |
24,70 |
12 |
3,57 |
4,18 |
5,23 |
6,30 |
7,81 |
9,03 |
11,3 |
14,0 |
15,8 |
18,5 |
21,0 |
24,10 |
26,20 |
13 |
4,11 |
4,76 |
5,89 |
7,04 |
8,63 |
9,93 |
12,3 |
15,1 |
17,0 |
19,8 |
22,4 |
25,50 |
27,70 |
Задание №1
Рис. 1.1 Плотность нормального закона распределения.
Функция нормированного
нормального распределения
-
V
V
V
0,5
0
0,68
0,468
0,86
1,08
0,51
0,025
0,69
0,496
0,87
1,126
0,52
0,051
0,7
0,524
0,88
1,175
0,53
0,075
0,71
0,553
0,89
1,227
0,54
0,1
0,72
0,583
0,9
1,281
0,55
0,125
0,73
0,613
0,91
1,341
0,56
0,150
0,74
0,643
0,92
1,405
0,57
0,176
0,75
0,674
0,93
1,476
0,58
0,202
0,76
0,706
0,94
1,555
0,59
0,228
0,77
0,739
0,95
1,645
0,6
0,254
0,78
0,772
0,96
1,751
0,61
0,279
0,79
0,806
0,97
1,881
0,62
0,306
0,8
0,842
0,98
2,054
0,63
0,332
0,81
0,878
0,99
2,326
0,64
0,358
0,82
0,915
0,999
3,09
0,65
0,385
0,83
0,954
0,9999
3,72
0,66
0,412
0,84
0,995
0,99999
4,265
0,67
0,440
0,85
1,036
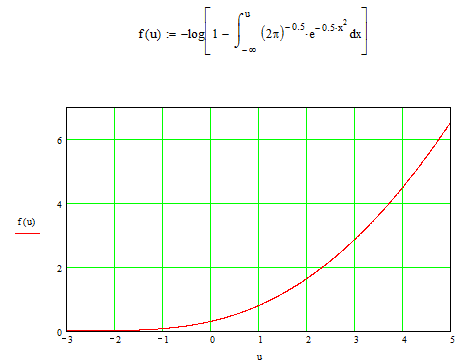
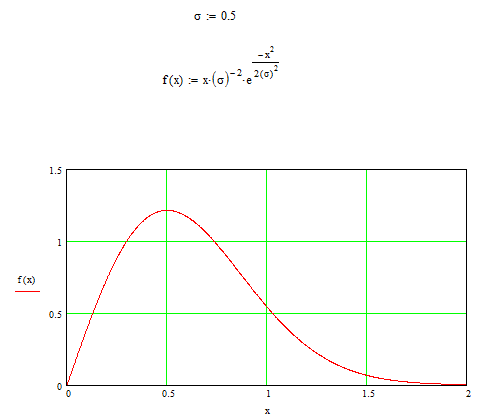
Рис. 1.2 Плотность закона распределения Релея.
Рис. 1.2 Плотность закона распределения Релея.
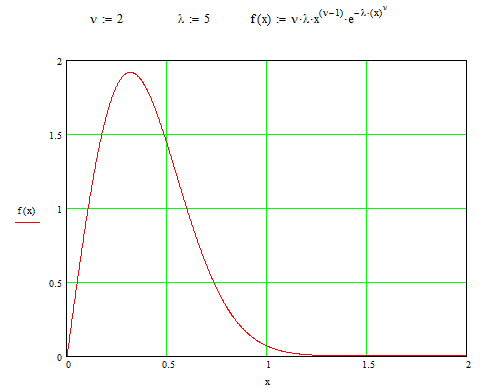
Рис. 1.3 Плотность распределения Вейбулла .
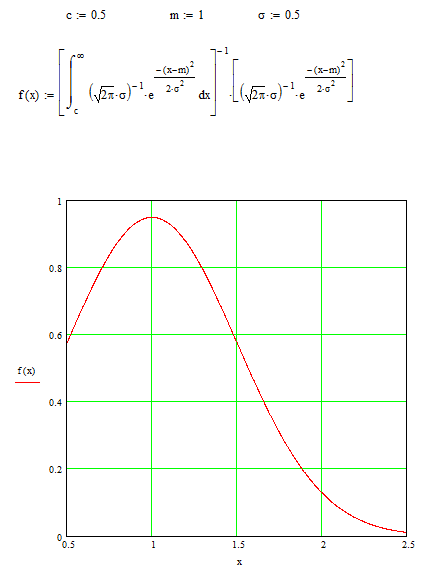
Рис. 1.4 Плотность усеченного нормального закона распределения.
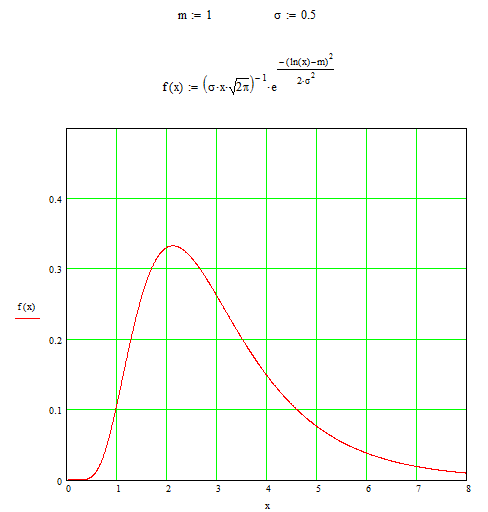
Рис.1.5 Плотность логарифмически нормального закона распределения.
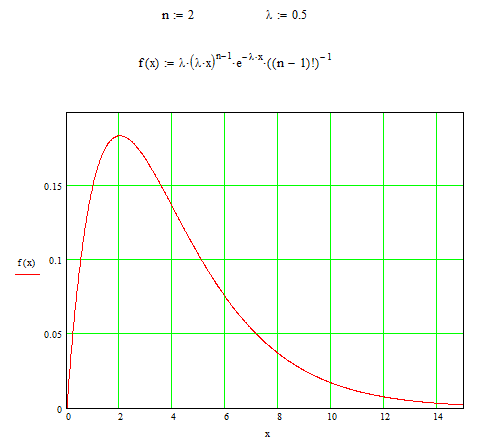
Рис.1.6 Плотность закона распределения Эрланга
Задание №2
2.1
2.2
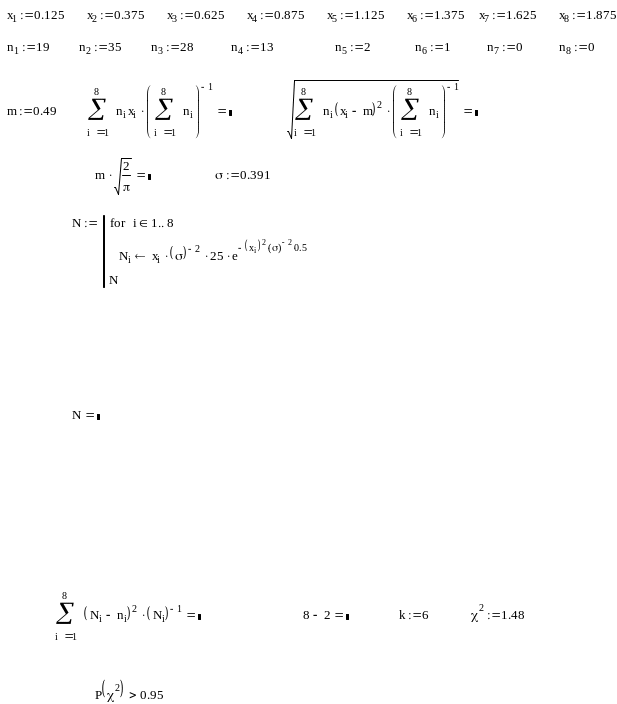
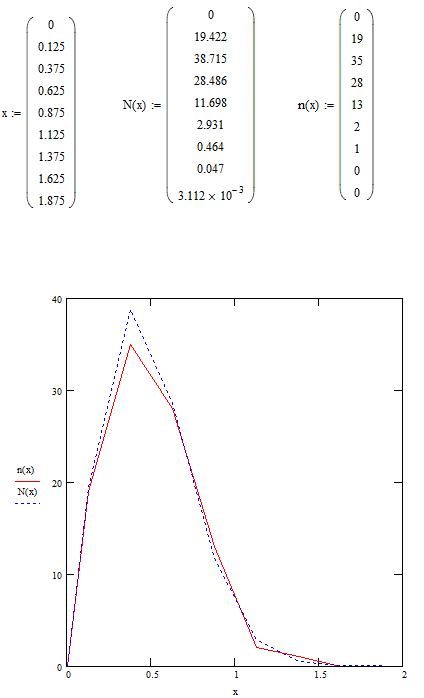
2.3
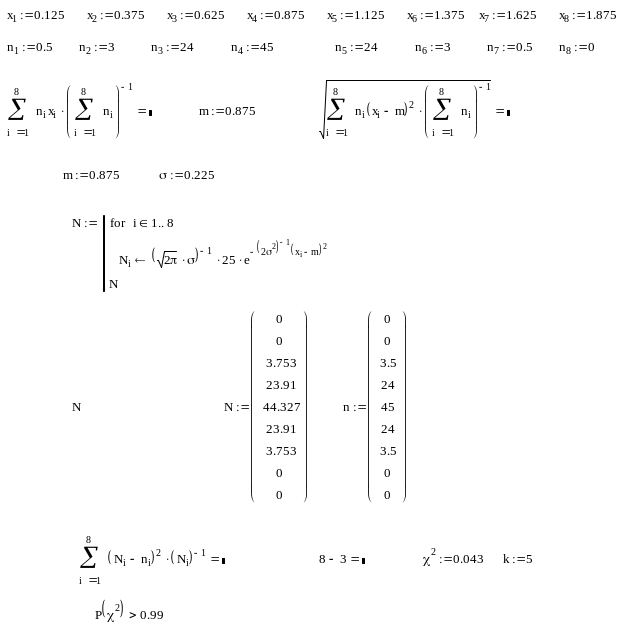
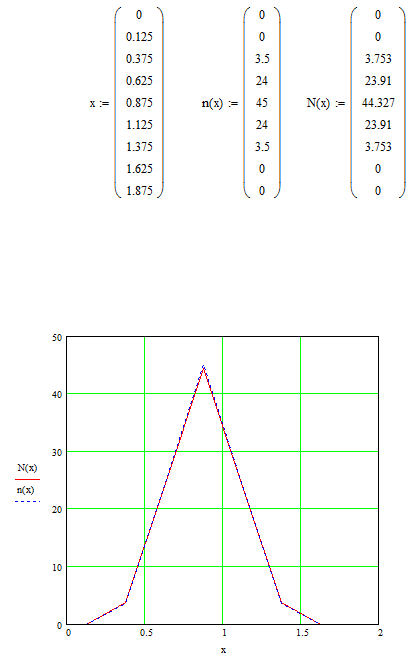
2.4
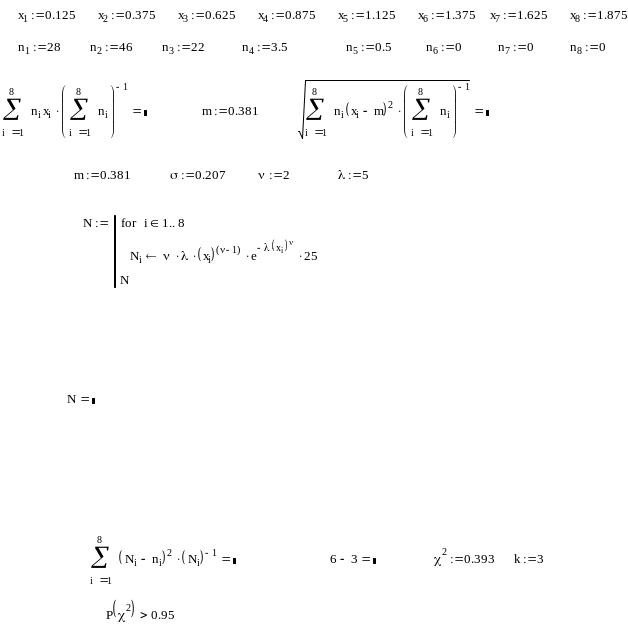
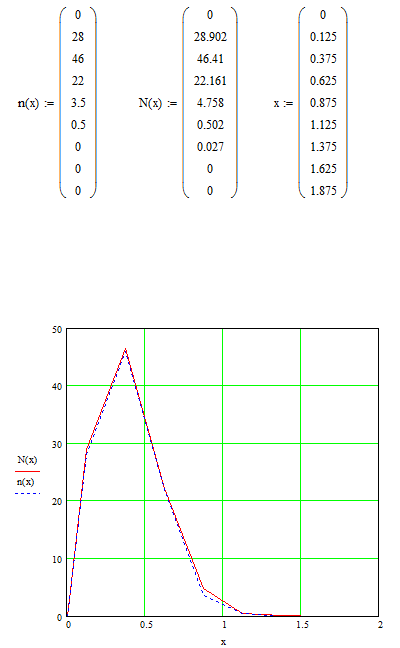
2.5
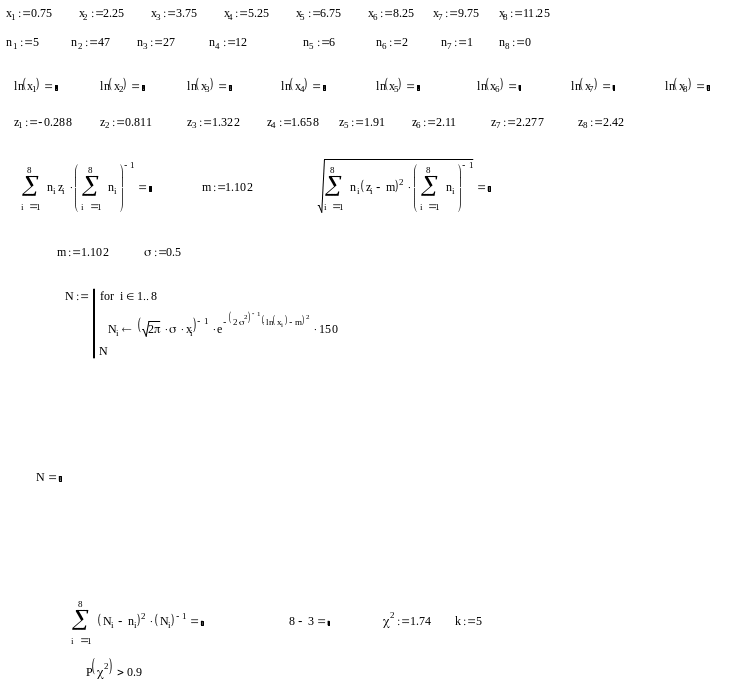
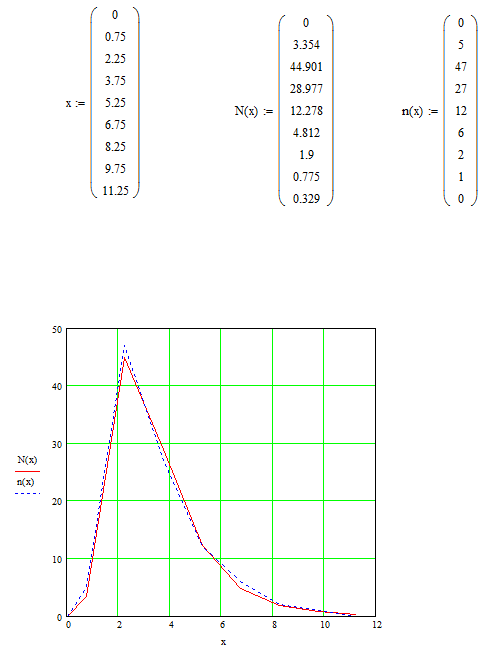
2.6
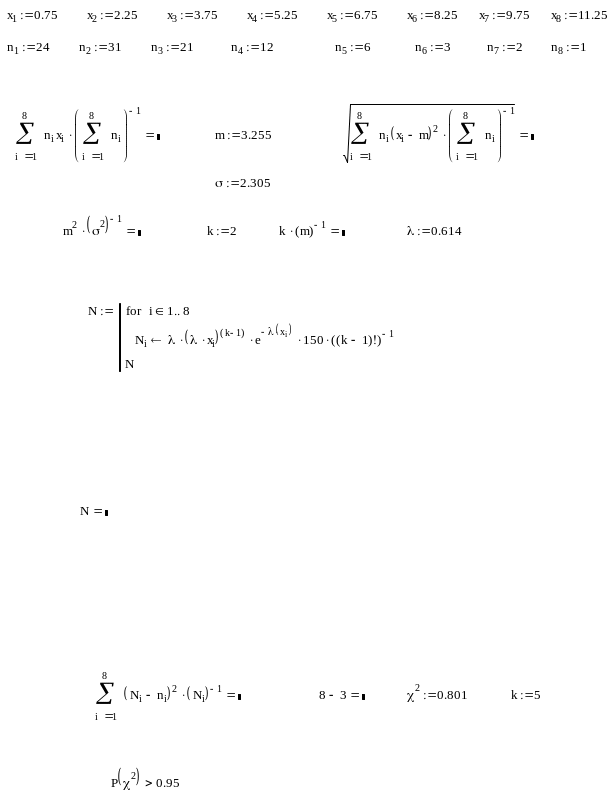
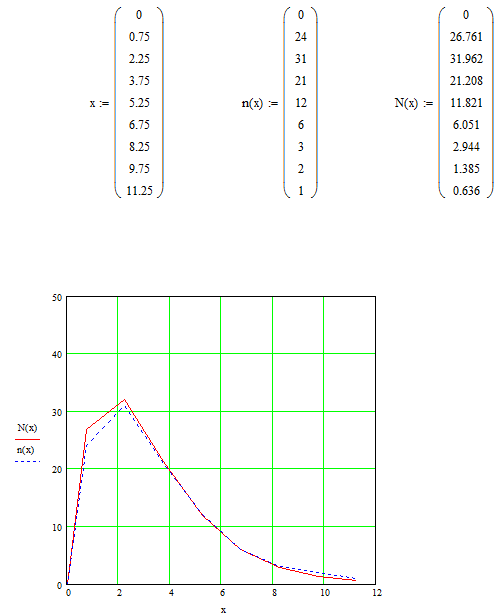
Занятие №2
Расчет надежности элемента.
Задание
1. Записать выражение для интенсивностей отказа различных законов распределения:
нормального, Релея, Вейбулла.
2.Рассчитать надежность раскрытия поворотной штанги антенны.
Исходные данные:
;
;
,
где N—работа движущих сил; R – работа сил сопротивления.
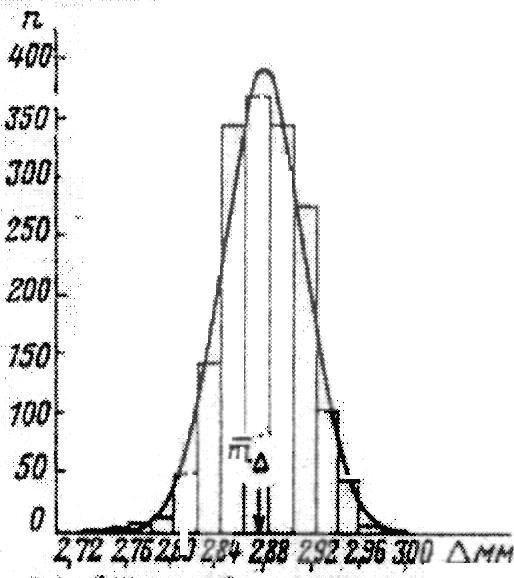
Рассчитать вероятность безударного разделения блоков.
Исходные данные:
мм
;
мм.
минимальное
расстояние между опасными точками
разделяемых блоков
4. Рассчитать надежность обечайки , нагруженной растягивающими усилиями при следующих исходных данных:
атм.;
1,5;
1,14
т/м; R=2 м; h=3м
;
320
МПа ;
3мм;
5%
;
5%
;
2%
;
3%.
5. Рассчитать надежность обечайки , нагруженной сжимающими усилиями при следующих исходных данных:
;
мм;
k=0,2, m==0,125;
n=0,25; N=200
Кн,
Кн,
Кн;
Законы распределения случайных параметров во всех заданиях считать нормальными.
Задание №1
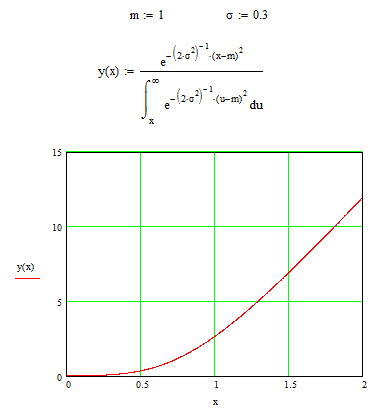
Рис. 1.1 Интенсивность отказа, соответствующая нормальному закону распределения.
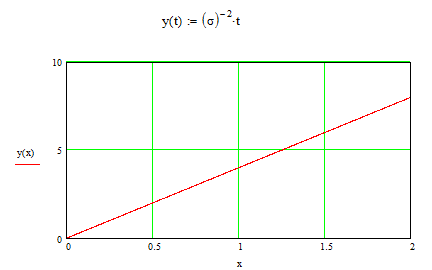
Рис..1.2 Интенсивность отказа, соответствующая закону распределения Релея.
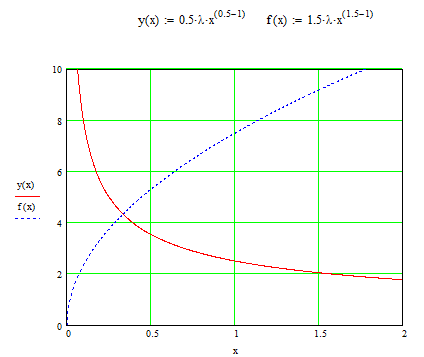
Рис.1..3. Интенсивность
отказа, соответствующая закону
распределения Вейбулла
.
Задание №2
;
;
.
Задание №3
Задание №4
При расчете гладких цилиндрических оболочек обычно рассматриваются следующие действующие напряжения:
1. Меридиональные
,
2. Кольцевые
,
где
внутреннее
избыточное давление; R—радиус
оболочки;
толщина
оболочки;
осевая
сжимающая сила и изгибающий момент;
осевая
перегрузка;
плотность компонента топлива;
высота
столба жидкости в баке.
В дальнейшем, для примера, рассмотрим
надежность конструкции оболочки бака,
работающего на внутреннее избыточное
давление. В этом случае коэффициент
запаса будет равен
, где
предел
прочности материала бака на растяжение;
Результаты расчета
представлены ниже:
;
;
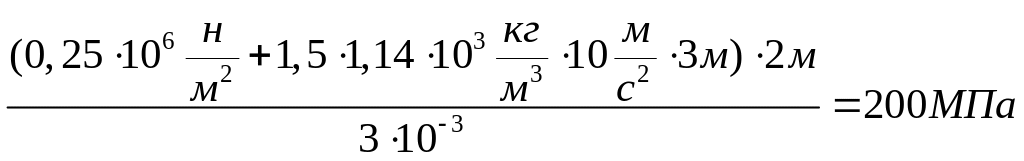Соответственно для коэффициентов вариации получим
;
;
.
Таким образом вероятность неразрушения оболочки будет равна
.
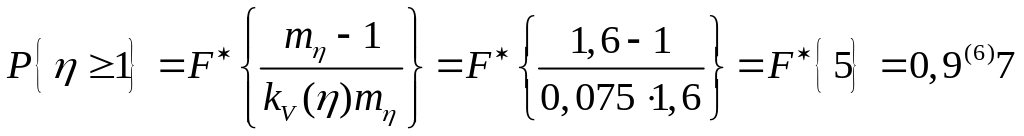Задание №5
При расчете на устойчивость критические нагрузки оцениваются по соотношению
.
Действующие усилия удобней представить в виде
.
Соответственно математическое ожидание
будет равно
,
где
.
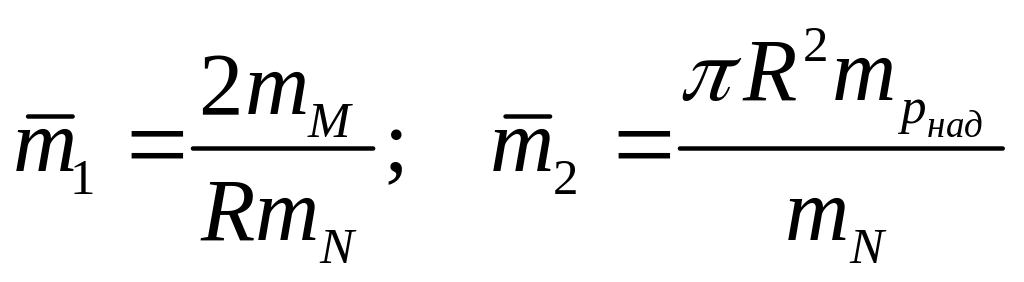Коэффициент вариации параметра
оценивается по соотношениям ( 1-- 3 ).
Результаты расчета
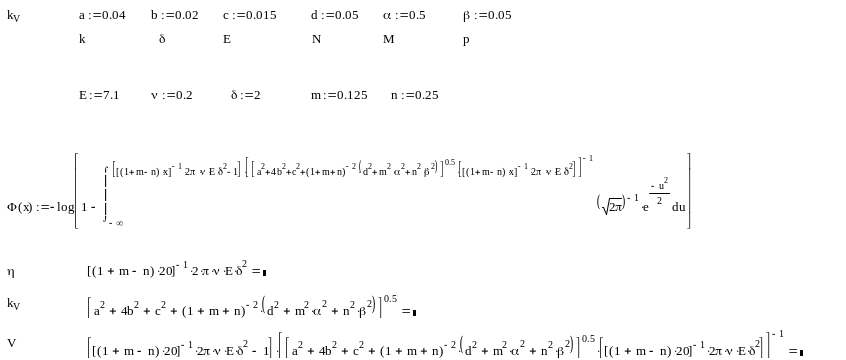
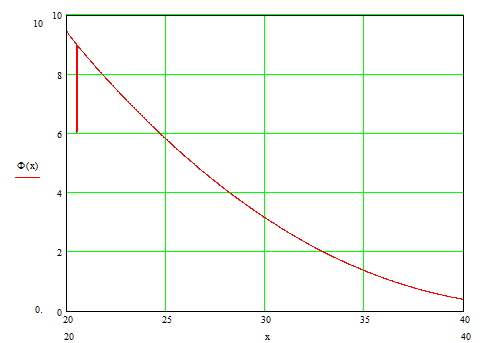
Рис. 1.1 Изменение уровня надежности, выраженной в белах, от уровня
нагружения отсека x=N.
Занятие №3
Расчет надежности систем.
Задание
1. Записать выражение для интенсивностей отказов различных систем:
1.1 системы с последовательным соединением элементов; 1.2. «горячего» резерва; 1.3. «холодного» резерва; 1.4 общего резерва.
2.Рассчитать надежность дублированной системы с «теплым» резервированием ( n=2)
3.Рассчитать надежность
системы с общим резервированием ( n=4;
).
4.Оценить среднее время работы системы с общим резервированием при исходных данных представленных в таблице 2
Таблица 2
Общее число элементов - n |
3 |
5 |
7 |
Число резервных элементов
-
|
1 |
2 |
3 |
При проведении расчетов
принять время работы системы t
=20 мес. , интенсивность отказа одного
элемента системы в рабочем режиме
.
При расчете «теплого»
резерва интенсивность отказа неработающего
элемента системы принять равной
.
5. Рассчитать надежность систем с последовательным и параллельным соединением зависимых элементов. Характер зависимости представлен на рис. 2.1,2.2.
Рис. 2.1 Зависимость
Рис. 2.2 Зависимость
( убывающая) ( возрастающая )
При проведении расчетов
для первого элемента принять:
. Для второго элемента принять
,
а значения
и
a
для каждой из кривых оценить по
графикам.
6 . Расчитать параметры систем с учетом требований по надежности:
6.1.Рассчитать потребную кратность резерва: «горячий» резерв; «холодный» резерв. Исходные данные: H=0.999; h=0.9 , где h—надежность нерезервированного элемента.
6.2.Восстановить структурную схему надежности по соотношениям, используемым для расчета надежности:
1 )
2 )
6.3 Оценить допустимое количество разрывных болтов в разъемном стыке.
Исходные данные:
;
.
7. Рассчитать надежность раскрытия пирозамков крепления лобового экрана СА, используя модель цепи. Исходные данные: работа движущих сил N=50;
работа сил сопротивления R=30; число пирозамков n=8.
Задание №1
1.1. Последовательная схема
,
.
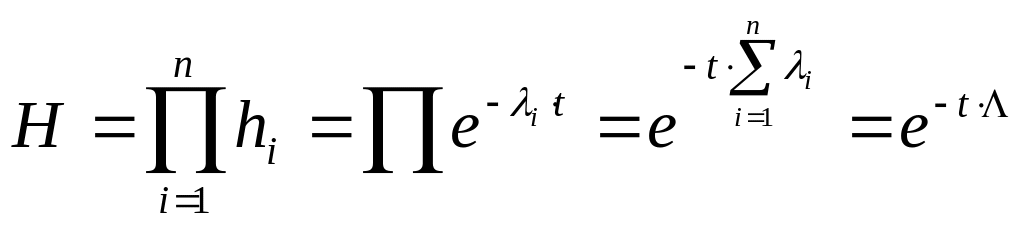1.2. «Горячий» резерв
lim
Рис. 1.2 Зависимость интенсивности отказа f(x) от времени работы x.
1. 3. «Холодный» резерв
lim
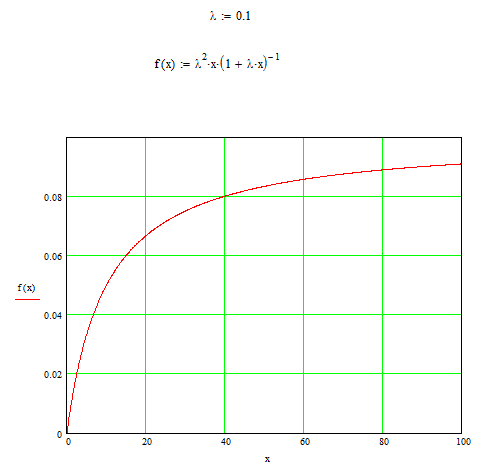
Рис. 1.3. Зависимость интенсивности отказа f(x) от времени работы x.
1. 4. Общий резерв
;
; lim
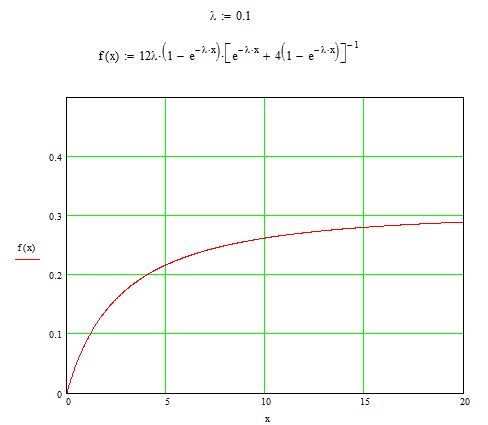
Рис. 1.4. Зависимость интенсивности отказа f(x) от времени работы x.
Задание №2
Граф переходов:
переход
происходит с интенсивностью
переход
происходит с интенсивностью
Составляем уравнения Колмогорова:
;
;
;
;
;
;
Рис. 2. 1 Зависимость надежности, выраженной в белах, от уровня интенсивности отказа x=
Задание №3
Граф переходов
переход
происходит с интенсивностью
переход
происходит с интенсивностью 3
Уравнения Колмогорова
;
;
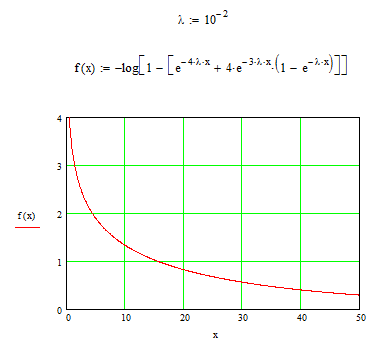
Рис. 3. 1 Зависимость надежности, выраженной в белах, от времени работы системы.
Задание №4
(первый вариант)
Граф переходов
переход
происходит с интенсивностью
переход
происходит с интенсивностью
Задание №5.
Последовательная схема
( рис. 2.1 ,кривая 1 )
=
=
=
=
.
( рис.2.1,кривая 2 )
( рис. 2.2, кривая 1 )
( рис.2.2,кривая 2 )
Параллельная схема
( рис. 2.1 ,кривая 1 )
( рис.2.1,кривая 2 )
=
=
=
( рис. 2.2 ,кривая 1 )
( рис.2.2,кривая 2 )
=
Задание №6
6.1)
«Горячий резерв»
«Холодный» резерв
.
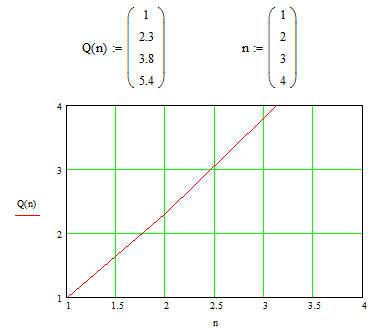
Рис. 6.1 Характер изменения надежности системы, выраженной в белах от кратности резерва
6.3)
;
Задание №7.
Оценка надежности по модели цепи
,
где
;
.
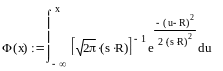2. Сравнительная оценка
логарифмов значений интеграла
(x)
и аппроксимирующей зависимости для
этого интеграла y(x)
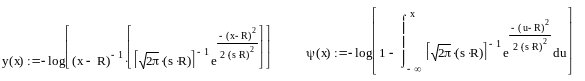
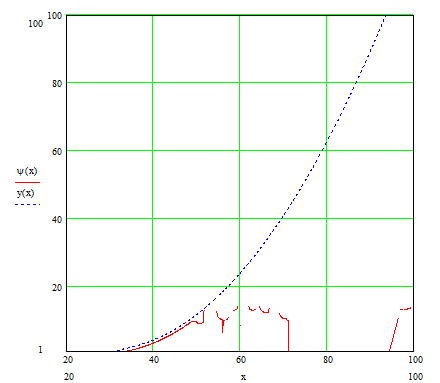
Рис. 7.1 Сравнительная оценка логарифмов значений интеграла (x) и аппроксимирующей зависимости для этого интеграла y(x) .
Результаты проведения расчетов надежности раскрытия, выраженной в белах
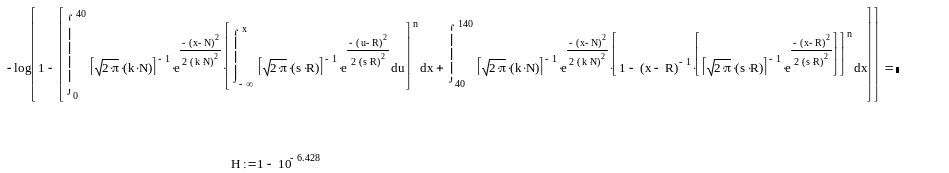
Оценка надежности по приближенной модели модели
;
;
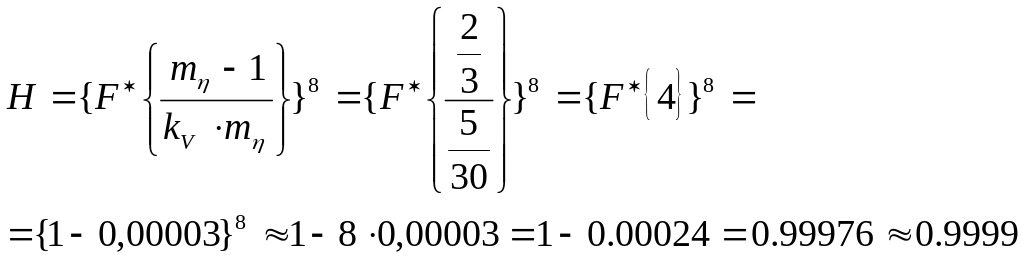
Занятие №4
Нормирование надежности.
Расчет характеристик восстанавливаемых систем.
Задание
1. Провести нормирование элементов системы с «холодным» или «горячим» резервом. Закон распределения наработки на отказ отдельных элементов принять экспоненциальным.
Исходные данные:
1.1 Система с «горячим» резервом (два элемента)
1.2 Две системы H=0.98. Исходные данные по стоимости нерезервированных систем с и вероятности отказа этих систем q представлены на рис. 1.1
. Первая система имеет «горячий» резерв(
,
вторая система имеет «холодный» резерв
.
Параметр
характеризует кратность резерва, которая
итерационно уточняется.
1.3 Пронормировать систему из двух элементов, вероятность отказа которых подчиняется соотношению:
, где
коэффициенты
аппроксимации;
--
масса i-ой
системы.
2.Рассчитать коэффициент
готовности для резервированной системы
с восстановлением отказавших элементов
в случае «горячего» резерва. При решении
задачи принять :
.
.
Общее число элементов n
= 2.
3.Рассчитать коэффициент готовности для резервированной системы с восстановлением отказавших элементов в случае «холодного» резерва. При решении задачи принять : . Общее число элементов n = 2.
4.Рассчитать коэффициент готовности для резервированной системы с восстановлением отказавших элементов в случае общего резерва. При решении задачи принять : ,
Общее число элементов n
= 3 ; число резервных элементов
;
5.
Рассчитать значения коэффициента
готовности
для резервированной системы с
восстановлением отказавших элементов.
При проведении расчетов принять
1/мес.;
1/мес. Количество элементов представлено
в таблице.
Общее число элеиентов N |
Число рабочих элементов n |
Число ремонтных устройств r |
3 |
1 |
3 |
4 |
2 |
2 |
5 |
2 |
4 |
6. Рассчитать показатели функционирования технической системы со следующими характеристиками
Задание №1
При использовании уже существующих элементов, задача обеспечения заданных уровней надежности системы может быть решена использованием структурного резервирования.
При решении
поставленной задачи примем, что
вероятность безотказной работы
нерезервированного i-ого
элемента
за период Tr
оценивается по произвольному закону
распределения F(x)
h0i = 1 – F(Tr)
Соответственно вероятность отказа i-ого нерезервированного элемента будет равна
q0i = 1 – h0i.
При структурном резервировании
вероятность отказа i-го
элемента
,
может быть оценена по приблизительному
соотношению, соответствующего
резервированию с замещением отказавшего
элемента («холодный» резерв) [18]
, где
общее
число элементов в резервной группе (
кратность резерва ).
Производя логарифмирование, получим
.
В
дальнейшем соотношение представим в
виде
Затраты на производство и эксплуатацию i-ого элемента системы будут равны
СЭi = C0imi , где СЭi – стоимость i-ой системы.
Полученные
результаты позволяют перейти к решению
задачи нормирования надежности элементов,
то-есть оптимального распределения
уровней надежности между отдельными
элементами системы, обеспечивающих
удовлетворение заданных требований к
надежности системы в целом при минимальном
расходе средств на реализацию целевой
программы. Очевидно, затраты на
производство и эксплуатацию системы,
состоящей из n элементов,
будут равны
.
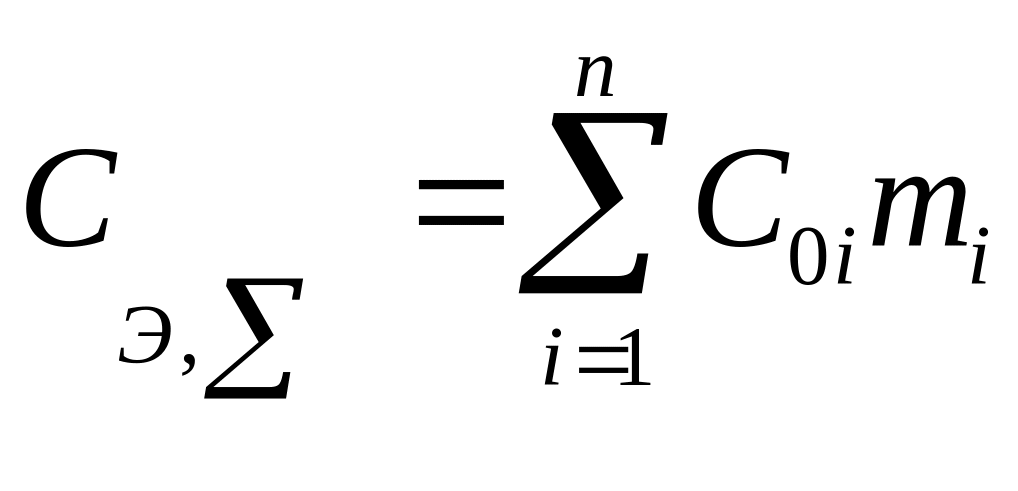Соответственно надежность системы,
состоящей из n последовательно
соединенных элементов, будет равна
.
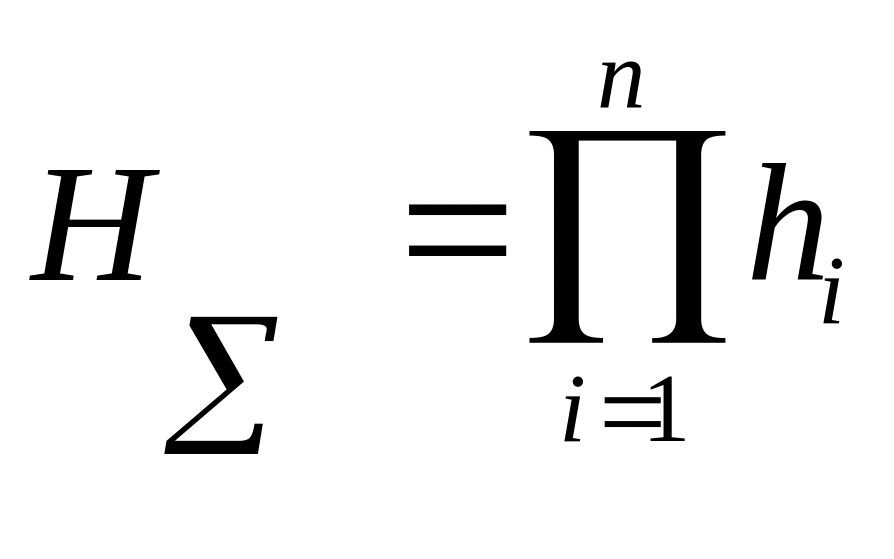Для высоконадежных систем вероятность отказа можно оценить по приближенному соотношению
,
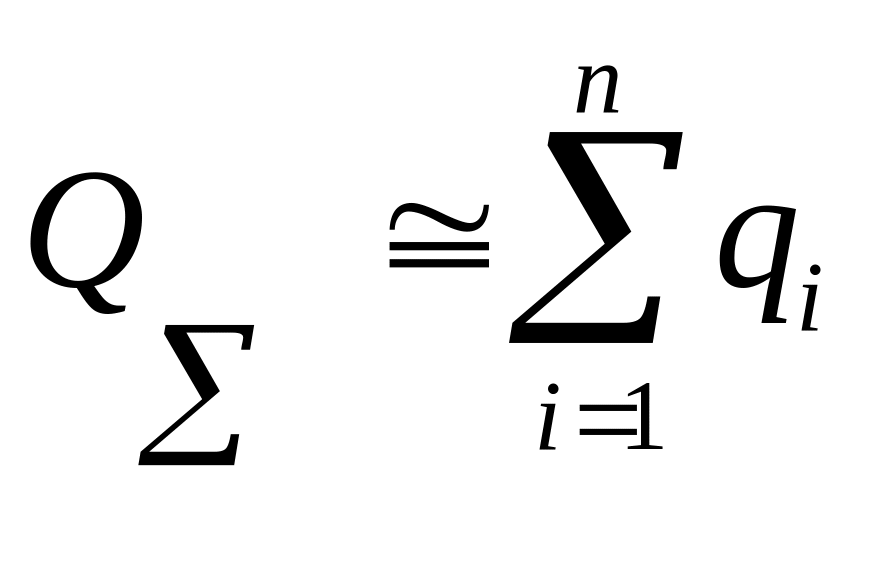где qi
= 1 – hi.
Очевидно заданные требования к надежности системы могут быть обеспечены при различных комбинациях значений слагаемых qi. Среди множества значений qi целесообразно выбрать такие, которые обеспечивают минимум затрат на реализацию целевой программы. Поставленную задачу будем решать методом Лагранжа.
В рассматриваемом случае функция Лагранжа примет вид
,
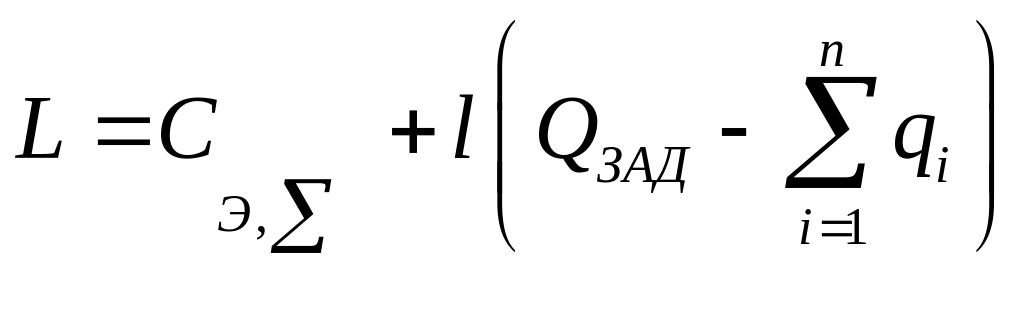где l – множитель Лагранжа.
При этом оптимальные уровни qi,
должны удовлетворять условию
.
Раскрывая выражение производной, получим
,
Производная от затрат по qi оценивается по соотношению
,
где
.
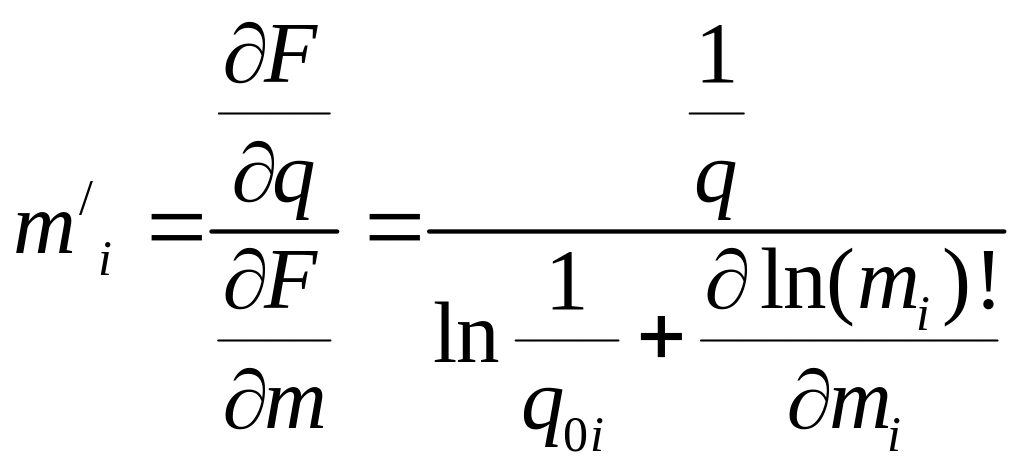Для нахождения производной воспользуемся приближенной оценкой функционала m!.
Предполагая,
что дискретная функция
может быть аппроксимирована непрерывной
зависимостью, проведем формальное
дифференцирование
.
Таким образом, окончательно получим
,
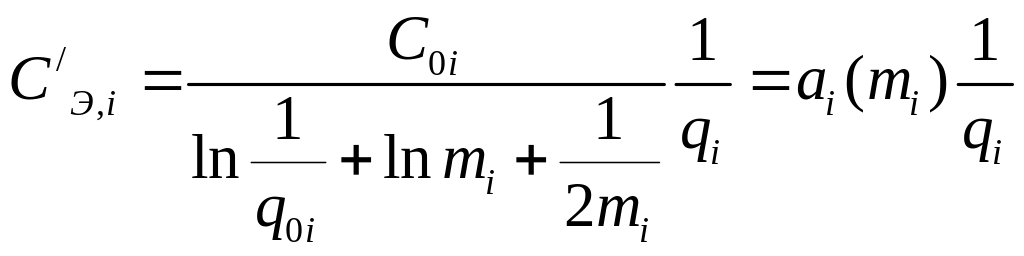где
.
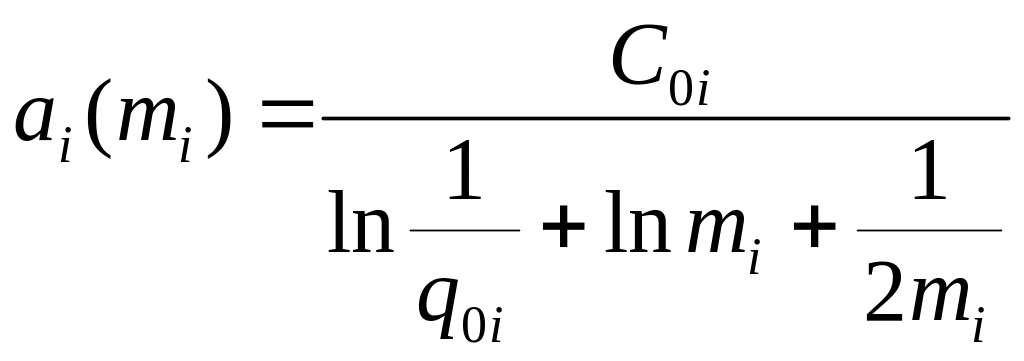После подстановки
в
условие оптимальности найдем
.
С учетом выражения для дисциплинирующее условие примет вид
.
.
Разрешая это соотношение относительно неопределенного множителя Лагранжа , найдем
.
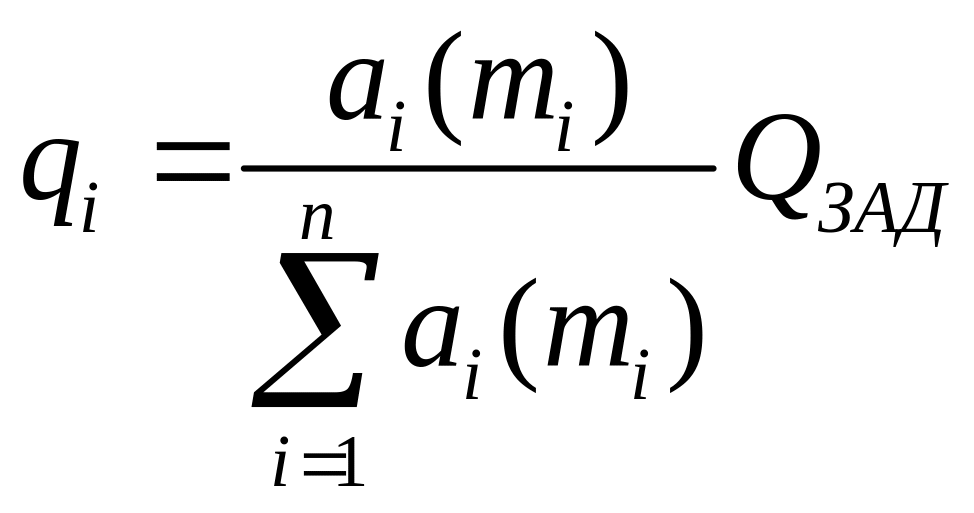Окончательный результат можно получить методом последовательных приближений. В качестве нулевого приближения можно принять равномерное распределение надежности
.
Знание
позволяет найти оценку
из соотношения
.
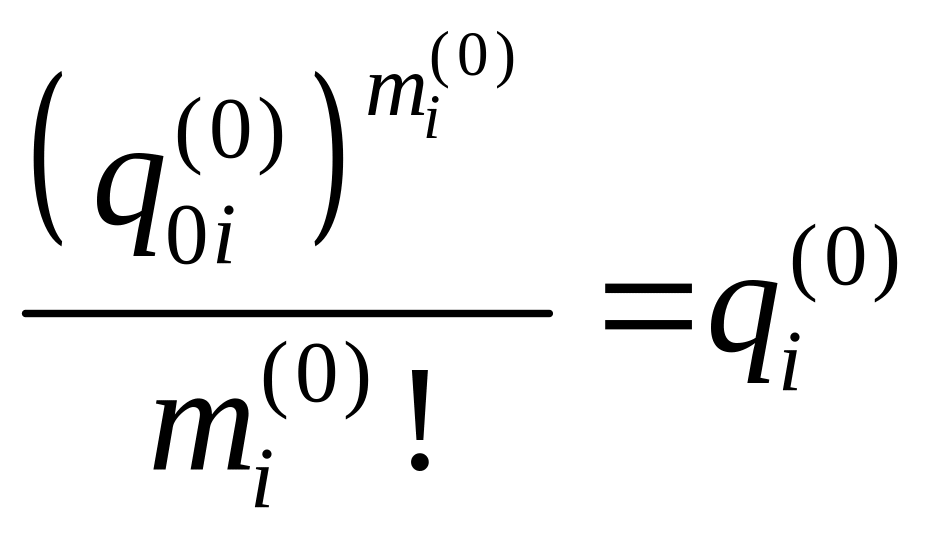Итерационный процесс заканчивается по достижении требуемой точности вычислений.
В случае «горячего» резерва, при
проведении расчетов, следует принять
.
Отсюда
.
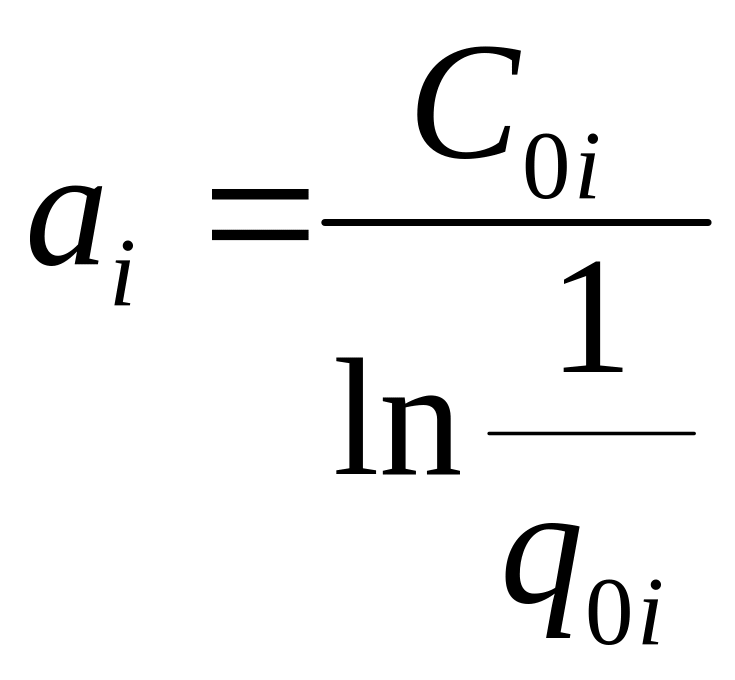При этом кратность резерва рассчитывается по соотношению
,
где
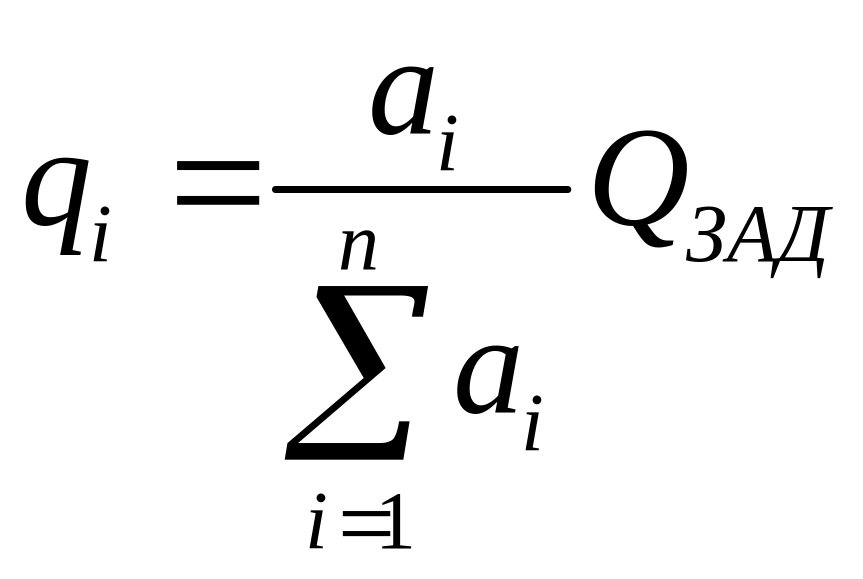
Задание 1.1 .
Расчет проводился по соотношениям:
при «горячем» резервировании кратность резерва оценивается по соотношению
,
где
,.
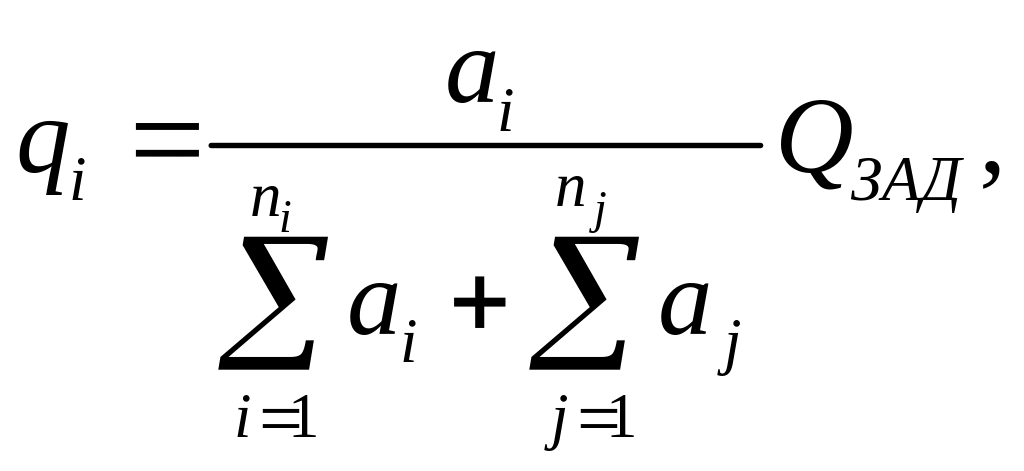Результаты расчета представлены на рис. 1.1
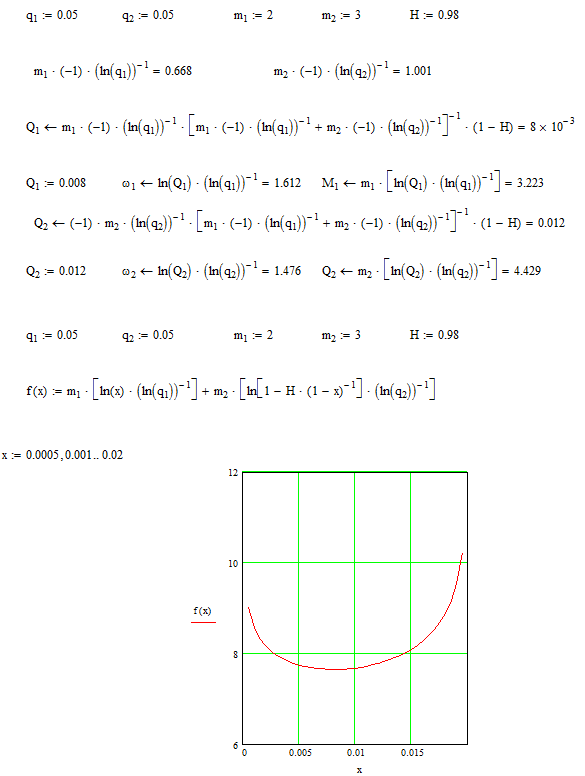
Рис. 1.1 Зависимость
суммарных затрат от
.
Задание 1.2.
Исходные
данные по стоимости нерезервированных
систем
и вероятности отказа этих систем
представлены ниже:
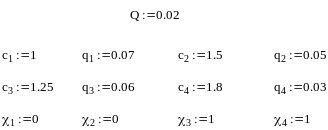
Первые две системы имеют «горячий» резерв( , две последние системы имеют
«холодный» резерв .
Для удобства проведения расчетов по программе Mathcad при формировании, представленных выше, исходных данных были приняты следующие обозначения:
,
.
Программа и результаты расчета представлены ниже.. Параметр , используемый в программе, характеризует кратность резерва, которая итерационно уточняется.
Окончательно кратности резерва записываются в виде матрицы-столбца R .
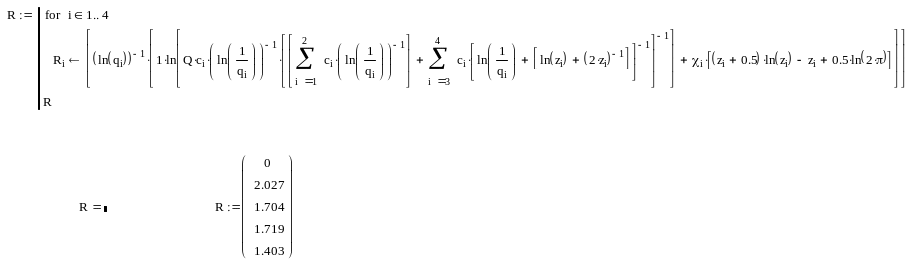
Расчет проводился по соотношениям:
при «горячем» резервировании кратность резерва оценивается по соотношению
,
где ,.
при «холодном» резервировании кратность резерва находится из соотношения
,
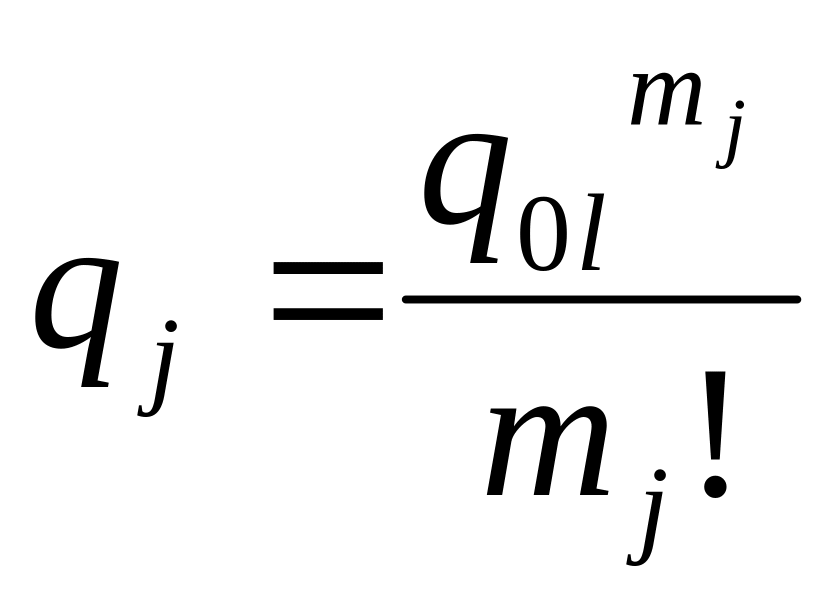где
,
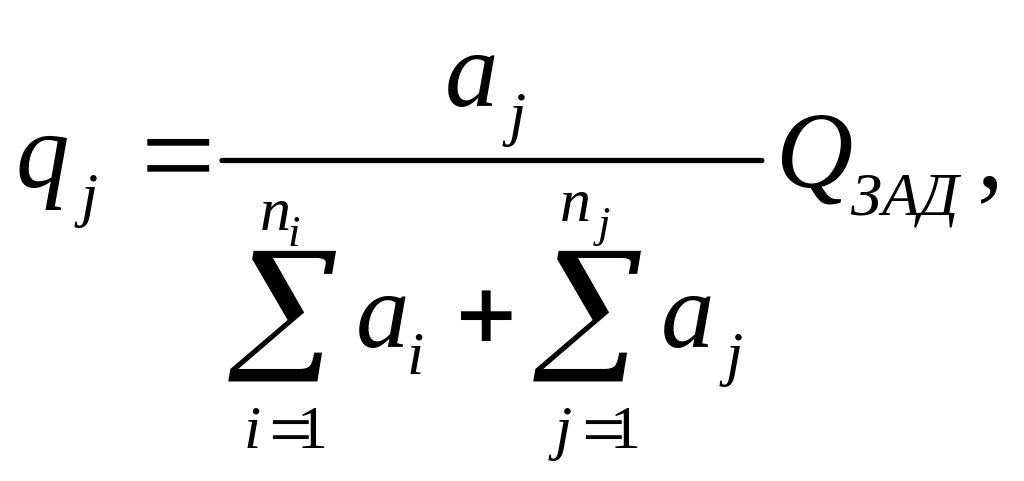
Задание № 1.3
Дисциплинирующее условие:
Целевая функция:
Функция Лагранжа:
Условие оптимальности:
Расчет соотношений для оптимальных уровней вероятности отказа:
;
;
;
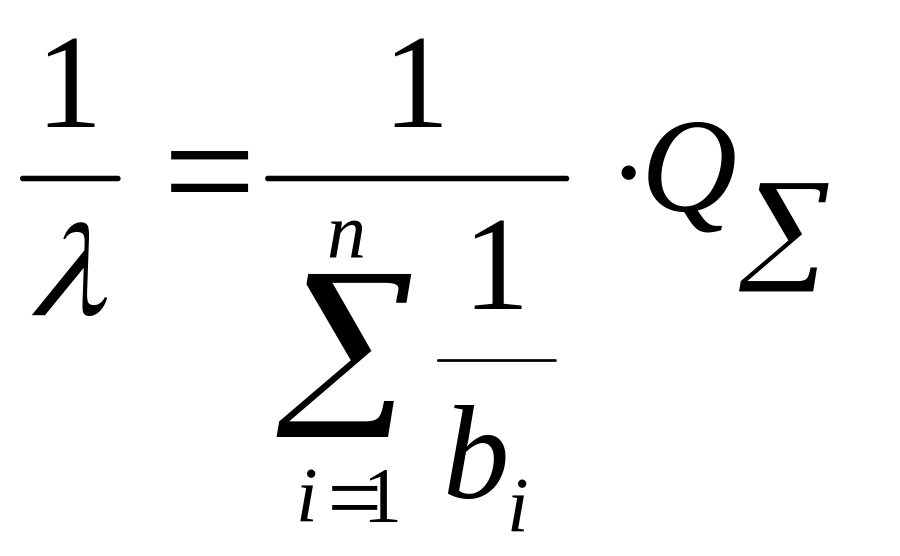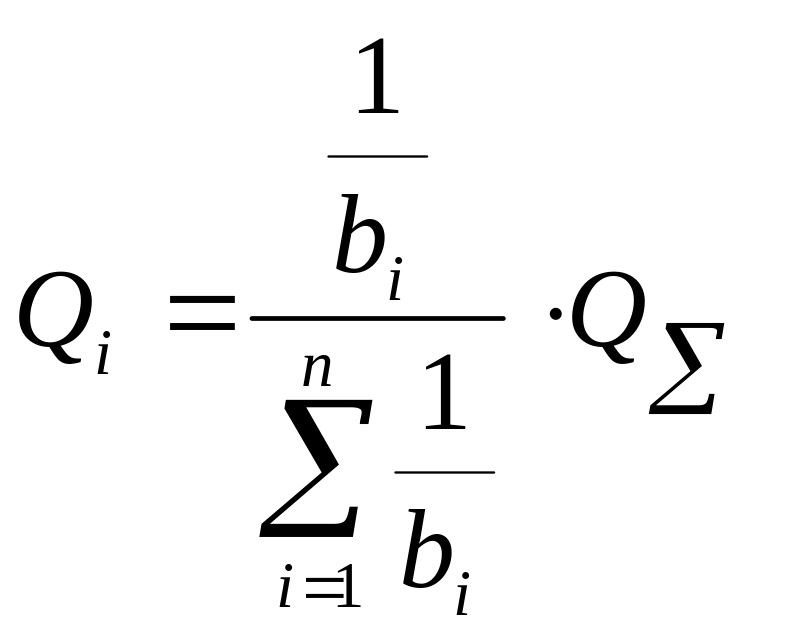
Расчет оптимального распределения масс:
;
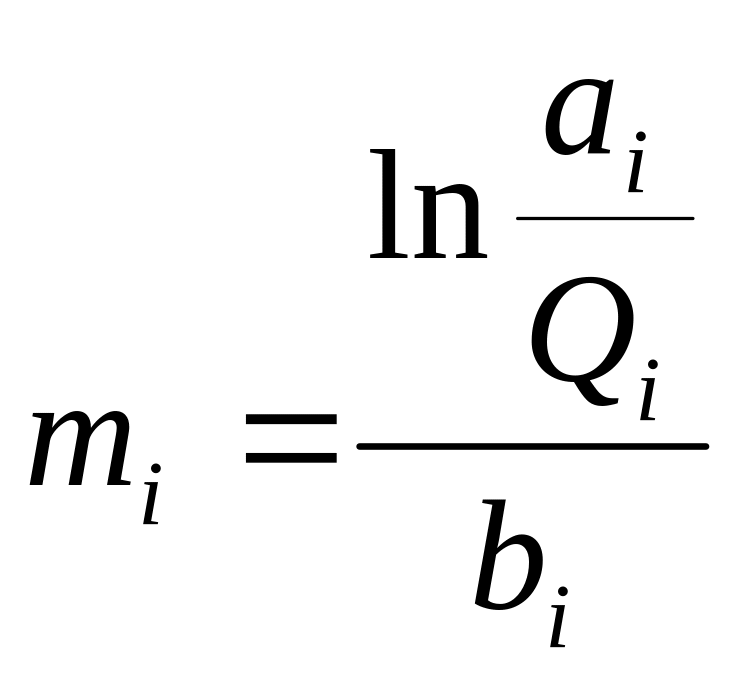
Результаты расчета по оптимальным соотношениям и результаты численной оптимизации методом перебора представлены ниже.
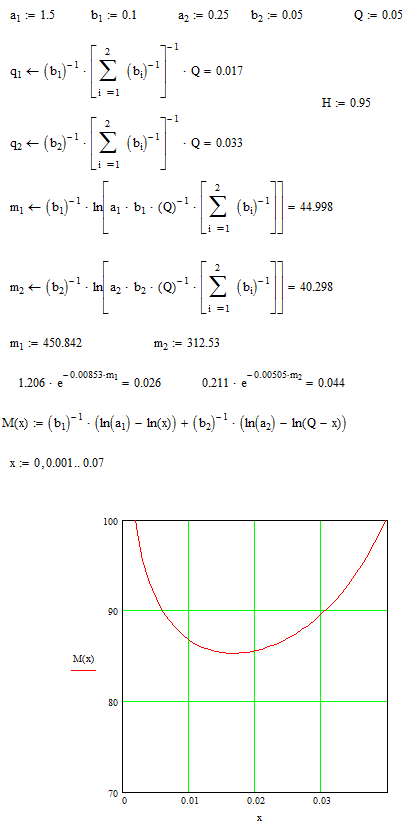
Задание №2
Граф состояний
Переходу
соответствует интенсивность
,
а
интенсивность
Переходу
соответствует интенсивность
,
а
интенсивность
;
.
;
;
=
=
Задание №3
Граф состояний
Переходу соответствует интенсивность , а интенсивность
Переходу соответствует интенсивность , а интенсивность
;
.
;
;
=
=
Задание №4
Граф состояний
Переходу соответствует интенсивность 3 , а интенсивность
Переходу соответствует интенсивность 2 , а интенсивность
Переходу
соответствует интенсивность
,
а
интенсивность
;
;
;
;
;
;
.
Задание №5
Рассмотрим решение задачи для исходных данных, соответствующих первой строчке таблицы. Граф состояний такой системы примет вид, представленный на рис. 1.
Рис.5. 1. Граф состояний системы.
Для представленного графа получим
.
Вероятность
оценивается из условия нормировки
.
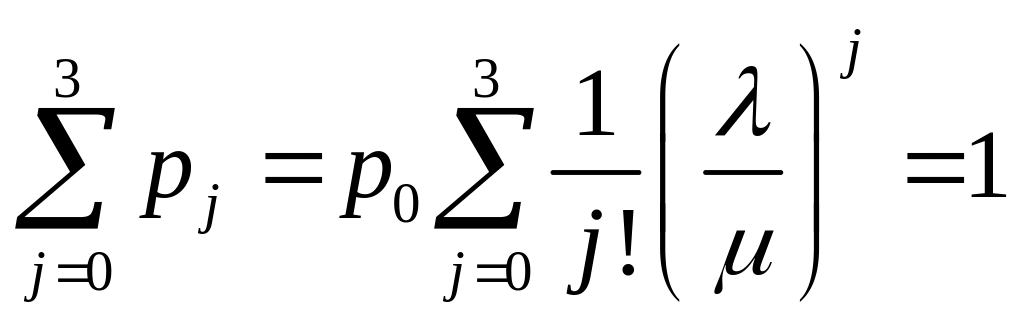Таким образом окончательно найдем
.
При
этом коэффициент готовности оценивается
по соотношению
.
Результаты расчета представлены на рис. 4.2
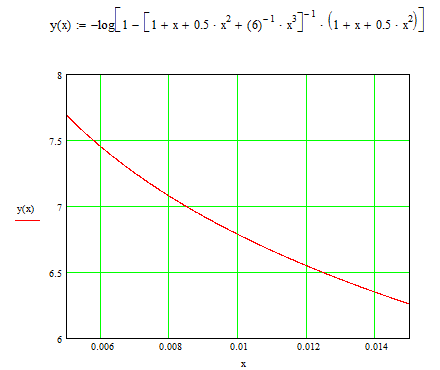
Рис.
5.2 Изменение коэффициента готовности,
выраженного в белах, в зависимости от
параметра
.
Задание №6
Рассмотрим систему в составе которой находится N элементов, из которых n -- рабочих .
При анализе ремонтопригодности системы будем считать, что каждый отказавший элемент идет в ремонтное устройство, состоящее из r единиц. Если все ремонтные единицы заняты восстановлением, то элемент становится в очередь Таким образом каждый элемент в процессе работы системы многократно проходит цикл:
работа---ожидание ремонта---ремонт---резерв.
Пусть
среднее
время пребывания элемента в рабочем
состоянии,
среднее
время ожидания ремонта,
среднее
время ремонта,
среднее
время пребывания в резерве.
Обозначим
.
Тогда отношения
будут определять среднюю долю времени, которое элемент пребывает в том или ином состоянии. Очевидно, введенные коэффициенты ,будут так же характеризовать относительное среднее число элементов, находящихся в том или ином состояниях
,
где
число
элементов, находящихся в момент t
в i – том состоянии;
среднее число элементов, находящихся
в рабочем состоянии;
среднее число элементов, находящихся
в ожидании ремонта;
среднее
число элементов, находящихся в ремонте;
среднее число элементов, находящихся
в резерве.
Очевидно, значения
удовлетворяют соотношениям
{
{
{
{
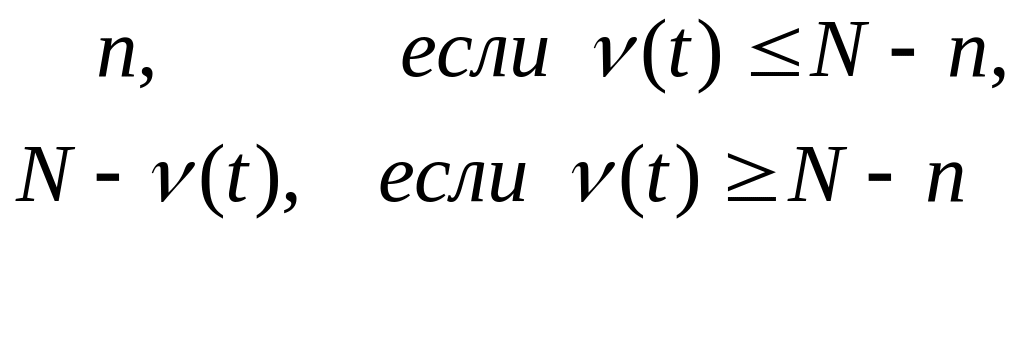
Отсюда легко получаются формулы для введенных коэффициентов:
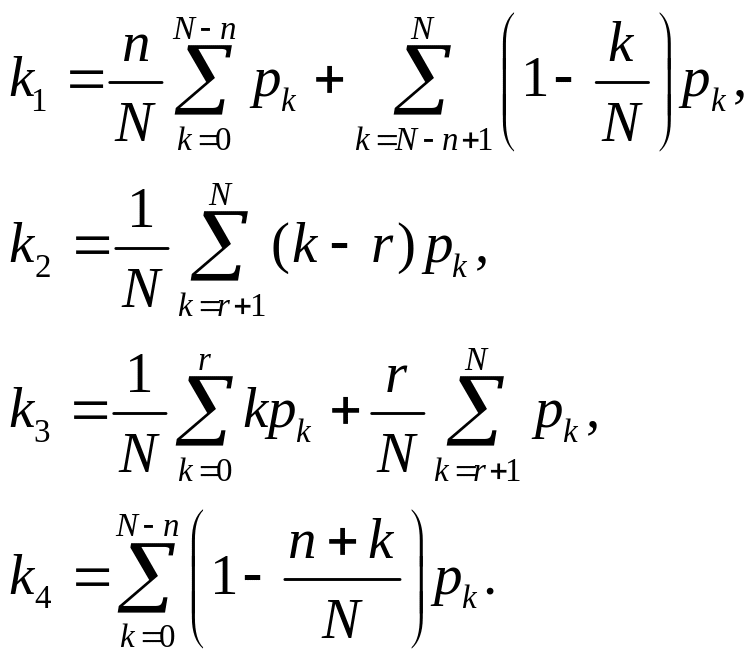(4.1)
Полученные коэффициенты характеризуют
качество резервной системы с
восстановлением. Например, большое
значение коэффициента
указывает на то , что ремонт идет медленно,
большое значение
говорит о том, что мало ремонтных единиц,
а большое число коэффициента
свидетельствует о том, что в системе
неоправданно большой резерв.
Реализация предложенного
выше подхода предполагает знание
вероятностей
нахождения системы в состояниях с
различным количеством отказавших
элементов i
. Аналитические методы оценки вероятностей
оказываются эффективными для моделей,
соответствующих схеме « гибели –
размножения» в предположении постоянства
интенсивностей перехода из одного
состояния в другое. Для иллюстрации
аналитического подхода рассмотрим
модельный пример. При анализе
технического обслуживания с НК
предположим, что в составе наземного
оборудования имеется пять устройств с
известными вероятностными характеристиками.
При проведении расчетов примем, что
время безотказной работы устройства и
время проведения ремонтных работ
подчиняется экспоненциальному закону
распределения . Кроме того будем считать,
что для выполнения целевой задачи
достаточно обеспечить безотказность
трех устройств из пяти и для восстановления
отказавших устройств используется один
ремонтный орган.
Граф состояний такой системы представлен на рис. 4.1
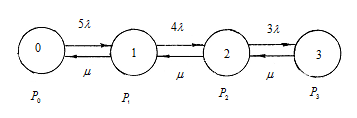
Рис. 4.1 Граф состояний обслуживаемой системы.
Согласно графу вероятности нахождения системы в различных состояниях будут удовлетворять системе дифференциальных уравнений Колмогорова. В стационарном режиме приходим к системе алгебраических уравнений
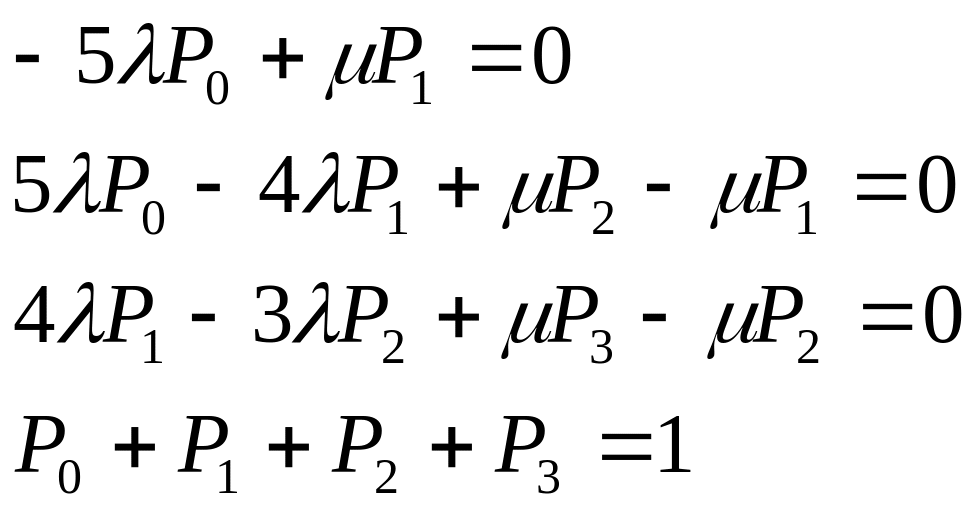
Соответственно в матричном виде получим
где
Отсюда
Расчеты проводились по программе Matchcad при следующих исходных данных
После подстановки исходных данных получим
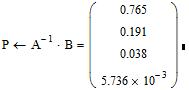
Показатели качества системы технического обслуживания рассчитывались по соотношениям ( 4.1 )
При записи этих выражений были приняты следующие обозначения:
;
;
;
Соответственно среднее число элементов находящихся в различных состояниях оценивается по соотношениям :
;
;
;
;
где
среднее число элементов, находящихся в рабочем состоянии;
среднее число элементов, находящихся в ожидании ремонта;
среднее число элементов, находящихся в ремонте;
среднее число элементов, находящихся в резерве.
Занятие №5
Задание
Оценить подтверждаемый уровень надежности по результатам измерений параметра работоспособности устройства ( см. табл. 1 ) Таблица 1.
№ варианта |
|
|
|
|
1 |
1,9 |
2,1 |
1,8 |
2 |
2 |
1,2 |
1,6 |
1,4 |
1,8 |
При проведении расчетов
считать: закон распределения параметра
принять нормальным; принять
,
где
уровень
доверительной вероятности;
соответственно
коэффициенты вариации действующих и
допустимых значений параметров.
Рассчитать подтверждаемый уровень надежности изделия по результатам утяжеленных испытаний ( см. табл. 2 )
Таблица 2
№ варианта |
Число испытаний , k |
Число отказов , k-d |
1 |
5 |
0 |
2 |
10 |
1 |
3 |
15 |
2 |
При проведении расчетов
принять :
2.
3. Оценить потребный объем испытаний k-го элемента системы при проведении автономных испытаний, оптимальный уровень надежности k-го элемента и коэффициент запаса, закладываемый на этапе его проектной разработки. Закон распределения параметра работоспособности элемента считать нормальным.
При проведении расчетов принять следующие исходные данные:
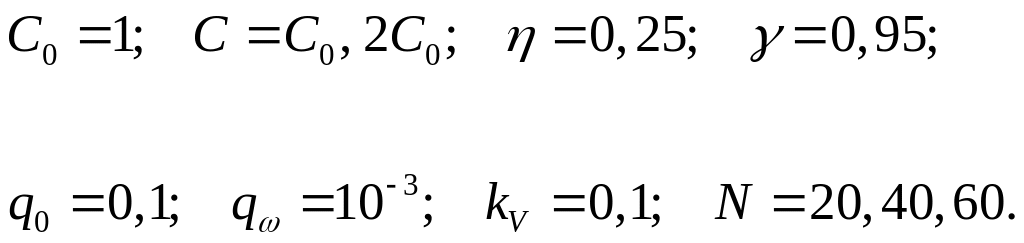
4. Оценить
потребные уровни коэффициента запаса
и объемы испытаний системы на этапе
наземной и летной отработки. При
проведении расчетов принять следующие
исходные данные :
коэффициенты вариации допустимых и
действующих значений параметров
При проведении расчетов законы распределения параметров принять нормальными.
5. Расчитать нижнюю границу доверительного интервала надежности
5.1
Число испытаний |
5 |
10 |
15 |
20 |
Число отказов |
1 |
3 |
5 |
7 |
5.2
Число испытаний |
5 |
10 |
15 |
20 |
Число отказов |
0 |
0 |
1 |
2 |
Задание №1
Расчет надежности представлен на рис 1.1.
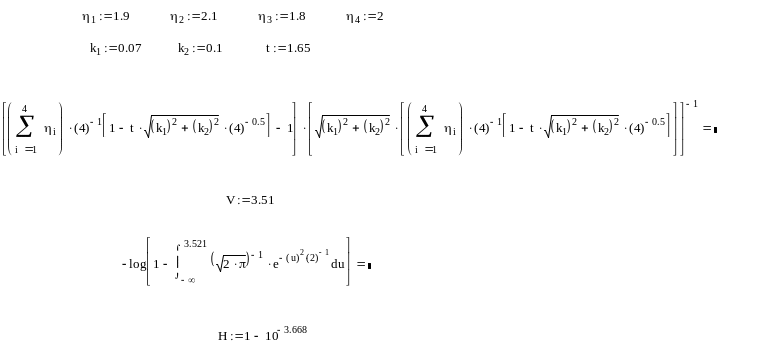
Рис. 1.1 Результаты расчета надежности.
Задание №2
Для иллюстрации рассмотрим численный пример. Допустим для рассматриваемого случая относительные разбросы параметра работоспособности будут равны
Утяжеленные испытания проводились с
коэффициентом
.
При десяти испытаниях произошел один
отказ. Задаваясь
,
по таблицам
находим :
.
Значения нижней границы доверительного
интервала надежности для
Число испытаний k |
Число отказов
|
|||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
5 |
0,55 |
0,34 |
0,19 |
0,08 |
0,01 |
|
|
|
10 |
0,74 |
0,61 |
0,50 |
0,40 |
0,30 |
0,22 |
|
|
15 |
0,82 |
0,72 |
0,64 |
0,56 |
0,49 |
0,42 |
0,40 |
|
20 |
0,86 |
0,78 |
0,72 |
0,66 |
0,60 |
0,54 |
0,50 |
0,44 |
Подставляя исходные данные в соотношение ( 9 ) , получим
.
Отсюда
2
0,966 = 1,932.
Таким образом, имеем
.
Заметим, что для подтверждения такого же уровня при испытаниях типа
«успех-отказ» потребовалось бы порядка десяти тысяч безотказных испытаний.
Задание №3
Зависимость стоимости от кратности резерва можно представить в виде
.
Вид
функции
зависит от типа резервирования .Очевидно,
в случае «горячего» резерва , имеем
.
В дальнейшем найдем аналогичные соотношения для элементов с параметрической избыточностью. При решении поставленной задачи, вероятность отказа элементов с параметрической избыточностью условно представим в виде
где
- вероятность отказа элемента,
соответствующая коэффициенту запаса
;
условная
кратность резерва.
Согласно
результатам, полученным в работе [ 7 ],
надежность элемента
,прогнозируемая
после проведении k
испытаний , может быть оценена по
соотношению
,
где
коэффициент
вариации коэффициента запаса;
уровень доверительной вероятности;
математическое
ожидание коэффициента запаса.
Знание , позволяет оценить условную кратность резерва
,
В
дальнейшем будем считать, что стоимость
резервированного элемента пропорциональна
коэффициенту запаса
.
Тогда функцию
можно оценить по соотношению
.
Характер изменения функции представлен на рис.
Характер изменения функции
для
элементов с параметрической избыточностью.
При построении графика было приняты следующие исходные данные:
1.3
;
0,95 ;
0,1 ;
2, 5, 10.
Как видно из графика функция слабо зависит от объема испытаний k . Приближенно для функции может быть принята линейная аппроксимационная зависимость
.
С учетом полученных результатов, выражение для стоимости примет вид
,
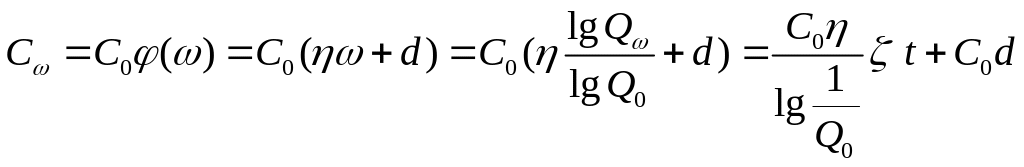где
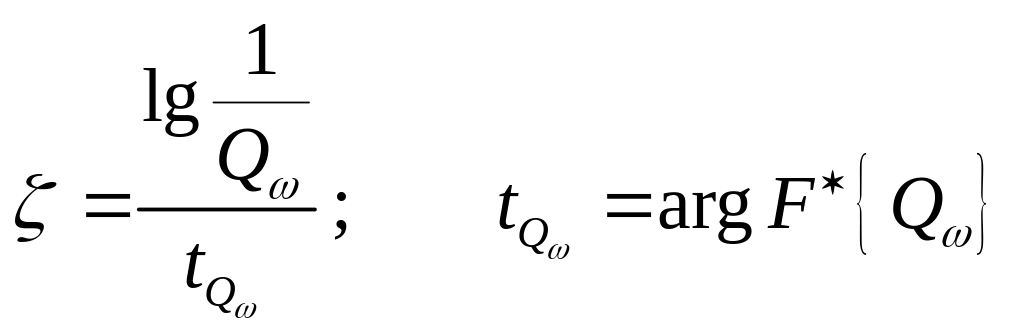
Отсюда
, где
.
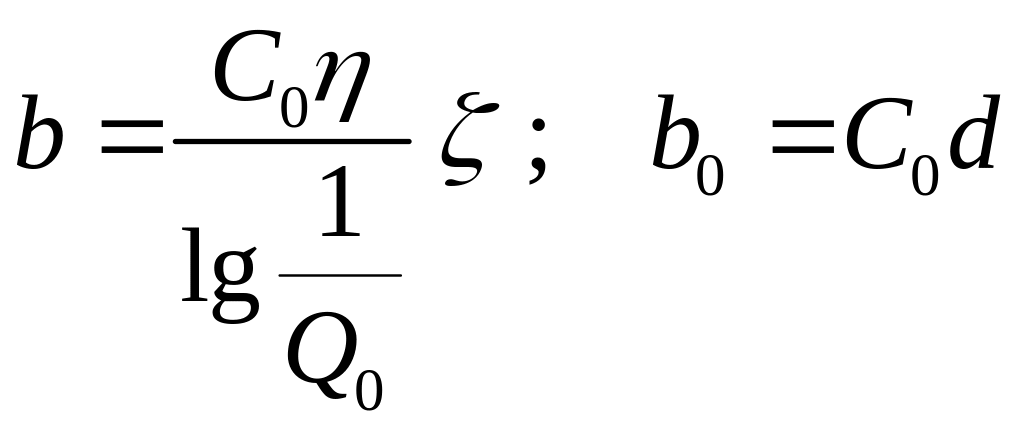N – объем выпускаемой
продукции;
коэффициент чувствительности,
характеризующий удельные затраты
на обеспечение единицы надежности, выраженной в гауссах.
Для
рассмотренного в примере случая :
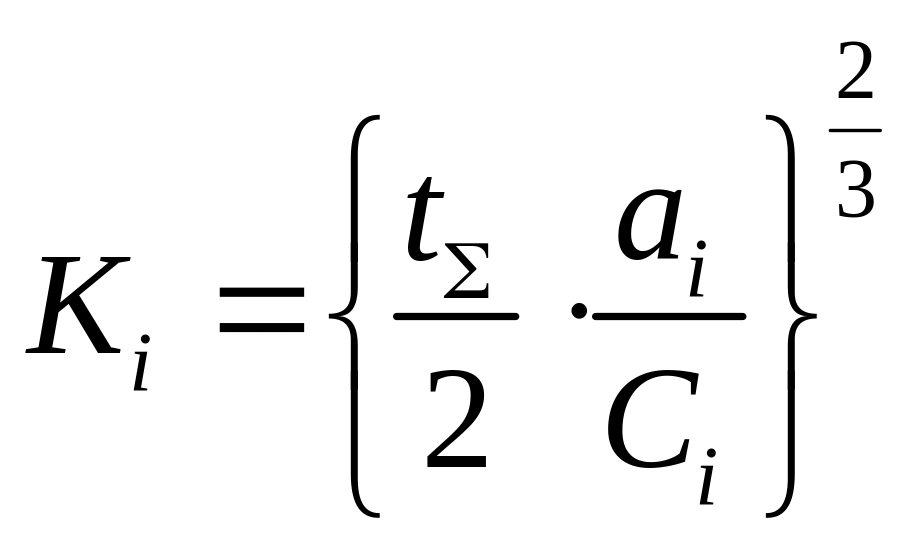
Соотношение позволяет оценить оптимальный
объем испытаний с точностью до целых.
Таким образом оптимальные объемы
испытаний отдельных элементов не зависят
от требований, предъявляемых к надежности
систем и определяются соотношением
удельных затрат на обеспечение единицы
надежности, закладываемой на этапе
проектирования,
и затрат на проведение одного испытания
.
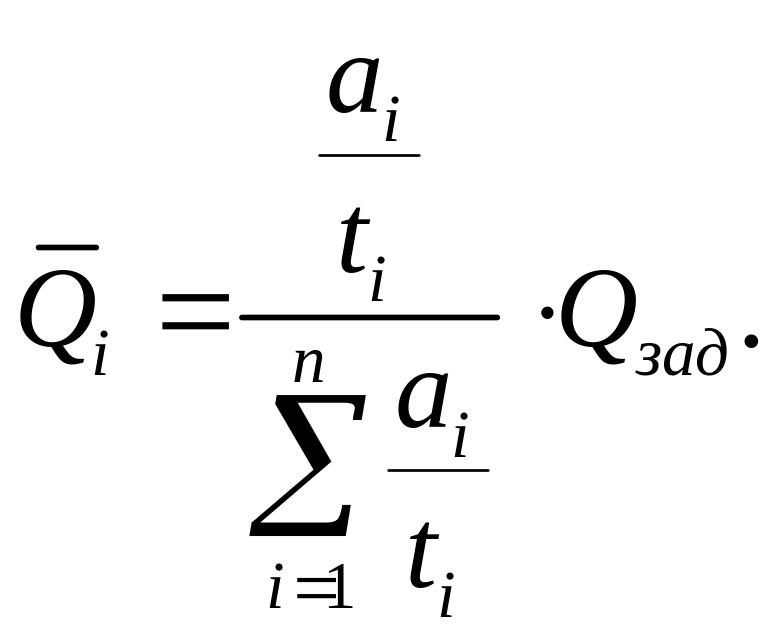
Таким
образом, оптимальные уровни вероятности
отказа пропорциональны удельным
затратам
и заданным требованиям к вероятности
отказа системы
.
.
, где
.
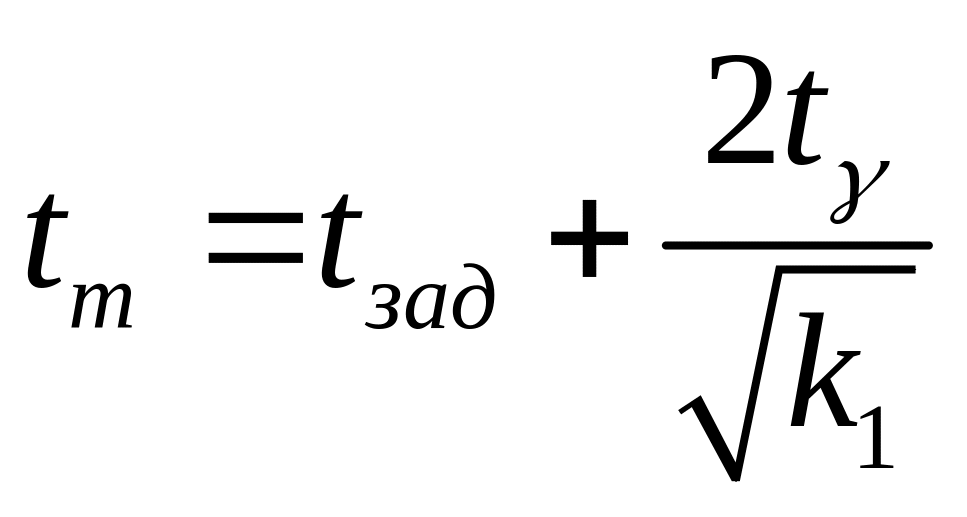Результаты расчета представлены на рис.3.1
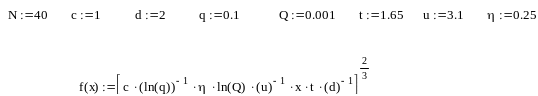
Рис. 3.1 Зависимость числа испытаний i-ой системы на этапе автономной отработки
от объема транспортной программы
(x=N).
Задание №4
При проведении ЭО могут встретится ситуации, когда измерения действующих и допустимых значений параметров происходит на различных этапах испытаний, в частности, на этапе стендовой отработки оцениваются допустимые параметры работоспособности системы, а на завершающем этапе испытаний измеряются действующие значения параметров. В этом случае стендовые испытания дают представление о ресурсах конкретных систем. Например, проводятся разрушающие испытания отсеков конструкции изделия, граничные испытания элементов системы управления на определение областей работоспособности систем и др. При этом случайный характер внешних воздействий может быть учтен только на завершающем этапе испытаний.
В дальнейшем допустим, что работоспособность
системы определяется параметром
.
Причем на этапе стендовых испытаний
оцениваются допустимые значения
параметров
,
а на завершающем этапе испытаний –
действующие значения
.
По результатам испытаний можно получить
точечные оценки математических ожиданий
этих параметров
и
.
Соответственно точечная оценка
коэффициента запаса
будет равна
.
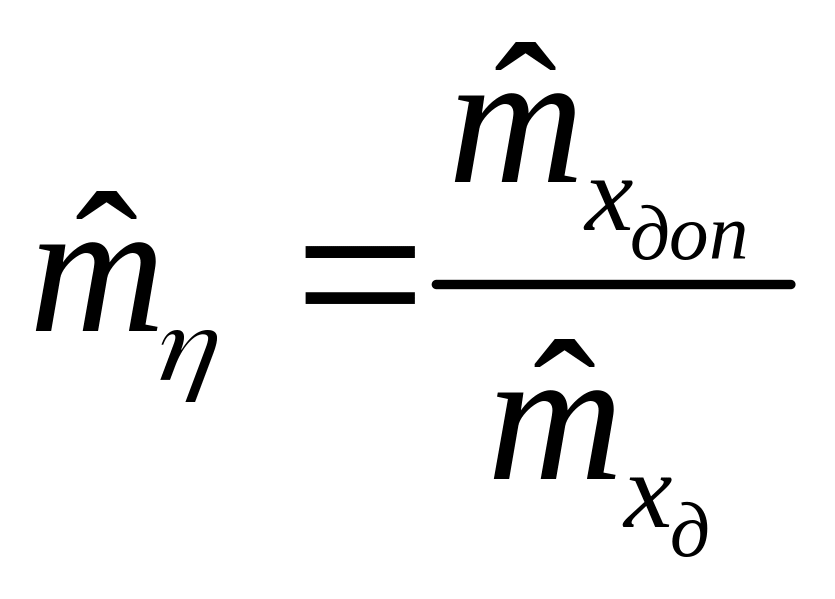В дальнейшем предположим, что
работоспособность устройства
обеспечивается при выполнении неравенства
.
Тогда, в случае нормального закона
распределения параметра
,
нижняя граница надежности
,
подтверждаемая при завершении ЭО, может
быть оценена по соотношению
,
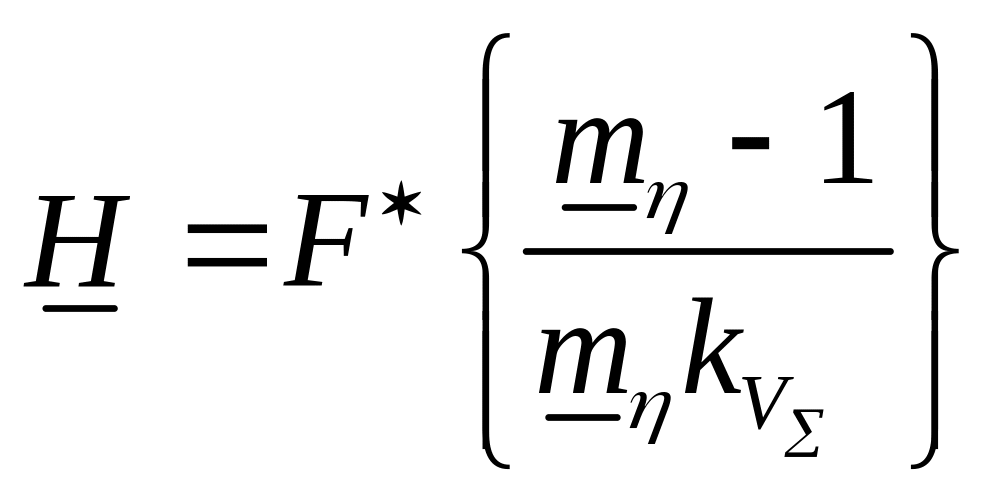где
;
нижняя граница одностороннего
доверительного интервала оценки
математического ожидания коэффициента
запаса
;
коэффициенты вариации соответственно
допустимых и действующих значений
параметров;
число испытаний соответственно при
проведении измерений допустимых и
действующих значений параметров ;
принятый уровень доверительной
вероятности ;
.
При планировании количества испытаний
на различных этапах ЭО воспользуемся
оценкой прогнозируемого уровня
математического ожидания коэффициента
запаса, потребного для обеспечения
заданных требований
к надежности устройства
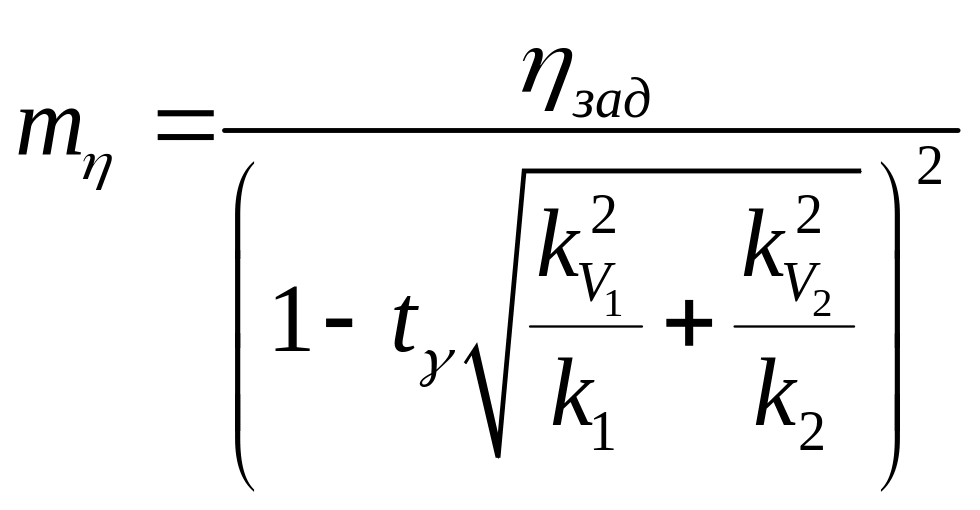, (2.55 )
где .
Как видно из соотношения ( 2.55 ) заданный
уровень надежности может быть обеспечен
при различных комбинациях значений
коэффициента запаса
и количества испытаний
и
.
Очевидно эти параметры целесообразно
задавать такими, чтобы соотношение (
2.20 ) выполнялось при минимальных затратах
средств. В общем случае суммарные затраты
на реализацию целевой программы можно
представить в виде
,
( 2.56 )
где
стоимости проведения одного испытания
соответственно при проведении стендовых
и завершающих испытаний ;
затраты на производство и эксплуатацию
изделия при выполнении целевой программы;
функция
потерь при отказах;
ущерб
при отказе системы на завершающем этапе
испытаний;
среднее
число отказов на завершающем этапе
испытаний.
Очевидно стоимость
будет зависеть от уровня избыточности
системы по определяющему параметру
, величина которого закладывается на
этапе проектной разработки. При заданном
уровне
дисциплинирующее условие ( 2.55 ) можно
представить в виде
В рассматриваемом случае функция Лагранжа будет равна
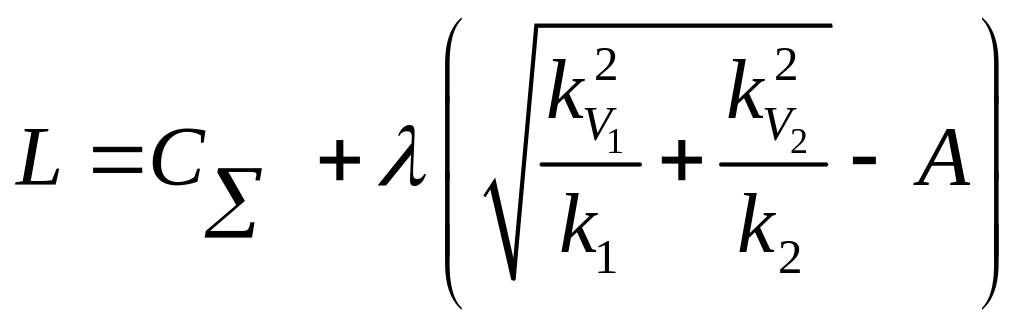
Таким образом оптимальные значения искомых параметров будут удовлетворять системе алгебраических уравнений
Раскрывая выражения для производных, получим
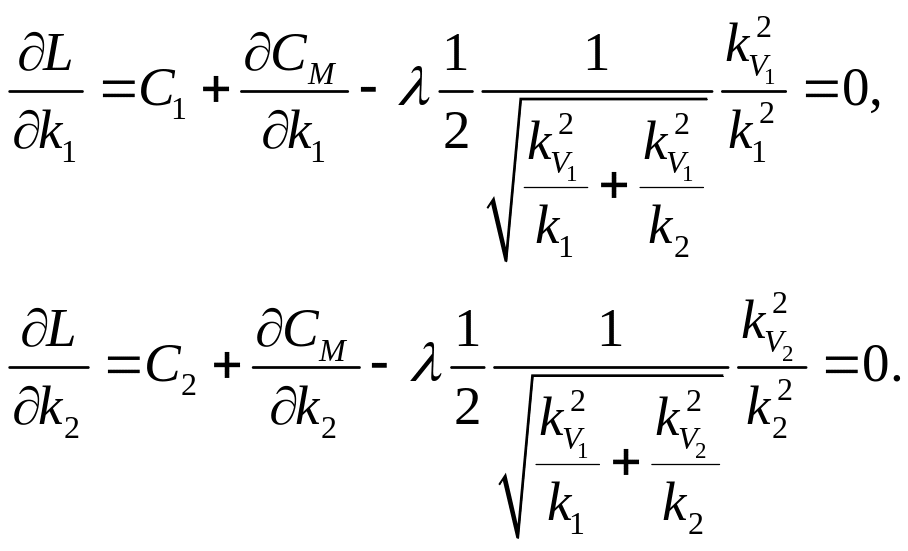
После преобразований, получим
,
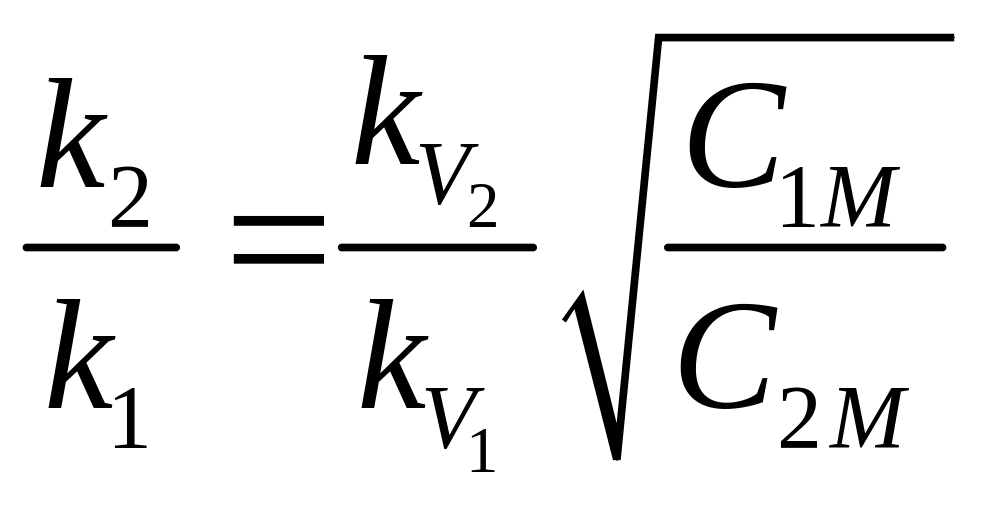( 2 57 )где
Таким образом оптимальное соотношение объемов испытаний на различных этапах ЭО не зависит от требований, предъявляемых к надежности
устройства , а так же не зависит от уровня его параметрической избыточности . С учетом соотношения ( 2.57 ) суммарные затраты будут равны
,
где
.
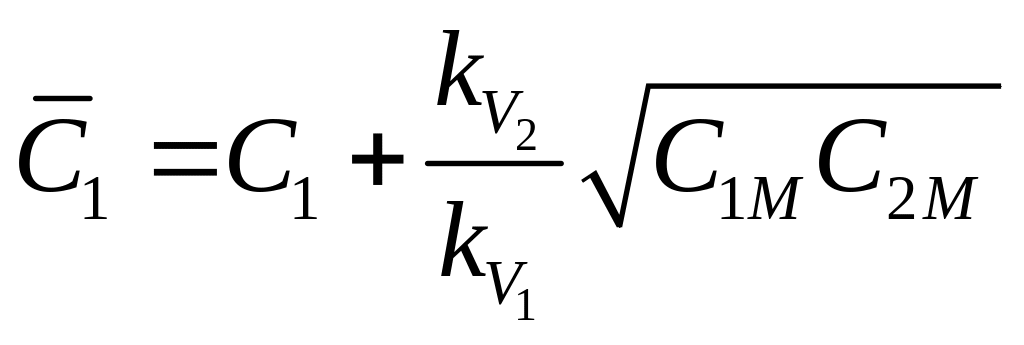Дисциплинирующее условие ( 2.55 ) в дальнейшем представим в виде
,
где
.
Подставляя выражение для из соотношения ( 2.57 ), получим
,
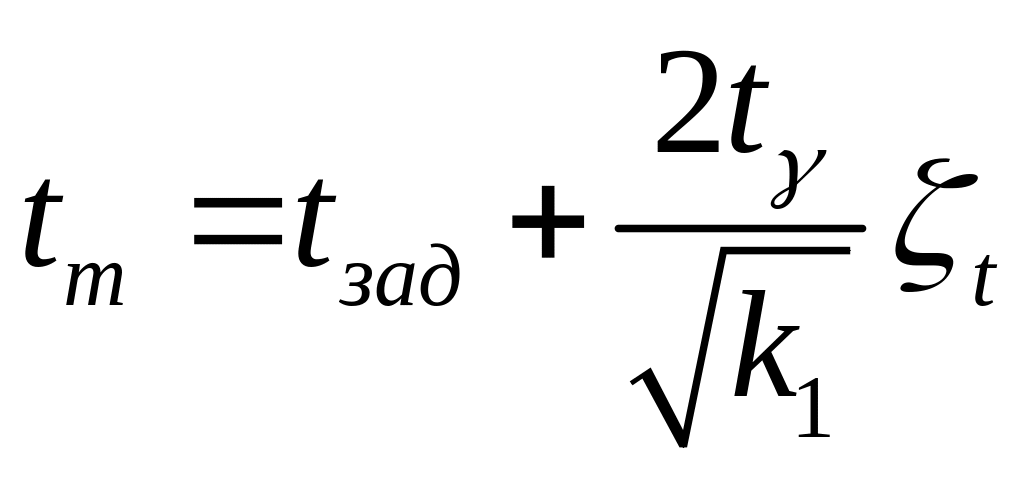( 2.58 )
где
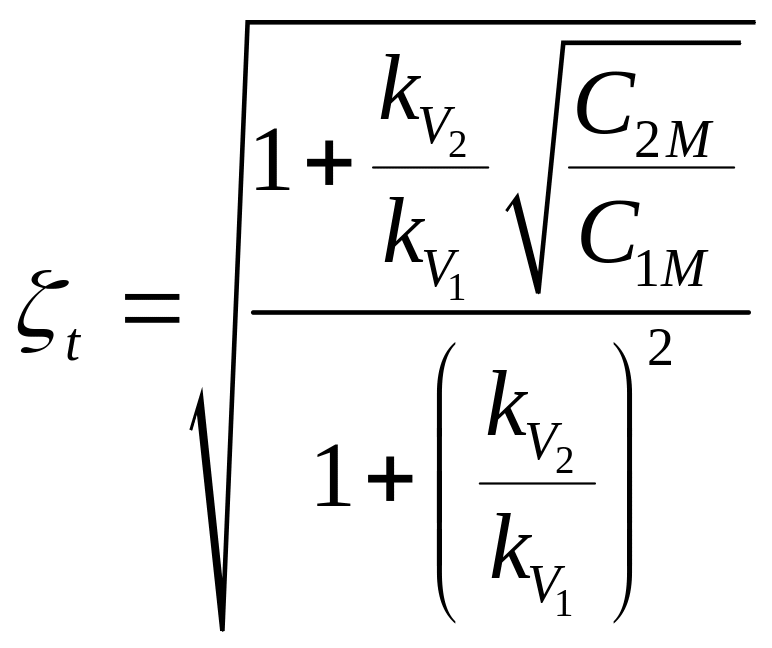
При оптимизации объема испытаний воспользуемся выражением для эксплуатационных затрат
,
где
.
В рассматриваемом случае условие
оптимальности примет вид
.
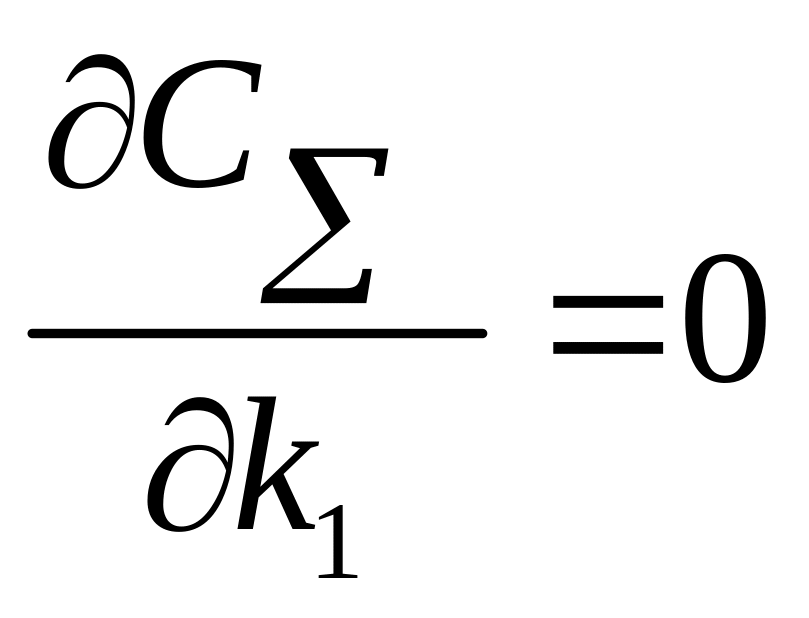Раскрывая выражение для производной, получим
.
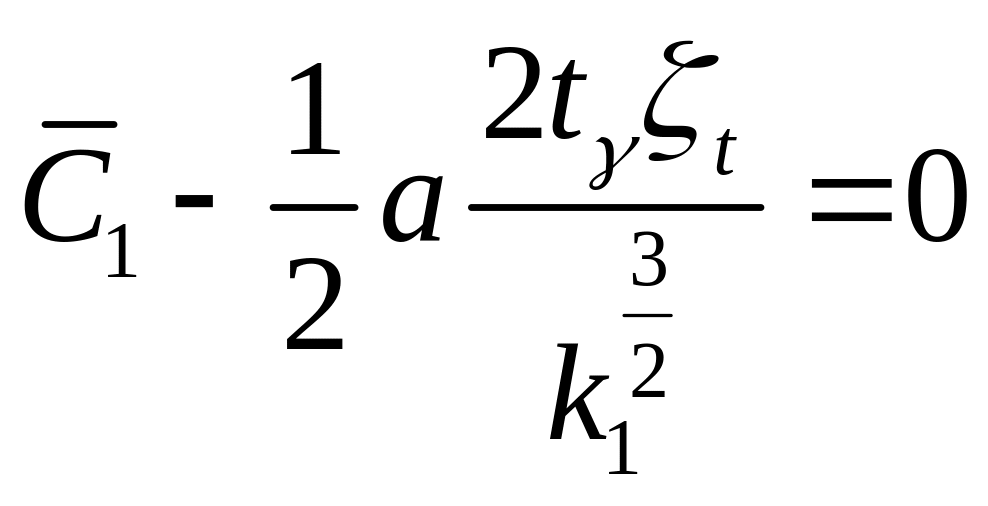Разрешая уравнение относительно , найдем оптимальный объем стендовых испытаний
.
(
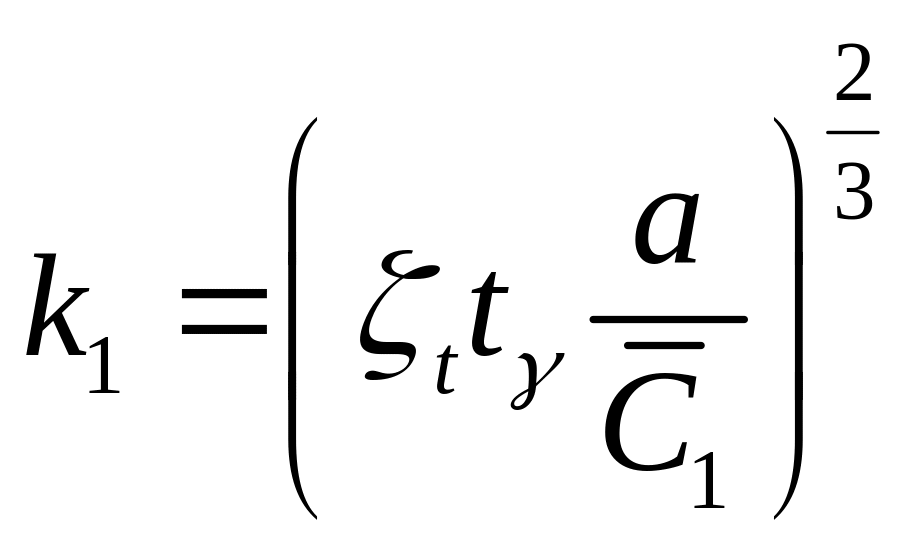2.59 )
Знание
позволяет оценить параметр
и соответствующий ему уровень избыточности
системы
, где .
При проведении расчетов первого
приближения значения производных
принимаются равными нулю. В этом
случае можно принять
.
В дальнейшем по соотношениям ( 2.57 – 2.59
) оцениваются оптимальные значения
параметров
первого приближения. В окрестности
полученного квазиоптимального решения
рассчитываются значения функции
,
где
вероятнть отказа при проведении первого
испытания на завершающем этапе отработки;
.
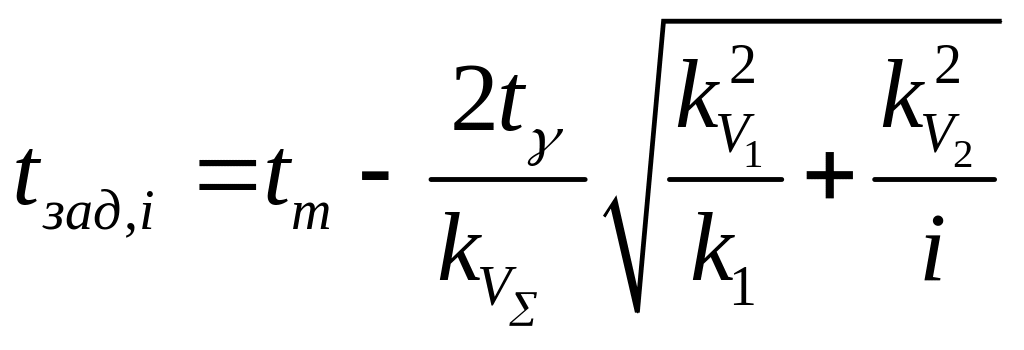Оценка производных
могут быть получены численно либо
графически.
В дальнейшем проводится итерационное уточнение квазиоптимального решения с учетом полученных значений производных.
Пример. Для иллюстрации предлагаемого
подхода рассмотрим модельный пример.
При проведении расчетов примем следующие
исходные данные :
При расчете первого приближения были получены следующие результаты:
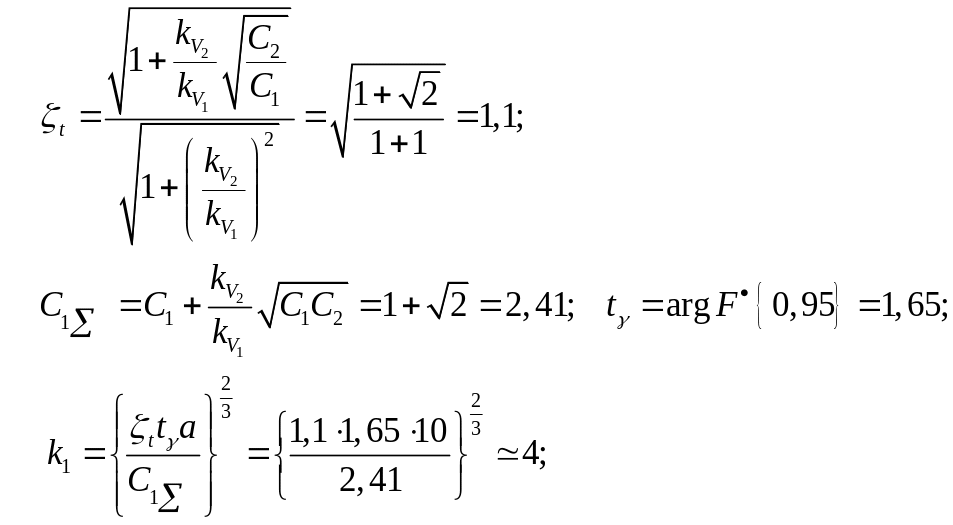
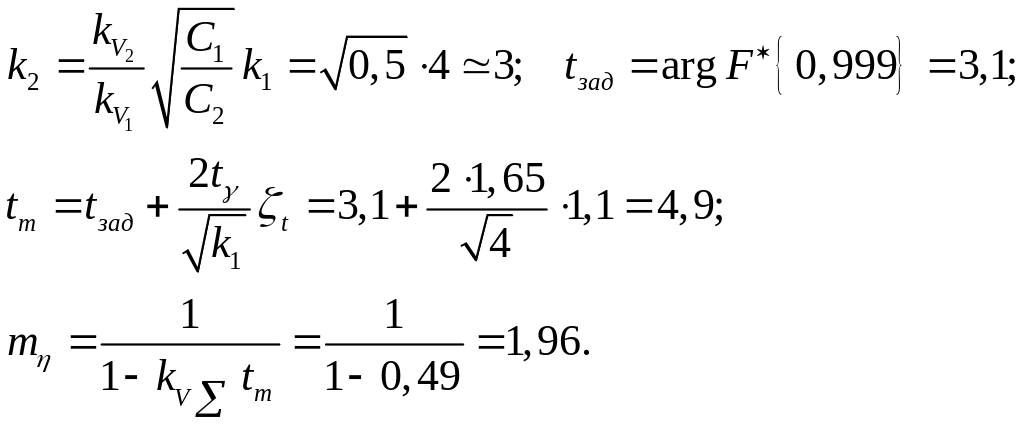
Результаты расчета представлены на рис. 4.1
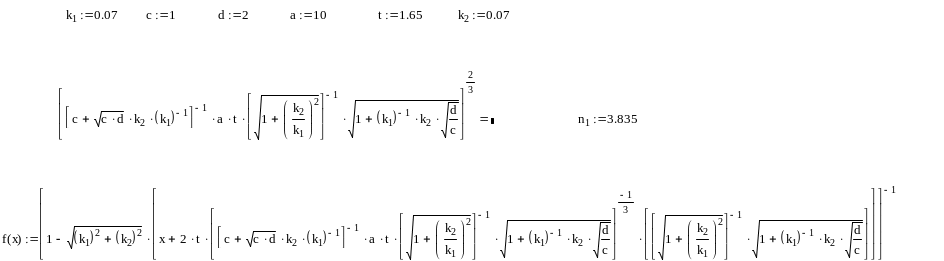
число
испытаний на этапе наземной отработки
.
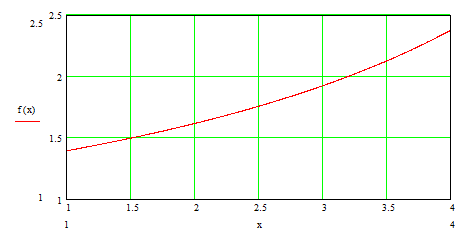
Рис.
4.1 Зависимость коэффициента запаса
от уровня подтверждаемой надежности
,
выраженной в белах.
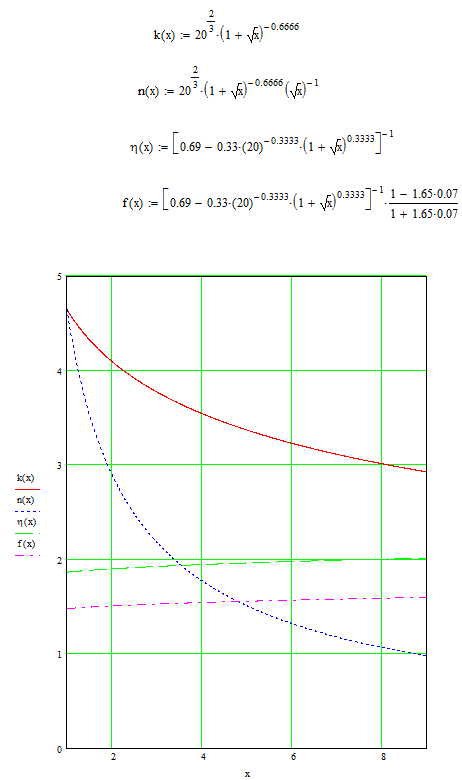
Рис. 4.2 Зависимость числа испытаний k на первом этапе ЭО, числа испытаний n на
втором
этапе ЭО, коэффициента запаса
и коэффициента безопасности f
от отношения затрат на проведение
одного испытания x=
,
соответственно на этапах летной и
наземной отработки конструкции.
Задание №5
Согласно (П.2.1), нижняя граница надежности является корнем уравнения
(П.2.2)
В
частности, для безотказных испытаний,
полагая d=n
, из соотношения (П.2.2) получим
.
Отсюда
(П.2.3)
Рассмотренный
метод позволяет производить оценки
надежности
отдельных элементов, входящих в состав
системы. Однако при решении практических
задач возникает потребность оценки
надежности системы в целом
при известных результатах испытаний
ее отдельных элементов. В дальнейшем
будем искать решение этой задачи для
систем с последовательным соединением
элементов. Строгое решение этой задачи
получено при проведении испытаний по
схеме «успех-отказ»
, (
П.2.4)
где
.
Следует заметить, что соотношение (П.2.4) является обобщением частного случая, соответствующего безотказным испытаниям
(П.2.5)
При других схемах проведения испытаний для нахождения интервальной оценки надежности системы используются приближенные методы.
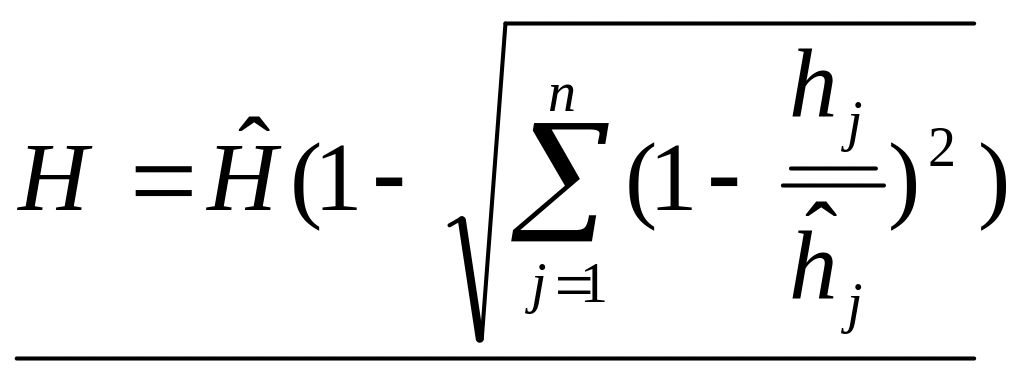
Значения нижней границы доверительного интервала надежности для
Число испытаний k |
Число отказов |
|||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
5 |
0,55 |
0,34 |
0,19 |
0,08 |
0,01 |
|
|
|
10 |
0,74 |
0,61 |
0,50 |
0,40 |
0,30 |
0,22 |
|
|
15 |
0,82 |
0,72 |
0,64 |
0,56 |
0,49 |
0,42 |
0,40 |
|
20 |
0,86 |
0,78 |
0,72 |
0,66 |
0,60 |
0,54 |
0,50 |
0,44 |
5.1
Число испытаний |
5 |
10 |
15 |
20 |
Число отказов |
1 |
3 |
5 |
7 |
|
0.8 |
0.7 |
0.666 |
0.65 |
|
0.34 |
0.4 |
0.42 |
0.44 |
=
0.025
Схема «успех-отказ» :
=
0.102
Общий случай:
=
0.03
5.2
Число испытаний |
5 |
10 |
15 |
20 |
Число отказов |
0 |
0 |
1 |
2 |
|
1 |
1 |
0.93 |
0.9 |
|
0.55 |
0.74 |
0.72 |
0.72 |
=
=0.21
Схема «успех-отказ»:
=
=0.46
Общий случай :
=
0.335
Занятие №6
Обеспечение надежности на этапе производства.
Задание
Оценить значения коэффициентов точности и сравнения для исходных данных, представленных на рис. 3
|
|
|
|
|
|
а) |
б) |
в) |
мм
мм
мм
мм
мм
мм
мм
мм
мм
мм
мм
ммРис. 3 Гистограммы и кривые выравнивающих частот толщины листов:
а) – листы 1,81500
из сплава АМг5ВН; б) – листы 3,02000
из сплава АМг3П; в) – листы 2,01200
из сплава АМцАМ (На графиках обозначено:
точечная
оценка математического ожидания
праметра,
точечная
оценка среднего квадратического
отклонения параметра.)
Оценить процент брака для следующих исходных данных:
МПа – математическое ожидание предела
прочности,
МПа - среднее квадратическое отклонение
предела прочности,
МПа - предел прочности материала по
ГОСТу.
Закон распределения параметра
-- нормальный.
3. Найти объем выборки n и приемочный уровень при контроле надежности по методу Неймана - Пирсона. При решении задачи принять следующие исходные данные:
1).
(
) (
)
(
)
2).
3).
.
4)
.
Закон распределения
нормальный.
4. Найти объем выборки и приемочный уровень при контроле продукции по методу Неймана – Пирсона. Решить задачу различения двух гипотез :
приемка
партии,
браковка партии.
МПа – математическое ожидание предела прочности,
МПа - среднее квадратическое отклонение предела прочности,
МПа - предел прочности материала по ГОСТу,
- риски поставщика и заказчика.
5.. Найти области приемки ( браковки ) при статистическом контроле надежности методом последовательного анализа. При проведении расчета принять следующие исходные данные:
.
(
)
(
)
Закон распределения
коэффициента запаса
принять нормальным. (
)
6. Оценить средний объем испытаний n при контроле надежности по методу Вальда (последовательного анализа) при нормальном законе распределения контролируемого параметра. При проведении расчетов принять следующие исходные данные:
.
7. Учет ошибок контроля в режиме применения.
Задание №1
Для исходных данных,соответствующих пункту a ), получим следующие характеристики процесса:
а)
;-
коэффициент сравнения,
;-поле
рассеивания параметра,мм
;-допуск,мм
-коэффициент
точности.
Задание № 2
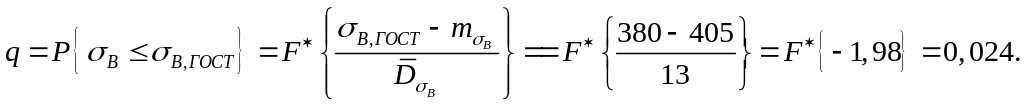
Задание
№3( 1) (
)
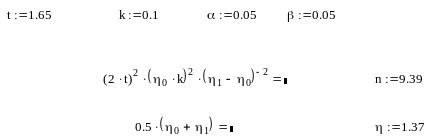
Задание №4
Результаты расчетов представлены ниже:
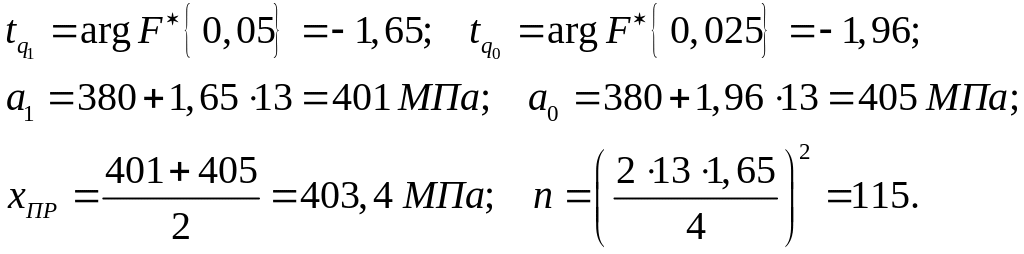
Задание №5
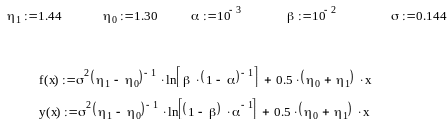
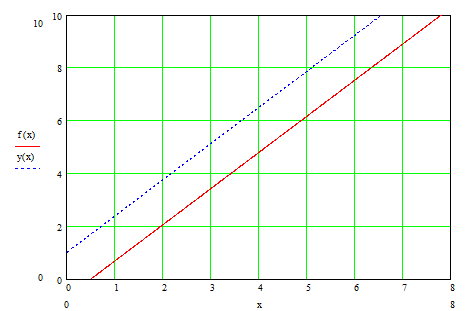
Рис. 1.1 Изменение границы подтверждения надежности y(x) и границы области отбраковки f(x) по числу испытаний x
Задание №6
Учет ошибок контроля в режиме применения.
Влияние ошибок контроля на характеристики работоспособности систем рассмотрим для систем с «холодным» резервом. При «холодном» резервировании используется несколько одинаковых элементов. Один из них работает, а другие находятся в состоянии ненагруженного резерва, ожидая включения, когда работающий элемент выйдет из строя.
В дальнейшем работоспособность
резервированной системы с учетом ошибок
контроля проанализируем на примере
системы с одним резервным элементом.
При проведении исследований примем,
что работающий элемент имеет вероятность
отказа
, а элемент, находящийся в резерве ,
отказывает с интенсивностью
.
В случае отказа оба элемента
восстанавливаются с интенсивностью
.
Вероятность пропуска отказа при
контроле
равна
.
Соответственно вероятность успешного
обнаружения отказа будет равна
.
В случае отсутствия ошибок контроля
отказавший элемент заменяется запасным
и система продолжает выполнять свои
функции. В случае возникновения ошибки
контроля замена отказавшего активного
элемента запасным не происходит и вся
система отказывает. Граф состояний
такой системы представлен на рис. 5.1.
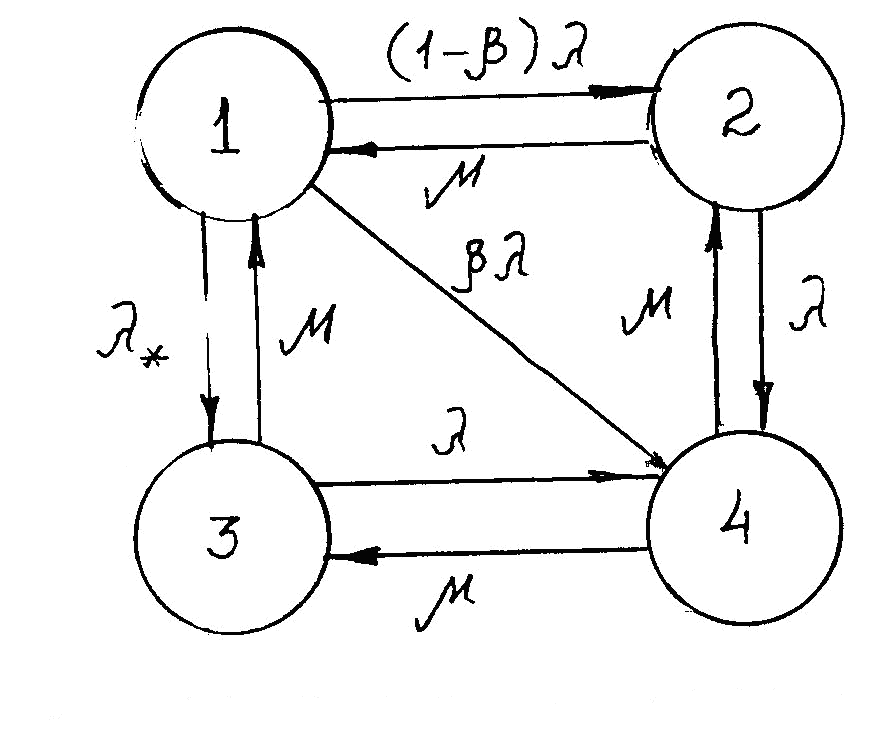
Рис. 5.1 Граф состояний системы с учетом ошибок контроля.
На графе первое состояние соответствует безотказности основного и запасного элементов. Второе состояние соответствует отказу основного элемента и подключению запасного. Третье состояние характеризует отказ запасного элемента и безотказную работу основного. Наконец, четвертое состояние соответствует ситуации, когда либо оба элемента отказали, либо отказал только основной элемент, а запасной не подключился к работе в виду ошибки контроля, что фактически означает отказ системы.
Согласно графу вероятности нахождения системы в различных состояниях удовлетворяют системе дифференциальных уравнений Колмогорова.
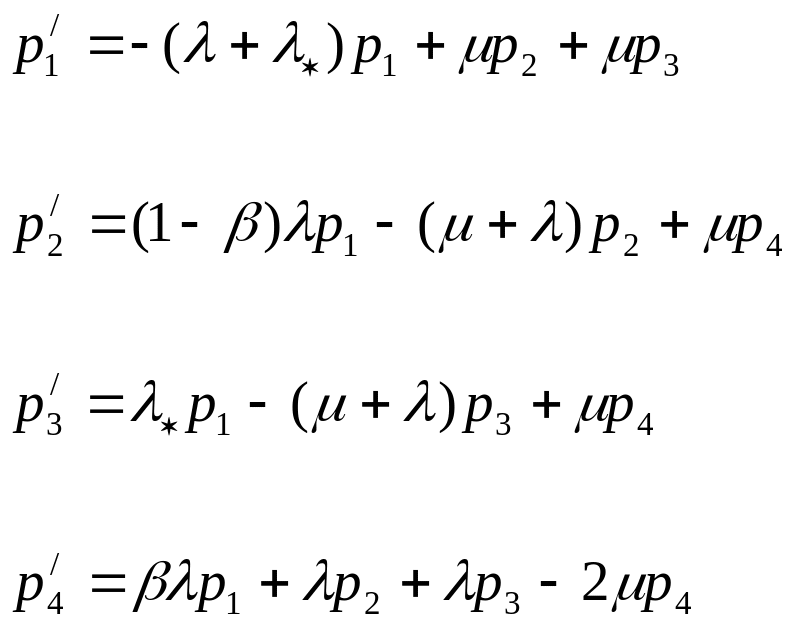(5.1)
В дальнейшем найдем среднее время работы
системы первого отказа. Для нахождения
среднего времени
пребывания системы в i
–ом состоянии воспользуемся
преобразованием Лапласа для вероятности
нахождения системы в этом состоянии
Переходя к пределу при
,
получим
Соответственно для производных получим
, где
,
( i=2,3,…n)
Применяя преобразование Лапласа к
уравнениям Колмогорова и переходя к
пределу при
, приходим к системе алгебраических
уравнений относительно
Знание
позволяет определить среднее время
работы системы до достижения любого
j-го состояния
.
Применяя преобразование Лапласа к обоим
частям системы (5.1) и производя предельный
переход, приходим к системе алгебраических
уравнений
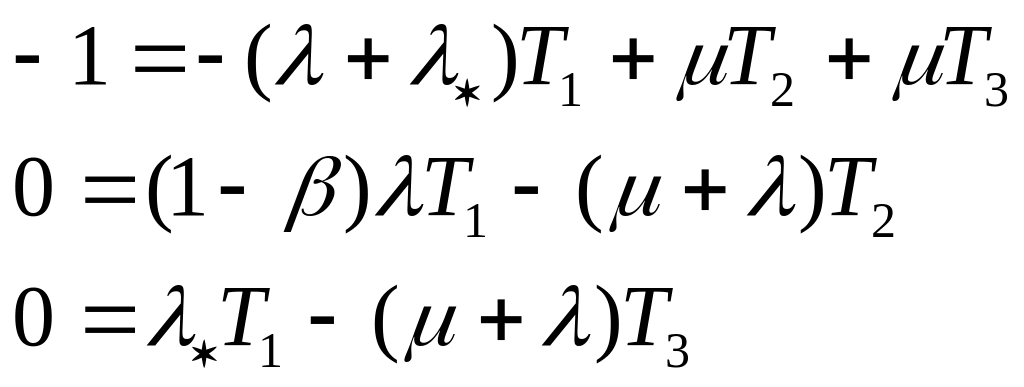(5.2)
В уравнениях значения характеризуют среднее время пребывания процесса в i—ом состоянии. Из второго и третьего уравнений найдем
Подставляя полученные выражения в
первое уравнение системы ( 5.2 ) и
производя преобразования, получим
Соответственно средняя наработка до первого отказа будет равна
(5.3)
Если интенсивность отказа резервного
элемента мала, можно принять
.
Тогда соотношение ( 5.3 ) упростится
Характер изменения
по
представлен на рис. 5.2 .При проведении
расчетов были приняты следующие исходные
данные:
;
.
Как видно из графика среднее время до отказа чувствительно даже к малым изменениям вероятности отказа при контроле .
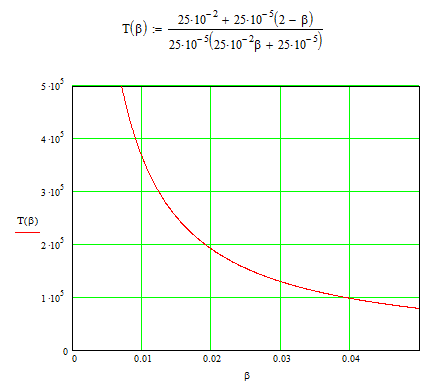
Рис. 5.2 Зависимость среднего времени до отказа системы от вероятности
ошибки контроля.
Занятие №7
Расчет числа отказов и обьема ЗИПа.
Задание
1. Рассчитать среднее число отказов и оценить гарантированный объем ЗИПа при
следующих исходных данных:
,
.
Привести ассинптотическую оценку
объема ЗИПа.
2. Привести график функции восстановления для случаев «горячего», «холодного» и общего резервирования.
3. Рассчитать средний срок службы трубопровода для следующих исходных данных:
(
)
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание №1
Задание №2
«Горячий» резерв
f(z)=
«Холодный» резерв
интенсивность всех переходов равна
;
;
Общий резерв
Граф переходов
переход происходит с интенсивностью
переход происходит с интенсивностью 3
Уравнения Колмогорова
=
f(z)
1-f(z)=
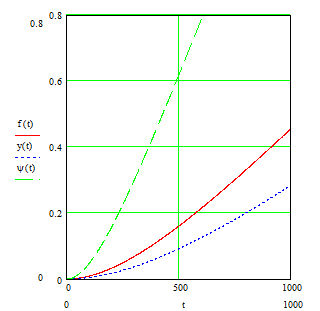
Рис.
2.1 Зависимость функции восстановления
от времени для «горячего» резерва
,
«холодного» резерва
и общего резерва
.
Задание №3
Результаты расчета представлены на рис. 1.1
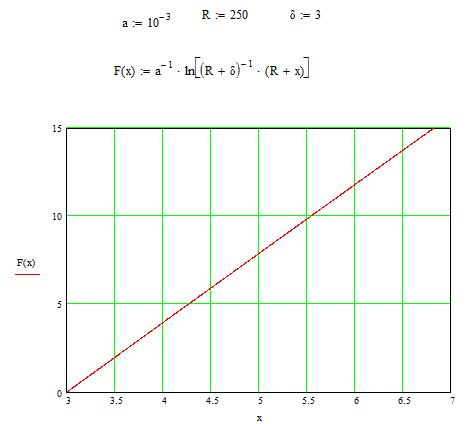
Рис.1.1
Зависимость срока службы трубопровода
в годах от толщины
трубы x=
в мм.
Занятие №8
Стратегии технического обслуживания.
Задание
1. Построить зависимость
упреждающего допуска
от периодичности обслуживания
( =0, 400, 800, 1200 ) для исходных данных, представленных в табл.1
Таблица 1
|
|
|
|
|
|
0,75
|
0,915
|
-0,0001
|
0,02
|
0,00002 |
200 |
(а)
(n)
(m)
(
)
(
2.Рассчитать периодичность
плановых замен для стратегии минимального
аварийного восстановления и различных
значений
.
Время безотказной работы подчиняется
закону распределения Вейбулла . (
)
.
3
Построить
зависимости периодичности замен от
параметра
для
для стратегии строго-периодического
восстановления и закона распределения
Вейбулла со следующими характеристиками:
.
4. Построить
график зависимости коэффициента
готовности
в режиме хранения от периодичности
и найти оптимальную периодичность
замен
при
различных значениях
5ч; 10ч; 30 суток; 100 суток и различных
уровнях интенсивностей отказа
Задание №1
Результаты расчета:
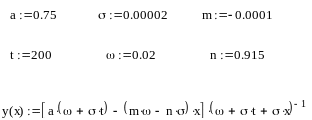
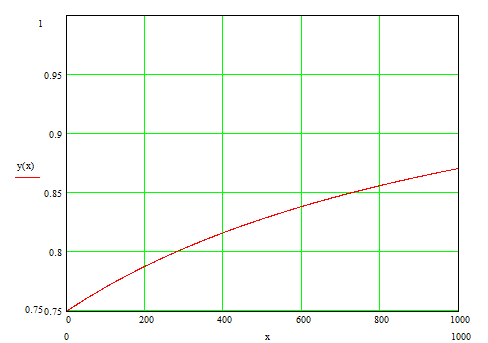
Рис. 1.1 Характер изменения
упреждающего допуска y(x)
от периодичности
замен
.
Задание №2
Результаты расчета представлены на рис.1.1
Рис.1.1 Зависимость
периодичности замен f(x)
в месяцах от параметра
.
Задание №3
Оптимальная периодичность замен находится по графику (рис.1.1) при удовлетворении условия:
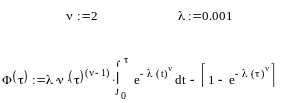
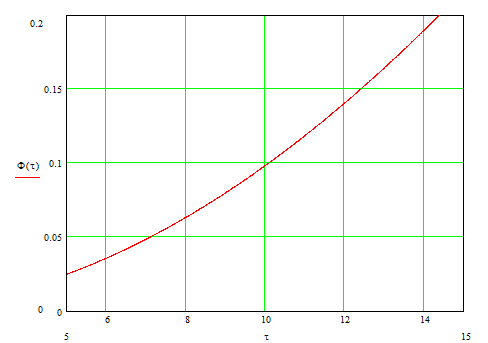
Рис.1.1 Зависимость
параметра
от периодичности замен
.
Задание №4
Результаты расчета коэффициента готовности представлены на рис.1.1
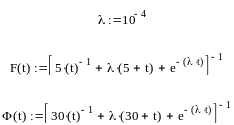
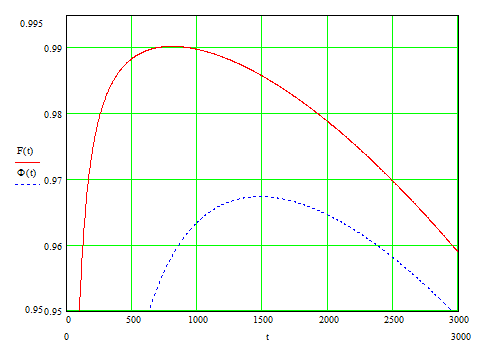
Рис. 1.1 Зависимость
коэффициентов готовности F(t)
при
и
Ф(t)
при
от периодичности обслуживания
.
ПРИЛОЖЕНИЕ
Использование метода максимального правдоподобия
в задачах обеспечения надежности технических систем.