
- •Методическое пособие по физике для студентов заочного факультета
- •Часть 1.
- •Содержание
- •§ 1. Механическое движение
- •§2. Радиус–вектор. Траектория. Путь. Перемещение
- •§ 3. Скорость
- •§ 4. Ускорение
- •§ 5. Угловая скорость и угловое ускорение
- •§ 6. Связь между линейными и угловыми величинами
- •§ 7. Первый закон Ньютона. Инерциальные системы отсчета
§ 3. Скорость
Как было отмечено выше, при движении частицы ее радиус–вектор в общем случае меняется как по модулю, так и по направлению. Для того чтобы охарактеризовать быстроту изменения положения точки, в кинематике вводят понятие скорости.
Пусть
частица движется по какой–либо
криволинейной траектории так, что в
момент времени
ей соответствует радиус–вектор
![]() .
В течение малого промежутка времени
.
В течение малого промежутка времени
![]() точка пройдет путь
и осуществит перемещение
точка пройдет путь
и осуществит перемещение
![]() .
.
Вектором
средней скорости
![]() называется отношение приращения
радиуса–вектора
к промежутку времени
:
называется отношение приращения
радиуса–вектора
к промежутку времени
:
![]() .
(3.1)
.
(3.1)
Направление вектора средней скорости совпадает с направлением . При неограниченном уменьшении средняя скорость стремится к предельному значению, которое называется мгновенной скоростью (или скоростью частицы в момент времени ):
![]() (3.2)
(3.2)
Таким
образом, мгновенная скорость есть
векторная величина, равная первой
производной радиуса–вектора движущейся
точки по времени. Поскольку секущая в
пределе совпадает с касательной, то
вектор скорости
![]() направлен по касательной к траектории
в сторону движения (рис. 3.1):
направлен по касательной к траектории
в сторону движения (рис. 3.1):

Рис. 3.1
По мере уменьшения путь все больше будет приближаться к , поэтому модуль мгновенной скорости
![]() (3.3)
(3.3)
Таким образом, модуль мгновенной скорости равен первой производной пути по времени.
С учетом выражений (2.9) и (3.2)
![]() (3.4)
(3.4)
где
![]() – проекции
вектора
на неподвижные координатные оси (орты
являются постоянными векторами). Таким
образом, проекция скорости на координатную
ось равна первой производной координаты
по времени.
– проекции
вектора
на неподвижные координатные оси (орты
являются постоянными векторами). Таким
образом, проекция скорости на координатную
ось равна первой производной координаты
по времени.
Модуль скорости
![]() (3.5)
(3.5)
В соответствии с формулами (2.10) и (3.1) элементарный путь, пройденный частицей за элементарно малый промежуток времени, равен
![]() (3.6)
(3.6)
Для
того чтобы определить путь
![]() ,
проходимый частицей за конечный
промежуток времени
,
следует проинтегрировать выражение
(3.6) по времени в пределах от
,
проходимый частицей за конечный
промежуток времени
,
следует проинтегрировать выражение
(3.6) по времени в пределах от
![]() до
до
![]()
 (3.7)
(3.7)
Очевидно,
что взятие определенного интеграла
(3.7) требует знания зависимости модуля
скорости от времени
![]() .
.
Пример
3.1. Радиус–вектор
частицы
![]() м.
Найти путь
частицы за одиннадцатую секунду ее
движения.
м.
Найти путь
частицы за одиннадцатую секунду ее
движения.
Решение. Путь, проходимый частицей за промежуток времени ,
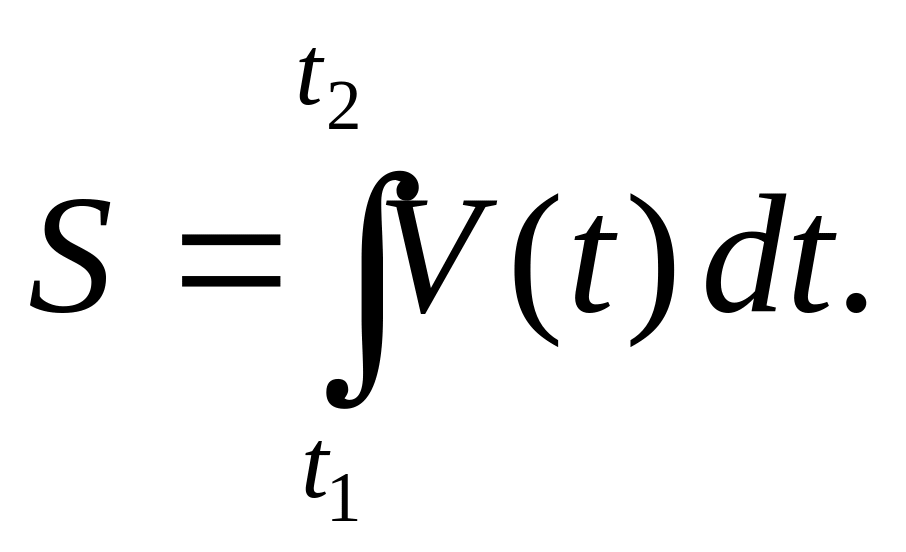 (3.8)
(3.8)
По
условию задачи
![]() =10
с,
=10
с,
![]() =11
с.
=11
с.
Найдем
зависимость модуля скорости
![]() от времени
от времени
![]() .
.
![]()
Модуль скорости частицы
![]()
Подставим
полученное соотношениее
![]() в выражение (3.8) и проинтегрируем:
в выражение (3.8) и проинтегрируем:

Подставляя численные значения и , окончательно получаем
![]() .
.
Ответ:
![]() .
.
