Абстрактная алгебра

Алгебраической операцией на множестве М называется отображение

φ : М ⁿ → М ( n –й декартовой степени множества М в само множество М). Число n называется арностью алгебраической операции. При n =2 операция называется бинарной ( любым двум элементам множества М ставится в соответствие один и только один элемент множества М).

Пример 1. Алгебраической операцией является

(отв.- умножение на множестве рациональных чисел)

Пример 2. Бинарной операцией на множестве R³ является

(отв. - векторное произведение (операция над двумя векторами)

Элемент е М называется нейтральным элементом относительно бинарной операции на множестве М, если для любого m М

е*m = m = m*е.

Пример 3. Бинарной операцией на множестве R² является

(отв. -

Пример 4. Нейтральным элементом относительно объединения множеств является (отв. – пустое множество)

Группой называют некоторое множество с заданной на нём операцией, причём для любого элемента группы существует обратный элемент.

Пример 5. Группой является множество

(отв. – множество рациональных чисел без нуля с операцией умножения)

Пример 6. Группу по сложению образует множество

(отв. – множество целых чисел)

Пример 7. Подгруппой группы невырожденных матриц по умножению является подмножество матриц С

(отв. -

Пример 8. Линейным отображением пространства трехмерных векторов на пространство двумерных векторов является

(отв. - φ ( ) = (х₁ – х₂ ; 2х₃ + х₂ ) )

Дифференциальная геометрия Кривизна плоской кривой

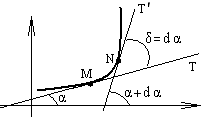Кривизной К кривой в её точке М называется предел отношения «угла смежности» δ между положитель-ными направлениями касательных в точках М и N к длине дуги , когда 0. = dS, = К = . Кривизна характеризует искривленность линии в рассматриваемой точке. Радиус кривизны кривой R = . Чем больше искривлена кривая вблизи данной точки, тем больше К и меньше R. Точки, в которых кривизна кривой равна нулю, называются точками распрямления кривой.

Пример. Уравнение кривой у = х ⁴ + 2 х ³ – 1. Имеем = 4 х ³ +6 х ² ; = 12 х ² +12 х. К = 0, когда числитель в формуле для кривизны кривой равен нулю, т. е. 12 х ² +12 х = 12 х (х + 2) = 0, откуда х ₁ = 0, х ₂ = - 2.Тогда у ₁ = 0, у ₂ = - 2. Следовательно, точки распрямления данной кривой (0; -1) и (- 1; - 2).

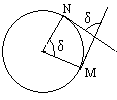Для окружности радиуса а кривизна К = = , R = а (постоянны во всех точках); для прямой К = 0, R = ∞; для прочих кривых К меняется от точки к точке.

Расчётная формула для кривизны К = .

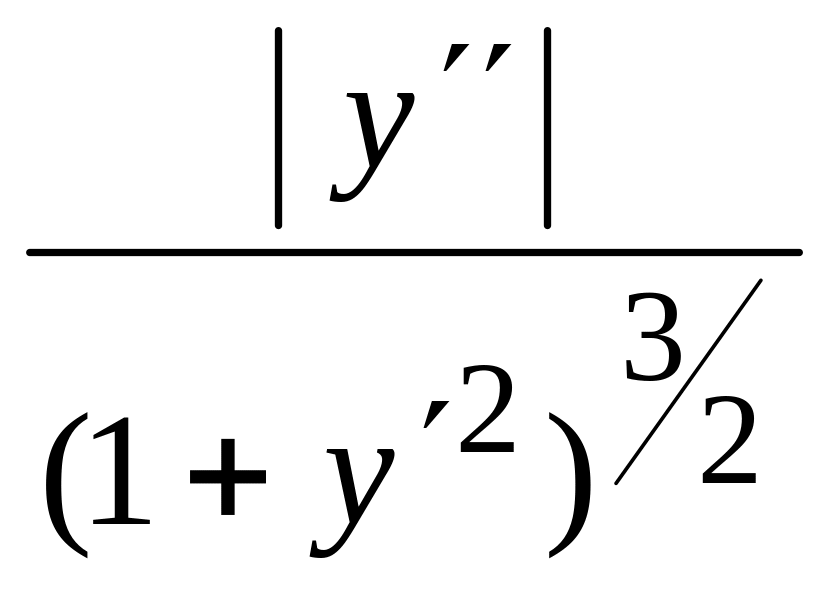Точки, в который кривизна кривой равна нулю, называются точками распрямления кривой.

Пример 1. Найти точки распрямления кривой у = х ⁴ + 2 х ³ - 1.

Решение. Имеем = 4 х ³ + 6 х ² , = 12 х ² + 12 х = 0, отсюда х ₁ = 0,

х ₂ = -1. Соответственно у ₁ = - 1, у ₂ = - 2. Точки распрямления данной кривой (0; -1) и ( -1; - 2).

Огибающей семейства F (х; у; z; с) = 0 называется геометрическое место точек, удовлетворяющих уравнениям .

Пример 2. Найти огибающую семейства х² + у² + (z – α)² – 1 = 0 (семейство сфер).

Решение. . Из второго уравнения z = α , а из первого имеем х² + у² =1. Следовательно, огибающей данного семейства является (отв. цилиндр круговой х² + у² =1, z = α.)

Граница множества – множество точек подпространства А топологического пространства Х, обладающих свойством, что любая окрестность каждой из них содержит как точки А, так и точки из Х \ А.

Пример 3. Границей множества М = {b} в топологическом пространстве Х = {а, b} с топологией t = {Ǿ, {а}, {а, b}} является ( отв. {b} )

Решение. Граничной точкой к множеству М называется точка, пересечение любой окрестности которой с М и с дополнением к М – не пусты. Таким образом, границей множества М = {b} в данном случае будет {b}.