Отображения (на примерах)

Пример 1. Пусть задано отображение f (х): х → (соs х; sin х ). Что представляет отображение f ([0; 2π)) ?

Решение. При х [0; 2π) функция соs х [-1; 1], sin х [-1; 1], причём соs ² х + sin² х = 1. Следовательно, отображение f ([0; 2π)) представляет собой окружность радиуса = 1 ( Отв. единичная окружность).

Пример 2. При отображении f (х ) = 2 tg х – 1 что является образом промежутка [0, ]?

Решение. Образом множества [0, ] при отображении f (х ) = 2 tg х – 1 являются те точки, в которые при данном отображении попадают точки отрезка [0, ].Так как [0, ] → [0, 1] (tg 0 = 0, tg = 1), то

отображение f (х )= 2 tg х –1 переводит исходный отрезок [0, ] в отрезок [-1; 1] ( Ответ: образ [-1; 1] )

Пример 3. При линейном преобразовании, заданном матрицей

А = 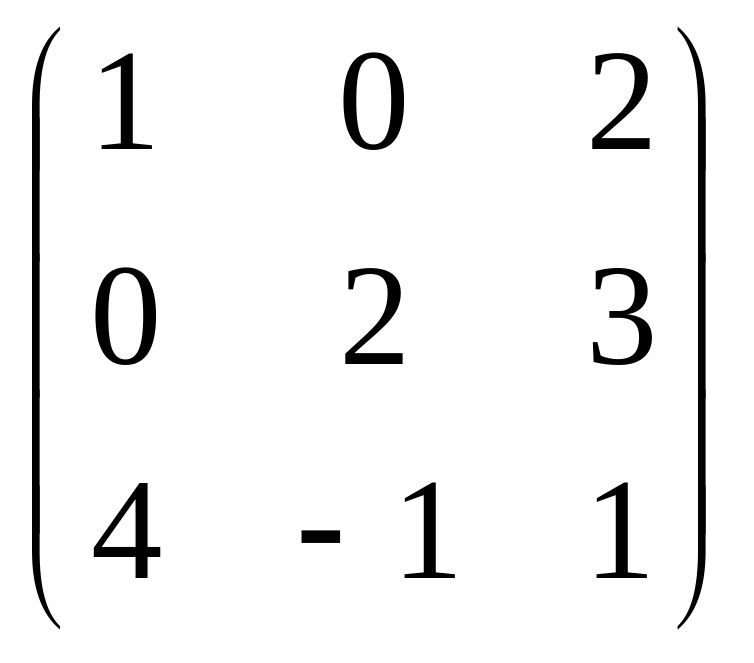, найти образ вектору .

Решение. Образ вектора определяется по формуле = А· =

= · = . ( ответ: )

Высказывания и операции над высказываниями.

Всякое утверждение, о котором имеет смысл говорить, что оно истинно или ложно, называется высказыванием.

Всякое высказывание либо истинно, либо ложно и не может быть одновременно истинным или ложным.

Алгеброй высказываний занимается специальная математическая дисциплина – математическая логика. В алгебре высказываний предполагается, что уже имеется некоторое множество высказываний, для каждого из которых известно истинно оно или ложно. Высказывания, входящие в это множество, называются элементарными (простыми). Элементарному высказыванию приписывают одно из двух истинностных значений – И или «единица», если оно истинно (достоверно), и Л или «нуль», если оно ложно. Из простых высказываний при помощи логических связок (союзов «и», «или»,слов «если…, то…», «тогда и только тогда, когда…», «если…,то…») образуются новые сложные высказывания. Истинность или ложность сложного высказывания полностью определяется, во-первых, тем, какие логические связки использованы для образования сложного высказывания, и, во-вторых, тем, какие из простых высказываний, образующих сложное, истинны и какие ложны.

Если высказывание образовано из двух высказываний при помощи союза «или», то говорят, что оно является суммой (дизъюнкцией) этих высказываний. Записывают в виде А + В или А В.

Если высказывание образовано из двух высказываний при помощи союза «и», то говорят, что оно является произведением (конъюнкцией) этих высказываний. Записывают в виде А ∙ В или А В.

Высказывание, образованное из двух высказываний при помощи союза «тогда и только тогда, когда…», «если…, о…»», называют соответственно эквивалентностью А В. или импликацией. Записывают в виде А В или А ~ В для эквивалентности, импликацию записывают в виде А В.

Истинность или ложность высказывания, образованного из каких-либо высказываний с помощью операций сложения, умножения, эквивалентности и импликации, зависит только от распределения истинности и ложности между высказываниями, над которыми производятся логические операции. Эту зависимость удобно описать следующими таблицами истинности логических операций

А	В	АВ
И И Л Л	И Л И Л	И Л Л Л

А	В	А В
И И Л Л	И Л И Л	И Л Л И

А	В	А В
И И Л Л	И Л И Л	И Л И И

А	В	А+В
И И Л Л	И Л И Л	И И И Л

Например, высказывание « х > 0 ». Его отрицание, т.е. равносильно « х ≤ 0 » и означает: неправда, что х положительно, а значит х ≤ 0