11

Дискретная математика

Множество – совокупность предметов (объектов, называемых элементами), объединенных некоторым общим признаком (свойством). Запись А = {х / х² – 3 х + 2 = 0} означает, что множеству А принадлежат все те элементы х, которые являются корнями уравнения х² – 3 х + 2 = 0, т. е. числа х = 1 и х = 2.

Бесконечное множество, элементы которого возможно занумеровать натуральными числами, называется счётным.

Множество всех рациональных чисел – счётное, а множество всех действительных чисел – несчётное.

Если любой элемент множества В принадлежит также множеству А, то множество В называется подмножеством множества А и записывают В А или А В. Например, всякое натуральное число (множество N) принадлежит множеству целых чисел (множество Z), т. е. N Z.

Из определения подмножества следует, что любое множество является подмножеством самого себя, т. е.справедливо утверждение А А.

Множество, состоящее из всех элементов, принадлежащих и множеству А и множеству В, называется пересечением множеств А и В и обозначается А В.

Множество, состоящее из всех элементов, принадлежащих или множеству А или множеству В, называется объединением множеств А и В и обозначается А В.

Обозначим через m (А) число элементов конечного множества А, тогда для любых конечных множеств А и В справедливо равенство

m (А В) = m (А) + m(В) – m(А В), если пересечение множеств А и В не пусто. Когда множества А и В не пересекаются, то m(А В) = 0 и

m (А В) = m (А) + m(В).

Разностью множеств А и В (дополнением множества В до множества А) называется множество всех тех и только тех элементов из множества А, которые не содержатся в множестве В, обозначается А \ В. Например, дополнением множества целых чисел до множества всех рациональных чисел является множество всех дробных чисел.

Пример 1. Даны множества А={- 3 < х ≤ 5}, В ={1 < х < 5}. Найти количество целых х .

Решение. Объединением множеств А и В является промежуток ( -3; 5], куда входит 8 целых чисел.

Пример 2. А = {20,30,40,50}, В = {20, 25, 30, 35}, С = {30, 35, 40, 45}. Найти число элементов множества Д = ( ) \ С .

Решение. = {20, 25, 30, 35, 40, 45, 50}. Множество Д = ( ) \ С содержит числа без чисел множества С, т. е. Д = {20, 25, 50}.

Пример 3. Даны множества А = {х : sin х = 0}, В = {х : 0 < х < 10}. Сколько элементов содержится в множестве А В ?

Решение. Множество А = {х : sin х = 0} = {х : х = πk, k Z}.

А В = {π; 2π; 3π}, следовательно, в нём 3 элемента.

Прямым или декартовым произведением множеств А и В называется множество упорядоченных пар (а, b), в котором а А, b В, т. е.

А × В = {(а, b) / а А и b В}.

Плоскость в выбранной прямоугольной системой координат изображает произведение множеств R×R (иногда пишут R² ).

Пример 4. Дано множество А = {2, 3, 4, 5, 6, 7, 8, 9} и бинарное отношение Р = {х, у / х, у А, х ≤ 3 }, причём х делит у без остатка. Найти количество элементов предиката (неопределённое высказывание – подмножество множества А)

Решение. Так как множество А состоит из 8 элементов, то декартово произведение А × А будет содержать n = 8 · 8 = 64 парных элемента. Предикат Р является подмножеством множества А × А . Нужно из 64 парных элементов выбрать только те, которые удовлетворяют условиям нашего предиката, т. е. первый элемент пары не должен быть больше 3, а второй должен делиться на первый без остатка . Тогда это предикат

Р = {(2; 2), (2; 4), (2; 6), (2; 8), (3; 3), (3; 6), (3; 9)}, который содержит 7 элементов. ( Ответ: 7 элементов. )

Мера плоского множества есть площадь соответствующей фигуры

П ример1.

S = π r₂ ² - π r₁ ² = π (4² – 2² ) = 12π.

П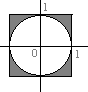 ример 2. Найти меру плоского множества А \ В, где

А { (х, у) R² : mах (| х |, | у | <1} и

В{ (х, у) R² : х ² + у ² <1}.

S = площадь квадрата минус площадь круга = 4 – π.

( ответ: 4 – π )

Пример3. Найти меру плоского множества { (х, у) R² : < у < 2,5 - х}. В начале находим точки пересечения линий, решая совместно систему уравнений у = и у = 2,5 – х. Имеем = 2,5 – х или 2х ² – 5х +2 = 0.

Отсюда х₁ = 2, х₂ = 0,5.

S = =

2,5 (2 – 0,5) – 0,5 (4 – 0,25) – ln 2 + ln 0,5 = - ln 4.

(ответ - ln 4 )

Пример 4. Найти меру плоского множества { (х, у) R² : х² + у² = 1}.

Так как множество состоит только из точек кривой – окружности, то мера данного плоского множества равна нулю. (Ответ: нуль )

Если по какому-то правилу каждому элементу х А ставится в соответствие определенный элемент у В, то такое соответствие называется отображением множества А в множество В и пишут f : А → В.

Символ f обозначает правило заданного соответствия. Это правило можно обозначать и другими символами.

Отображение, в котором различные элементы входного множества А соединяются с различными элементами выходного множества В и нет неприсоединенных элементов, называется биективным или взаимно однозначным соответствием.

Линейным отображением называется отображение φ, удовлетворяющее условиям φ (х + у) = φ (х) + φ (у); φ (λ х) = λ φ (х).

Отображение f : Х → У называется обратимым, если существует

f ^-1 : У → Х такое, что f ○ f ^-1 = е _х , f ^-1 ○ f = е _у , где е _х , е _у - тождественные отображения на множества Х и У соответственно.