Тема 5. Парная линейная регрессия

Виды регрессии: - парная y = f(x)

- множественная (зависит от множества факторов)

y = f(x₁, x₂, x₃ … x_n)

Большинство эконометрических моделей можно свести к парной регрессии, поэтому она получила широкое распространение.

Парная регрессия

Порядок распространения связи при парной регрессии:

1. Теоретическое обоснование связи.

Регрессия может быть парной, если существует доминирующий фактор, который влияет на результат у = у_х + ε

у_х – теоретические частоты;

ε – ошибка (возмущение).

Существует три рода ошибок:

1) Ошибки спецификации модели

Неверно подобрана функция или её параметры.

Методы устранения: оценка нескольких функций и выбор наилучшей.

2) Выборочный характер исходных данных

Совокупность исходных данных может быть неоднородна, тогда МНК не имеет смысла, т.к. он основан на расчете дисперсий. Поэтому из данных исключают наиболее выдающиеся в ту или иную сторону.

Методы устранения: расчет доверительных интервалов.

3) Особенности измерения переменных

Например, доход на душу населения не является точным, т.к. отсутствуют данные о сокрытых доходах.

Методы устранения: досчет на основе выборочных обследований; совершение операций сбора данных.

При анализе данных считают, что они однородны и точны, т.е. ошибки 2 и 3 рода устранены. Поэтому, уделяют наибольшее внимание устранению ошибок спецификации, т.е. подбору наиболее подходящего уравнения у_х. Цель этого отбора – уменьшить ошибки.

2. Выбор математической функции.

Осуществляется 3 методами:

А) графический

Б) аналитический

В) экспериментальный (по min остаточной дисперсии)

!Если остаточная дисперсия одинакова для нескольких функций, то выбирают наиболее простую.

! Каждый параметр при х должен рассчитываться по 6-7 наблюдениям.

Легче всего поддаются интерпретации линейные модели, тем более они требуют меньшего числа наблюдений, поэтому линейные модели изучают подробно, а нелинейные – подлежат линеализации.

Парная линейная регрессия

1. Вид: у = а + bх + ε

ε – ошибка спецификации.

2. Графическая интерпретация МНК

Рисунок 1.

Т.е. находим min ∑(у_i - y_ix)

Если разделим верхнюю часть на n, то:

- альтернативный метод расчета дисперсии

3. Интерпретация параметров a и b

b – коэффициент регрессии, показывающий на сколько в среднем изменилась функция, если изменить фактор на одну единицу.

а – значения функции при х = 0. Он не имеет экономического смысла, если оно отрицательно или х ни при каких условиях не равно 0.

Если а > 0 – вариация результата меньше, чем вариация фактора.

Если а < 0 - вариация результата больше, чем вариация фактора.

4. Измерение тесноты связи

Существует коэффициент парной линейной регрессии:

Если b > 0, то r > 0.

Если b < 0, то r < 0.

Если r ≈ 0 √ связи нет,

√ связь нелинейная.

5. Оценка качества модели

1. Осуществляется с помощью коэффициента детерминации:

Показывает, сколько процентов вариации у вы объяснили в вашей модели.

2. Критерий Фишера:

Показывает на сколько вся модель статистически значима в целом.

3. Стандартные ошибки в уравнении регрессии

- стандартная ошибка ля параметра b.

Она зависит от Х. Они применяется для проверки существенности коэффициента регрессии b и расчета его доверительных интервалов.

Существенность:

Если критерий Стьюдента меньше табличного при заданном значении степеней свободы, то гипотеза о несущественности параметра b принимается.

Для прогнозирования используют интервальные значения параметра b, т.е. доверительные интервалы: b ± t · m_b

t – табличное значение критерия Стьюдента.

Стандартная ошибка для параметра а:

t_a сравнивается с табличным значением при (n-2) степеней свободы.

- критерий Стьюдента

Т.о. проверка гипотез о значимости коэффициента регрессии и коэффициента корреляции проводится одинаково. Если коэффициент регрессии значимый, то коэффициент корреляции значимый.

6. Интервалы прогноза по уравнению регрессии

Чтобы понять, как определить величину стандартной ошибки, подставим в уравнение регрессии значение параметра а.

у_х = а + bх

Заменим значение у_х, и b на значение их ошибок и получим:

Из теории выборки известно, что средняя ошибка выборки:

Используем вместо дисперсии σ² остаточную дисперсию на 1 степень свободы:

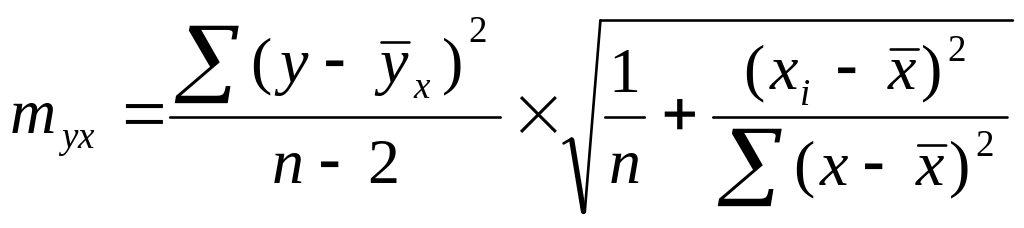
Х_i - прогнозное значение фактора Х, при котором мы хотим получить значение У.

у_х ± t · m_ух – формула для прогнозного значения У.

t – коэффициент Стьюдента при заданной степени вероятности.

В таблице приведены данные о потреблении и заработной плате по нескольким регионам Уральского Федерального округа.

Х – заработная плата;

У – потребление.

Задание: 1) выровнять модель методом линейной регрессии;

2) оценить надежность модели;

3) измерить тесноту связи и дать интерпретацию коэффициентам;

4) оценить уровень потребления при заданной заработной плате 65,0.

Таблица 1.

№ п/п	у	х	у·х	х2	у2	ух	у-ух	(у-ух)2	А
1	68,8	45,1	3102,9	2034,0	4733,4	61,5	7,3	53,1		96,0
2	61,2	59,0	3610,8	3481,0	3745,4	56,4	4,8	23,3		3481,0
3	59,9	57,2	3426,3	3271,8	3588,0	57,0	2,9	8,2		3271,8
4	56,7	61,8	3504,1	3819,2	3214,9	55,3	1,4	1,9		3819,2
5	55,0	58,8	3234,0	3457,4	3025,0	56,4	-1,4	2,1		3457,4
6	54,3	47,2	2563,0	2227,8	2948,5	60,7	-6,4	41,4		2227,8
7	49,3	55,2	2721,4	3047,0	2430,5	57,8	-8,5	71,8		3047,0
Итого	405,2	384,3	22162,3	21338,4	23685,8			201,8
Ср.знач.	57,9	54,9	3166,0	3048,3	3383,7			28,8

1) Уравнение линейной регрессии у = а + bх

Вывод: потребление уменьшится на 0,37, если заработная плата увеличится на одну единицу.

Вывод: если а > 0, то вариация результата меньше вариации фактора.

а = 78,21% - уравнение регрессии ненадежно.

2) Оценим надежность модели и тесноту связи

Вывод: связь обратная, средняя. Совпадает связь при r и b.

3) Оценим качество модели

Рассчитаем ошибку аппроксимации и коэффициент детерминации

4)Рассчитаем среднюю ошибку аппроксимации

5) Рассчитаем критерий Фишера

Вывод: чем больше F_факт, тем надежнее уравнение.

m – количество переменных при х = степени свободы числителя.

n – количество измерений.

m-n-1 – степень свободы знаменателя.

Для σ²_у соответствует степень свободы, равная (n-1).

Для σ²_{объяснен.} соответствует степень свободы, равная m.

Для σ²_ост. соответствует степень свободы, равная (n-m-1).

Если регрессия линейная, то n-1=1+(n-1-1)

n-1=1+(n-2)

Критерий Фишера представляет из себя таблицу.

Фрагмент таблицы: при ά = 0,05

К1	1	2	3	…
К2
1 2 3 … 5 … 11	161,45 18,51 10,13 … 6,61 …	199,50 19,0 9,55 …	215,72 19,16 9,28 …	…

К₁ – степень свободы чисоителя;

К₂ – степень свободв знаменателя.

Для линейной регрессии К₁ = 1.

ά – вероятность ошибки, т.е. можно ошибочно отвергнуть верную гипотезу с такой вероятностью.

К₂ = n-m-1 = 5

При 5 критерий Фишера табличный равен 6,61.

F_факт. < F_табл => Уравнение статистически не значимо с вероятностью 0,95. Уравнение не значимо, т.е. коэффициенты уравнения регрессии были получены случайным образом.

6)

Уравнение объясняет 15,2% дисперсии.

7) - t-статистика.

После вычисления t-статистики фактической, её нужно сравнить с табличным значением t. t-критерий (критерий Стьюдента) является двухсторонним, т.е. если мы получили t_a, t_b, t_r меньше 0, следовательно нужно взять

Фрагмент таблицы.

Число степеней свободы	ά
	0,10	0,05	0,01
1 2 … 5	6,3 2,9 … 2,01	12,7 4,3 … 2,57	63,6 9,9 … 4,03

ά – вероятность ошибки.

Мы гарантируем результат вероятностью равной (1- ά).

Число степеней свободы для линейной регрессии d · f = n – 2

t_bтабл. = 2,01 при ά = 0,1 => параметр b статистически не значим с вероятностью 0,9.

8) Вычисление прогноза

у_х ± t · m_ух

m_ух рассчитывается из данных, а t берется из таблицы при соответствующей степени свободы в зависимости от того, какой уровень значимости мы хотим получить при определенной степени свободы.