16.4. Системи масового обслуговування

з необмеженою чергою чекання

Подібні СМО використовуються в транспортних системах та інфраструктурах у випадках, коли є потреба в обслуговуванні транспортної одиниці, але немає вибору того чи іншого пункту обслуговування. Наприклад, у районі є тільки одна АЗС і поблизу немає іншої, тому автомобіль мусить чекати заправки, незважаючи на довжину черги чекання. Аналогічна ситуація з СТО, де автомобіль „терпляче” чекатиме ремонту, якщо поблизу немає іншої СТО. В окремих випадках автомобіль є закріпленим за певним пунктом навантаження або розвантаження, де він також мусить „терпляче” чекати завантаження або розвантаження.

Розглянемо спочатку одноканальну СМО з необмеженою чергою чекання. Граф станів такої СМО аналогічний зображеному на рис. 16.3 при умові m→∞. Отже, у загальному випадку кількість станів такої СМО не є обмеженою, що суперечить умові існування граничного (сталого) режиму. Але якщо кількість заявок, що надходить до СМО за одиницю часу (λ), не перевищує максимально можливу інтенсивність обслуговування, що визначається механізмом обслуговування ( ), в цьому випадку черга чекання обслуговування не може зростати нескінченно, тому кількість станів буде хоча й змінною, але зліченною, і граничний (сталий) режим такої СМО існуватиме. Математично умова існування граничного режиму запишеться у вигляді нерівності ρ < 1. Тільки при виконанні цієї умови можливе застосування рівнянь Колмогорова для розрахунків сталих значень імовірностей існуючих станів СМО.

Для визначення цих імовірностей приймемо m→∞ у відповідних формулах для СМО з відмовами та обмеженою чергою. Згідно з (16.37) та (16.38) при m→∞:

(16.74)

Оскільки обмежень на чергу немає і кожна заявка обов’язково дочекається обслуговування, то

(16.75)

Аналогічно для решти характеристик:

(16.76)

(16.77)

(16.78)

(16.79)

(16.80)

У випадку багатоканальної СМО з необмеженою чергою використовуємо той же самий підхід. Слід зауважити, що при n > 1 умовою існування граничного (сталого) режиму буде , тобто коефіцієнт навантаження одного каналу СМО не повинен перевищувати 1. Тільки при цій умові черга стабілізується у середньому на певному значенні. Відмітимо, що умова при заміні трансформується в умову , що має більш зрозуміле тлумачення обмеження: якщо інтенсивність вхідного потоку СМО є λ, а максимально можлива інтенсивність обслуговування одного каналу є , то сталий режим СМО існує, якщо 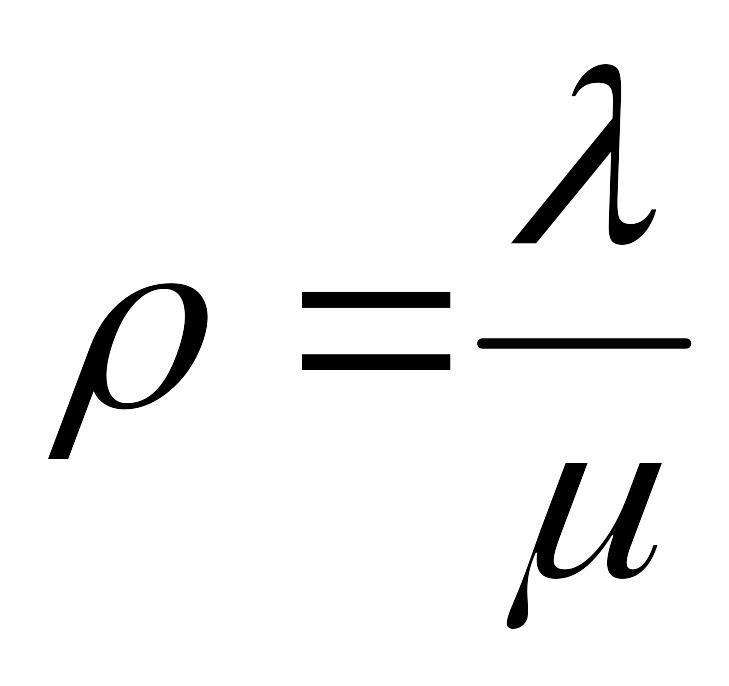менше кількості каналів обслуговування ( ). Тільки при забезпеченні цієї умови можливе застосування рівнянь Колмогорова для визначення імовірностей станів граничного режіму СМО.

Нехай граничний режим існує ( ). Тоді формули (16.53); (16.54); (16.56) для багатоканальної СМО з обмеженою чергою при m→∞ перетворюється у наступні формули:

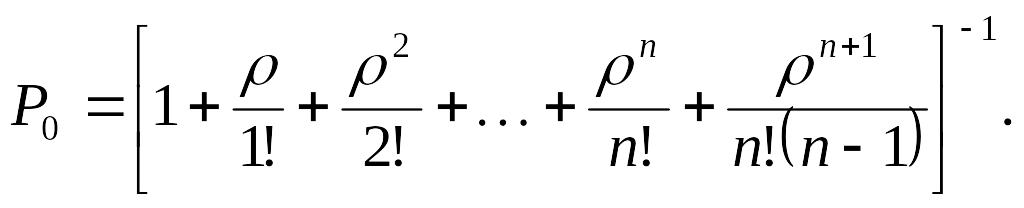(16.81)

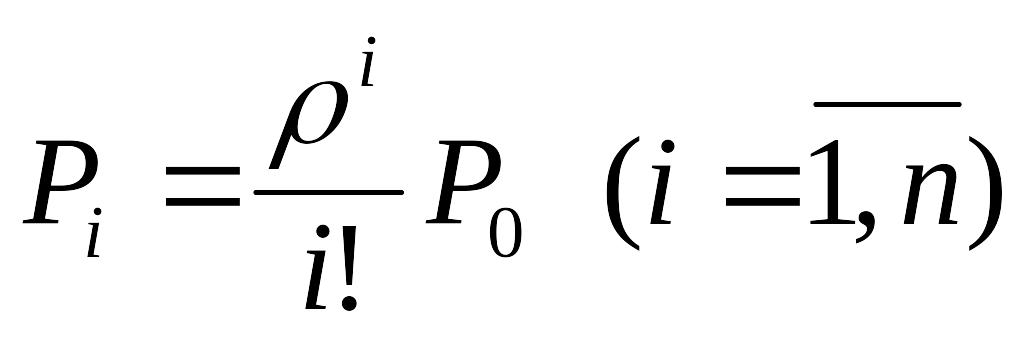– імовірності станів без черги (16.82)

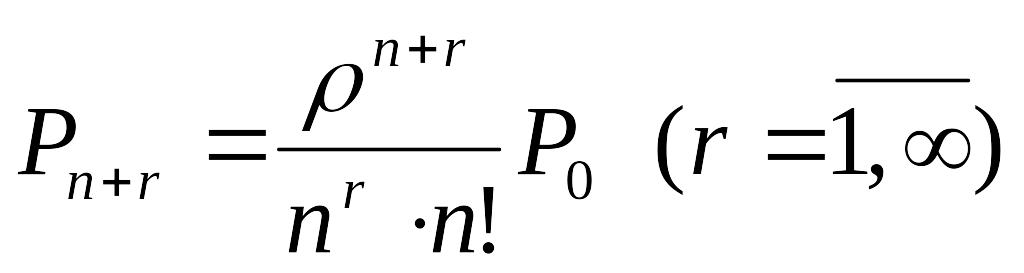– імовірності станів з чергою (16.83)

Як і в одноканальній СМО, для багатоканальної залишається справедливим наступне:

(16.84)

Решта параметрів визначиться з відповідних формул для багатоканальної СМО з обмеженою чергою при m→∞:

(16.85)

(16.86)

(16.87)

(16.88)

Для спрощення розрахунків і аналізу СМО з необмеженою чергою може бути використана вищезгадана програма PROG_2 при умові введення у вхідні дані досить значної величини m, при якій значення P_n+m стає такою малою величиною, що нею можна знехтувати (наприклад P_n+m < 0,001). У цьому випадку всі без виключення розрахункові характеристики відповідатимуть СМО з необмеженою чергою чекання.

СМО з необмеженою чергою чекання при наявності „нетерплячих” заявок. Розглянемо пуассонівську СМО з n > 1 та m→∞ з інтенсивністю вхідного потоку заявок та потоку обслуговувань при умові обмеження часу чекання певним значенням Т, яке є випадковою величиною, що підкоряється експоненційному закону розподілу з параметром (інтенсивність потоку втрат СМО за рахунок наявності „нетерплячих” заявок), де – середній інтервал обмеження часу чекання. Необхідно визначити граничні імовірності станів, абсолютну та відносну пропускні здатності А та q, а також ; ; ; .

Граф станів СМО відповідатиме загальному випадку (рис. 16.1) при умові , при m→∞. Визначимо, як завжди, та . Тоді

(16.89)

– черги немає (16.90)

– стани з чергою (16.91)

В формулу (16.89) входить нескінчена сума, що не є геометричною прогресією, але члени якої зменшуються значніше, ніж члени геометричної прогресії. Доведено, що похибка відхилення членів прогресії, починаючи з r, завжди менша за величину

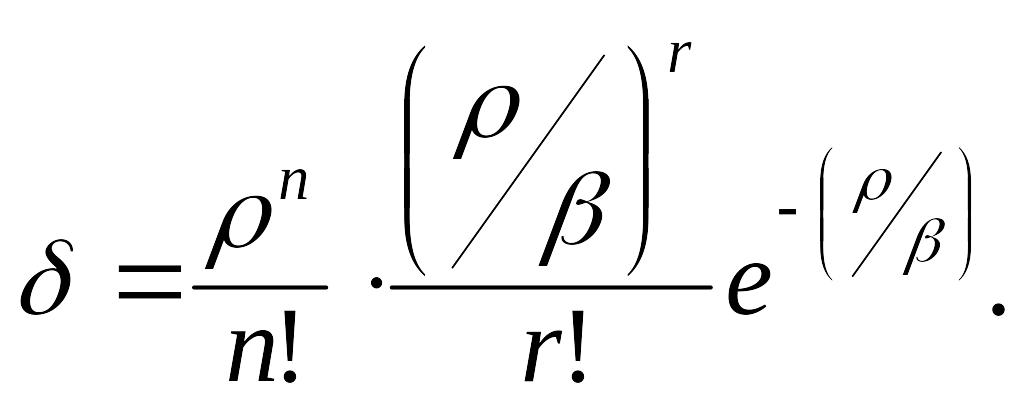(16.92)

Якщо , де r – середня кількість заявок у черзі, то інтенсивність потоку обслуговувань з урахуванням втрат СМО за рахунок присутності „нетерплячих” заявок:

(16.93)

Тоді

(16.94)

Таким чином, щоб визначити А та q, необхідно знати величину , яка визначалась раніше, як

(16.95)

Але в цій формулі значення m→∞, тобто кількість членів суми не визначена. Використовуємо залежність , де – середня кількість зайнятих каналів. Тоді, враховуючи (16.93), матимемо

(16.96)

звідки (16.97)

Значення можна підрахувати як

_(16.98)

Таким чином, спочатку визначаємо (формули 16.89 – 16.91) при умові, що задано величину r, яка забезпечує задану похибку δ згідно з (16.92). Потім визначається значення із застосуванням (16.98). Після цього визначаємо за формулою (16.97), після чого визначається, як завжди,

(16.99)

(16.100)

(16.101)

Важливою особливістю СМО з необмеженою чергою чекання при наявності „нетерплячих” заявок є те, що така СМО матиме завжди граничний режим роботи, навіть при , на відмову від подібної СМО при відсутності „нетерплячих” заявок (тобто при β = 0). Це пояснюється тим, що формула (16.89) завжди матиме кінцеве значення при будь-яких ρ та β. Практично це означає, що черга не може рости необмежено. Чим більша довжина черги, тим інтенсивніше заявки покидають чергу.

Багатоканальні СМО з різною продуктивністю каналів обслуговування. Подібні СМО мають місце в транспортних системах, де здійснюється навантаження автомобілів навантажувачами, що мають різну продуктивність.

В якості прикладу розглянемо СМО з двома каналами обслуговування. Нехай λ – інтенсивність вхідного потоку, та – інтенсивність кожного з каналів обслуговування, причому > .

Приймемо, що заявка, яка надходить до СМО, вибирає перший канал з імовірністю , тоді – імовірність вибору другого каналу обслуговування.

Введемо коефіцієнт нерівномірності обслуговування

Для цього випадку наведені формули для розрахунків імовірності станів кожного з каналів, які приводяться без доведення:

(16.102)

– імовірність вільного стану СМО;

(16.103)

– імовірність того, що перший канал зайнятий, а другий – вільний;

(16.104)

– імовірність того, що другий канал зайнятий, а перший – вільний;

(16.105)

– імовірність того, що обидва канали зайняті.

Середня кількість заявок в СМО

(16.106)

Аналіз такої СМО дозволяє зробити наступний висновок: якщо α близько до 1, а ψ достатньо далеко від 0, то значення близьке до , визначеної при α = 1, тобто для СМО з однаковою продуктивністю каналів.

Цей висновок значно спрощує дослідження СМО з кількістю каналів більше, ніж на 20 – 30%, то можна прийняти модель СМО, у котрій для кожного каналу приймається однаковою. Якщо різниця в продуктивності каналів >30%, можна прийняти модель СМО, в якій всі канали поділені на 2 класи з близькими інтенсивностями обслуговування й застосувати для них наведені вище розрахункові формули для визначення імовірностей та .

• Запитання для самоконтролю

1. В чому полягає загальний підхід до аналізу систем масового обслуговування ?

2. Що таке системи масового обслуговування з відмовами ?

3. Які є системи масового обслуговування з відмовами ?

4. Що таке обмеження черги чекання в системах масового обслуговування ?

5. Що таке необмеження черги чекання в системах масового обслуговування ?

278