Розділ 14 випадкові потоки подій

1. Пуассонівські потоки

2. Математичні моделі послідовностей часових інтервалів між подіями у потоці

3. Приклади моделей потоків подій в транспортних системах

Під потоками подій розуміють послідовність однорідних подій, що слідують одна за одною у деякі, в загальному випадку випадкові, моменти часу. Стосовно СМО під вхідним потоком подій розуміють потік вимог на обслуговування (наприклад, потік автомобілів, що прибувають на АЗС для заправки, де подією є прибуття одного будь-якого автомобіля, моментом здійснення події – момент його прибуття на АЗС, часовий інтервал між подіями – інтервал між моментами прибуття на АЗС цього та попереднього автомобіля), а також вихідний потік обслуговування (наприклад, потік заправлених автомобілів, що покидає АЗС). У деяких випадках розглядають також потік вимог, що не обслуговуються через дуже велику чергу очікування або відсутність вільних місць очікування. Цей потік часто зветься потоком втрат СМО (або потоком не обслужених вимог).

Як вже відмічалось, потік подій характеризується інтенсивністю λ, тобто частотою появи подій або середньою кількістю подій за одиницю часу. Потік подій є регулярним, якщо події відбуваються через рівні інтервали часу. Наприклад, пересічення „стоп-лінії” на регульованому перехресті впродовж роз’їзду черги автомобілів розглядають як регулярний. Регулярним також буде потік автомобілів з конвеєра збирального цеху, якщо швидкість конвеєра є незмінною.

На відміну від регулярного, випадковий потік характеризується нерівномірністю інтервалів часу слідування подій. Головною характеристикою випадкового потоку є імовірність попадання інтервалу часу між подіями в задане значення. При цьому розглядають, як правило, дві характеристики:

- імовірність появи поточного інтервалу t_i, меншого заданого значення τ, де τ та t_i, відраховуються від моменту здійснення (і – 1)-ї події. Ця характеристика має назву інтегральної функції розподілу імовірностей часових інтервалів слідування подій у потоці;

- щільність розподілу часових інтервалів слідування подій f(τ), що представляє собою похідну від f(τ), тобто:

і характеризує швидкість зміни f(τ) при зміні значення τ. Ця взаємозалежність свідчить, що при аналізі потоку подій досить знайти або f(τ), або f(τ).

В ТМО найбільш поширені саме випадкові процеси подій, при цьому він формалізується наступним чином.

Нехай – моменти надходження вимог на обслуговування в СМО (або моменти покидання СМО обслуженими вимогами). Величина – умовний момент розгляду початку потоку. Позначимо – інтервали часу між моментами звершення і-ї та (і – 1)-ї подій. Потік вважається заданим, якщо відомі значення . Додамо, що оскільки потоки випадкові, то необхідним для опису потоку є не стільки значення інтервалів, скільки їх імовірнісні характеристики f(τ) або Р(τ).

14.1. Пуассонівські потоки

Спочатку розглянемо потік подій, що задовольняє наступним умовам:

1) для будь-яких інтервалів часу, що не мають часового пересічення, імовірність появи певної кількості подій впродовж одного з них не залежить від кількості подій, що з’явились в іншому інтервалі. Ця властивість потоку в ТМО називається відсутністю післядії;

2) імовірність появи однієї події впродовж нескінченно малого інтервалу часу (t; t+Δt) є нескінченно мала величина порядку Δt;

3) імовірність появи двох або більше подій впродовж інтервалу (t; t+Δt) є нескінченно мала величина більш високого порядку, ніж Δt. Умови 2) та 3) означають практичну відсутність імовірності появи двох подій одночасно. Ця властивість потоку в ТМО називається ординарністю потоку;

4) імовірність появи m подій у певному інтервалі часу τ не залежить від моменту відрахування цього інтервалу, тобто при . Ця умова означає в ТМО, що потік подій є стаціонарним.

Позначимо – імовірність появи m подій в інтервалі часу . Тоді умови 2) та 3) запишуться у вигляді

(14.1)

(14.2)

де означає нескінченно малу величину більш високого порядку, порівняно з , такою, що ; – певна невід’ємна функція, що має бути визначена пізніше.

Поставимо задачу наступним чином: для потоку подій, що відповідають умовам 1), 2), 3), знайти ймовірність того, що в даному інтервалі з’явиться саме m подій (m = 0, 1, 2, ...).

Зафіксувавши на підставі умови 4) певне значення , позначимо імовірності . Для визначення відмітимо, що представляє собою імовірність пересічення двох подій: жодної події в інтервалі , а також жодної події в інтервалі . Згідно з умовою 1) ці обидві події незалежні, тобто

(14.3)

Тоді на підставі (14.1) та (14.2) матимемо

(14.4)

Використаємо (14.4) в (14.3) й отримаємо

(14.5)

звідки

(14.6)

Очевидно, що при права частина (2.6) прямує до , тобто існує границя й лівої частини (2.6). З цього походить, що є диференційованою функцією при будь-якому t та при :

(14.7)

Для знаходження слід взяти t = t₀ у рівнянні (14.5), тоді = l.

Для складання рівнянь для імовірностей P₁(t); P₂(t); ...; P_m(t) відмітимо, що m подій можуть заявлятися в інтервалі одним з наступних (m + 1) несумісних способів: всі m подій знаходяться в інтервалі і жодної – в інтервалі , (m – 1 ) – в інтервалі й одна подія в інтервалі , і т.д... Тому на підставі аксіоми про суму імовірностей та теореми про множення незалежних подій матимемо:

Потім, застосувавши (14.1), (14.2), (14.5), отримаємо:

звідки

(14.8)

(m= 1, 2, ...). При цьому початкові значення P_m(t₀) = 0, (m = l, 2, ...), оскільки було вже отримано .

Для визначення аналітичних залежностей P_m(t) введемо нову змінну:

(14.9)

тоді (14.7) та (14.8) приводяться до вигляду:

(14.10)

Враховуючи ; при t₀=0 і μ(0)=0, інтегрування рівнянь (14.10) при даних початкових значеннях приводить до наступного виразу імовірності появи m подій в потоці:

(14.11)

Таким чином, отримано аналітичну залежність для імовірності появи дискретної кількості подій (m = 0, 1, 2, ...) в функції змінної μ, що визначається за допомогою (14.9).

Цей розподіл імовірності в математиці носить назву розподілу Пуассона. Тому потоки подій, що відповідають вищеназваній умові 1) відсутності післядії та умовам ординарності потоку 2) та 3), носять назву пуассонівських потоків.

Змінна μ в рівнянні (14.11) має для потоку конкретний фізичний зміст: це кількість подій, що мають місце на інтервалі . Для спрощення виразу (14.11) можна прийняти до уваги середнє значення кількості подій в одиницю часу, що властиво для даного інтервалу , тобто

що в практиці називають середньою інтенсивністю подій на даному інтервалі.

Якщо то В цьому випадку

(14.12)

і відображає, крім властивостей ординарного потоку без післядії, також властивості стаціонарності потоку, тому що є певною константою, при m = const і = const. Такий потік подій має назву стаціонарного пуассонівського потоку подій (або найпростішого потоку). Саме цей потік є найбільш поширеною моделлю, що описує реальні потоки вимог на обслуговування та обслуговування в транспортних СМО.

Якщо реальні потоки вимог і обслуговувань є пуассонівськими, але не є найпростішими, то дуже часто використовується прийом заміни часового тренда через , де

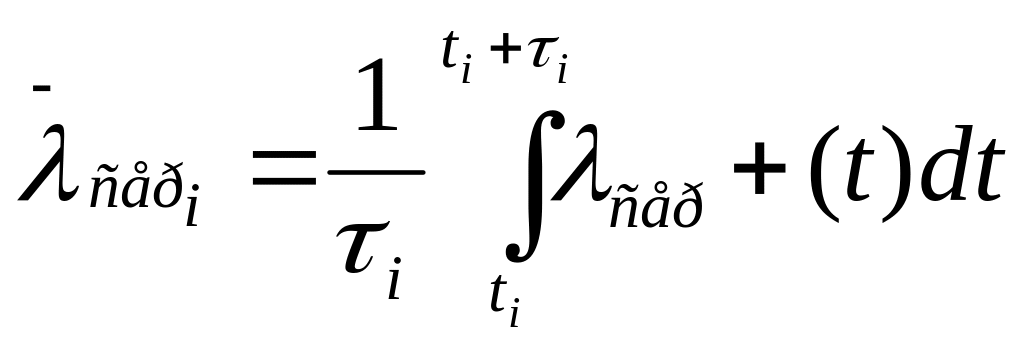– середня інтенсивність на і-му інтервалі розгляду. Тоді аналіз режимів СМО здійснюється із застосуванням моделі найпростішого потоку, що має , а отримані результати аналізу є притаманними лише інтервалу усереднення .

Завершуючи розглядання пуассонівського закону розподілу подій, відмітимо, що значення може трактуватися як імовірність появи саме m подій в інтервалі спостереження , яка визначається лише інтенсивністю надходження подій.

Для потоків, що відповідають розподілу Пуассона, варто визначити деякі узагальнені характеристики, дуже корисні для оцінки потоків подій.

1. Математичне сподівання

(14.13)

яке дозволяє оцінювати середню кількість вимог на обслуговування, що поступають або покидають СМО за час .

2. Дисперсія імовірних відхилень кількості вимог від за час :

(14.14)

або їх середнє квадратичне відхилення:

(14.15)

3. Мода

(14.16)

що характеризує максимальне значення імовірності прибуття саме m вимог за інтервал при інтенсивності .

4. Коефіцієнт варіації

(14.17)

Відмітимо, що коефіцієнт варіації V характеризує саме міру стабільності та розсіювання можливих варіацій m(t) відносно М(m). Для пуассонівських потоків V завжди дорівнює 1, але якщо не додержуватися перерахованих вище умов, що визначають розподіл Пуассона, значення V може коливатися в досить широких межах.