16.3. Системи масового обслуговування

з обмеженою чергою чекання

Цей тип СМО досить часто зустрічається в транспортних системах. Класичним прикладом подібної СМО є АЗС з одною або кількома заправними колонками (n ≥ 1 – кількість каналів обслуговування) при умові обмеженої кількості місць чекання заправки на майданчику АЗС (m ≥ 1 – кількість місць чекання у черзі). Якщо усі m місць чекання зайняті, автомобіль покидає АЗС необслугованим, створюючи тим самим потік відмов в СМО.

Розглянемо спочатку одноканальну СМО (n = 1) з обмеженням черги чекання (m – максимально можлива кількість заявок у черзі чекання).

Граф станів цієї системи представлений на рис. 16.3. при умові відсутності додаткових втрат заявок під час чекання ( ), а також у процесі обслуговування ( ).

На рис. 16.3, як завжди, S₀ – система вільна; S₁ – СМО зайнята, але черги ще немає; S₂ – СМО зайнята й є одна заявка у черзі; S_m+1 – m заявок у черзі чекання і більше немає місць чекання. Наступна заявка отримає відмову в обслуговуванні і покине СМО необслугованою.

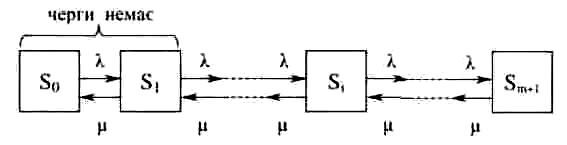
Рис. 16.3. Граф станів одноканальної СМО з обмеженою

чергою чекання

З урахуванням загальних формул для імовірності станів СМО при n = 1 та (див. формули (16.4); (16.5); (16.6)) матимемо:

1) імовірність вільного часу

(16.36)

Враховуючи, що вираз у дужках є геометричною прогресією з n = m+2 членів, з початковим членом а₁ = 1 та знаменником прогресії q = ρ, сума якої дорівнює

остаточно матимемо

(16.37)

2) імовірність решти станів СМО

(16.38)

Визначимо характеристики ефективності роботи СМО:

3) імовірність відмови в обслуговуванні

(16.39)

4) відносна пропускна здатність

(16.40)

5) абсолютна пропускна здатність (або інтенсивність обслуговування)

(16.41)

6) середня кількість заявок у черзі

(16.42)

Вираз в дужках є похідною по ρ від ряду , сума якого .

Візьмемо похідну по ρ від ∑:

(16.43)

Тоді (16.42) з урахуванням (16.43) запишеться у вигляді

(16.44)

З урахуванням (16.37) остаточно матимемо

(16.45)

7) середня кількість заявок, що є в процесі обслуговування

(16.46)

Прийнято , незважаючи на решту існуючих станів, тому що при будь-якому з станів СМО залишається завжди зайнятою, де обслуговується лише одна заявка;

8) кількість заявок, що пов'язана з СМО

(16.47)

9) середня тривалість чекання у черзі визначається як завжди

(16.48)

10) середній час перебування заявки в СМО

(16.49)

де – середній час обслуговування однієї заявки з урахуванням наявності вільного стану СМО.

Розглянуті вище формули для СМО є придатними лише при , тому що при формула (16.37) містить невизначеність типу . Тому розглянемо цей випадок окремо.

Згідно з загальновідомим правилом Лопіталя:

(16.50)

Тоді формули (16.37) та (16.38) матимуть при наступний вигляд:

(16.51)

Відповідно зміняться також формули (16.39 – 16.42), а також (16.46).

У випадку багатоканальної СМО з відмовами та обмеженнями черги граф станів матиме вигляд, зображений на рис. 16.1 при умові тобто без додаткових втрат заявок впродовж чекання та процесу обслуговування.

Застосовуючи загальні формули імовірності станів (16.4); (16.5); (16.6) при матимемо

(16.52)

– імовірності станів без черги (16.53)

– імовірності станів з чергою (16.54)

Дещо перетворюємо формулу для :

(16.55)

Вираз в круглих дужках є геометричною прогресією зі знаменником (ρ/n), сума якої

Тоді (16.55) перепишемо в остаточному вигляді

(16.56)

Таким чином, формули (16.56); (16.53); (16.54) повністю визначають імовірності усіх можливих станів розглянутої СМО.

Як і раніше, визначаємо характеристики ефективності роботи СМО:

1) імовірність відмов в обслуговуванні

(16.57)

2) відносна пропускна здатність

(16.58)

3) абсолютна пропускна здатність СМО (інтенсивність потоку обслуговувань)

(16.59)

4) середня кількість зайнятих каналів ( ).

Кожен зайнятий канал обслуговує у середньому μ заявок за одиницю часу, вся СМО обслуговує А заявок за одиницю часу, тому

(16.60)

5) середня кількість заявок у черзі чекання визначимо як математичне сподівання дискретної випадкової величини – числа заявок у черзі:

(16.61)

Приймемо – приведений коефіцієнт завантаження одного каналу багатоканальної СМО, що показує кількість заявок, що надходять за час обробки однієї заявки . Тоді

(16.62)

Вираз в дужках є похідна з ряду

,

що має суму

Взявши похідну d∑/dρ, як в формулі (16.43), отримаємо

(16.63)

що дозволяє переписати (16.61) у вигляді

(16.64)

який дозволяє розрахувати середню довжину черги чекання в СМО, що розглядається;

6) середня кількість заявок в СМО:

(16.65)

7) середній час чекання заявки в черзі ( ) визначається з наступних міркувань. Якщо заявка надійде, коли хоча б один канал є вільним, заявка не чекатиме. Якщо заявка надійде, коли усі n каналів зайняті, вона вимушена чекати у середньому (тому що інтенсивність потоку розвантаження n-канальної СМО дорівнює ). Якщо заявка надійде, коли усі n каналів зайняті та одна заявка вже є у черзі, вона вимушена чекати (по для кожної заявки у черзі). Якщо у черзі уже є r заявок, то . Якщо у черзі m заявок, то наступна вже не чекатиме, а покине СМО. З цих міркувань визначимо середній час чекання у черзі:

(16.66)

Порівняння (16.66) з (16.62) показує, що вони відрізняються тільки множником , тобто

(16.67)

Використовуючи формулу для , запишемо остаточно

(16.68)

8) середній час перебування заявки в СМО:

(16.69)

Як і в одноканальній СМО з відмовами та обмеженою чергою чекання при ρ = 1, в багатоканальній СМО існує аналогічна проблема аналізу при χ = 1, коли в формулі (16.56) матимемо невизначеність типу , а також в формулі (16.64), де матимемо 0 в знаменнику.

Щоб уникнути цих проблем, використовуємо, як і раніше, правило Лопіталя для виразу у круглих дужках формули (16.56) при :

(16.70)

Тоді формула (16.56) прийме вигляд

(16.71)

Імовірності інших станів СМО:

; (16.72)

На відміну від випадку СМО з , де змінюється з ростом r, при імовірність появи r заявок в черзі залишається незмінною. Подальші формули розрахунків (16.57 – 16.60) залишаються незмінними для СМО при . Формула ж (16.64) для розрахунків середньої кількості заявок у черзі ( ) матиме вигляд:

Остаточно матимемо

(16.73)

Решта формул залишається незмінними.