1.3. Задача вибору оптимального транспортного маршруту

Уявимо собі фірму, що займається перевезенням вантажів. Припустимо, що даній фірмі необхідно взяти в оренду на чотири роки визначену кількість транспортних засобів. Фірма може задовольнити свої потреби, узявши потрібну кількість транспортних засобів в оренду рівно на чотири роки (з початку першого року до початку п’ятого року). Відповідні витрати с₁₅ включають орендну плату, оплату за пробіг і експлуатаційні витрати, пов’язані з використанням транспортних засобів протягом чотирьох років. Можливий інший варіант: фірма може орендувати додаткову кількість транспортних засобів на термін з початку першого до початку третього року, а потім узяти під оренду інша кількість транспортних засобів на термін з початку третього до початку п'ятого року. В другому варіанті витрати, що включають ті ж компоненти, що й у першому випадку, дорівнюють с₁₃ + с₃₅. У більшості випадків с₁₅ с₁₃ + с₃₅. У пошуках стратегії, що забезпечує мінімальні витрати, можна, природно, розглянути і ряд інших варіантів. У цьому змісті мережна модель, зображена на рис. 1.4, є ілюстрацією задачі динамічного планування.

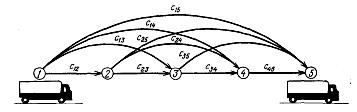
Рис. 1.4. Задача визначення найкоротшого маршруту

Питання, відповіді на які потрібно дати у зв’язку з розглядом мережі, представленої на рис. 1.4, пов’язані з перебуванням найкращого маршруту з вузла 1 у вузол 5. Ці питання можна поставити в двох різних, хоча і взаємозалежних варіантах:

1) Чому дорівнюють витрати для найдешевшого маршруту від вузла 1 до вузла 5?

2) Який маршрут від вузла 1 до вузла 5 сполучений з найменшими витратами?

Інтуїція підказує, що, відповідаючи на одне питання, ми одночасно одержуємо відповідь і на інше питання. Однак, переходячи до побудови моделі лінійної оптимізації, ми будемо шукати відповідь на кожне питання окремо, а потім проаналізуємо взаємозв’язок між сформульованими вище задачами. Почнемо з першого питання.

Витрати, пов’язані з використанням найбільш дешевого маршруту. Нехай:

y_i – витрати, пов’язані з використанням найбільш дешевого маршруту від вузла i до вузла 5, де i приймає одне зі значень i =1, 2 ,3 ,4.

Можна визначити у_i, підрахувавши витрати для прямого маршруту від вузла i до вузла j (j ~ i) і додавши до них витрати для оптимального маршруту від вузла j до вузла 5. Найменші з усіх вироблених при цьому витрат визначають значення у_i. Математично це можна сформулювати в такий спосіб:

(1.8)

Зокрема, для i = 1 маємо

(1.9)

Таким чином, витрати у випадку вибору найбільш дешевого маршруту від вузла 1 до вузла 5 можна визначити, якщо відомі витрати, зв'язані з використанням найбільш дешевих маршрутів від вузла 2 до вузла 5, від вузла 3 до вузла 5 і від вузла 4 до вузла 5. Отже, у цьому випадку задача зводиться до порівняння витрат, пов’язаних з використанням прямого маршруту від вузла 1 до вузла 5, з витратами при використанні маршруту від вузла 1 через кожний із проміжних маршрутів і вибору найкращого шляху від вузла 1 до вузла 5.

З позицій лінійного програмування задача полягає в тому, щоб

максимізувати 1у₁ (1.10)

при обмеженнях

(1.11)

Маршрут, пов’язаний з найменшими витратами. для рішення задачі вибору маршруту потрібно лише трохи узагальнити ті ідеї, що були основою при розгляді транспортної мережної моделі. Як і раніше, покладемо

х_ij = інтенсивність потоку від вузла i до вузла j (i = 1, 2, 3, 4), j > i.

Накладемо обмеження . Для знаходження найкращого маршруту (шляху) розглянемо одиничний потік, що виходить з вузла 1 і входить в інші вузли:

1х₁₂ + 1х₁₃ + 1х₁₄ + 1х₁₅ = 1. (1.12)

Будемо вважати, що всі потоки, що входять у вузли 2, 3 і 4, повинні випливати з них з наступним надходженням у вузол з більш високим порядковим номером:

–1х₁₂ + 1х₂₃ + 1х₂₄ + 1х₂₅ = 0 (вузол 2),

–1х₁₃ – 1х₂₃ + 1х₃₄ + 1х₃₅ = 0 (вузол 3), (1.13)

–1х₁₄ – 1х₂₄ – 1х₃₄ + 1х₄₅ = 0 (вузол 4).

Задача полягає в тому, щоб

мінімізувати (1.14)