Неоднозначность в нелинейных звеньях

Р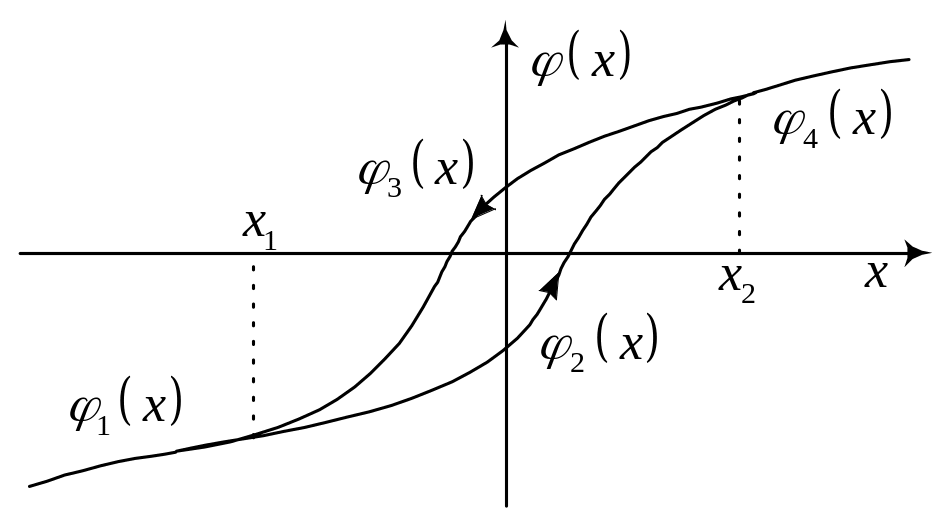 ассмотрим петлевую нелинейность, изображенную на рисунке. При и функция однозначна, но при значение функции зависит от знака производной аргумента. При увеличении значения аргумента ( ) , а при уменьшении ( ) – .

Т.о., учитывая зависимость нелинейной функции от производной аргумента, интегралы для определения коэффициентов линеаризации запишутся несколько сложнее:

; ; .

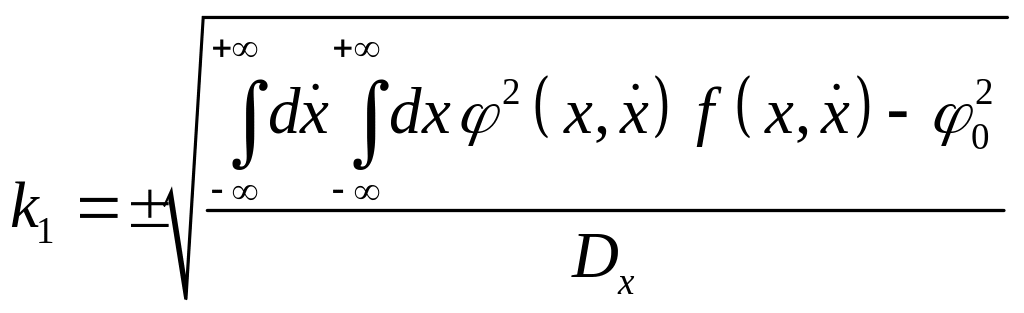На участках однозначной функциональной зависимости интегралы по в бесконечных пределах могут быть взяты и т.о. на этих участках мы получим исходные выражения для коэффициентов линеаризации с и в подынтегральных выражениях.

На участке интегралы по распадаются на два. Так, например, как в интеграле для определения :

.

В случае если функция является симметричной относительно плоскости (например, гауссовской с нулевым математическим ожиданием по аргументу ), то справедливым окажется следующее соотношение:

,

и, т.о., запись интеграла на интервале несколько упростится:

.

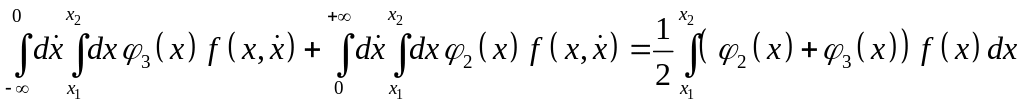Окончательно для рассмотренного примера получим:

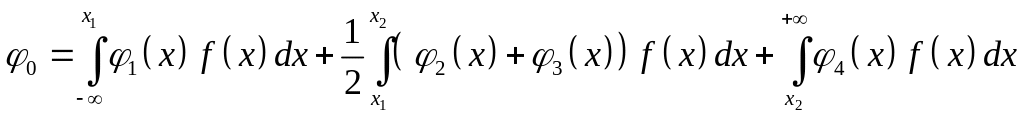
Вычисление двух оставшихся интегралов для , рассчитанных по первому и второму способам линеаризации, может быть выполнено по аналогии с рассмотренным выше примером.

Нелинейное звено, охваченное обратной связью

П усть входной случайный сигнал является гауссовским. В результате преобразования входного сигнала нелинейным звеном выходной сигнал уже не сможет оставаться гауссовским. А в случае если нелинейное звено, подлежащее статистической линеаризации, охвачено обратной связью, в формирование сигнала на входе в нелинейное звено вносит вклад не только входной гауссовский сигнал системы , но и выходной негауссовский сигнал .

В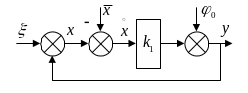 результате линеаризации звена возникнет ситуация, когда статистические характеристики сигнала на входе в нелинейное звено зависят в т.ч. и от результатов линеаризации.

Структурная схема системы, полученной в результате линеаризации, приобретет вид, изображенный на рисунке.

Д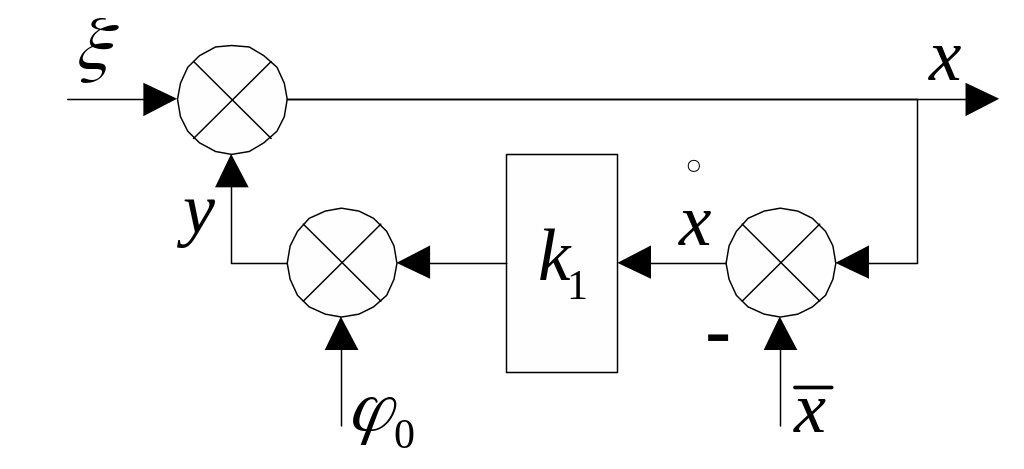 ля наглядности перерисуем схему так, чтобы выходным сигналом стал сигнал (вход в нелинейное звено).

Статистические характеристики выходного сигнала, необходимые для построения значений коэффициентов линеаризации, могут быть построены на основе использования следующих соотношений (см. раздел «Прохождение случайного сигнала через линейную систему»):

; ,

где:

– частотная характеристика системы с учетом результатов линеаризации; и – математическое ожидание и спектральная плотность входного сигнала системы .

В общем случае, когда на систему воздействует более одного случайного процесса , а система содержит более одного нелинейного звена с входными сигналами , необходимо построить множество передаточных функций от каждого входа к каждому выходу системы .

Окончательные соотношения для вычисления статистических характеристик сигналов имеют вид:

; .

Дисперсии компонент вектора могут быть вычислены при помощи интегрирования в бесконечных пределах по диагональных элементов матрицы :

.

Моделирование случайных процессов

Моделирование случайного процесса с заданными наперед математическим ожиданием и корреляционной функцией (или соответствующей ей спектральной плотностью ) выполняется на основе преобразования белого шума (с постоянной спектральной плотностью ) линейным динамическим звеном, именуемым формирующим фильтром, с передаточной функцией , подлежащей определению из соотношения:

.