Первый способ

В соответствии с первым способом статистической линеаризации коэффициент выбирается исходя из условия равенства дисперсий исходного и эквивалентного сигналов. Т.о. для вычисления получим следующее соотношение:

,

где – дисперсия входного случайного воздействия.

Знак в выражении для определяется характером зависимости в окрестности значения аргумента . Если возрастает, то , а если убывает, то .

Второй способ

Значение по второму способу выбирается из условия минимизации средней квадратической ошибки линеаризации:

, где .

Окончательное соотношение для вычисления коэффициента по второму способу имеет вид:

.

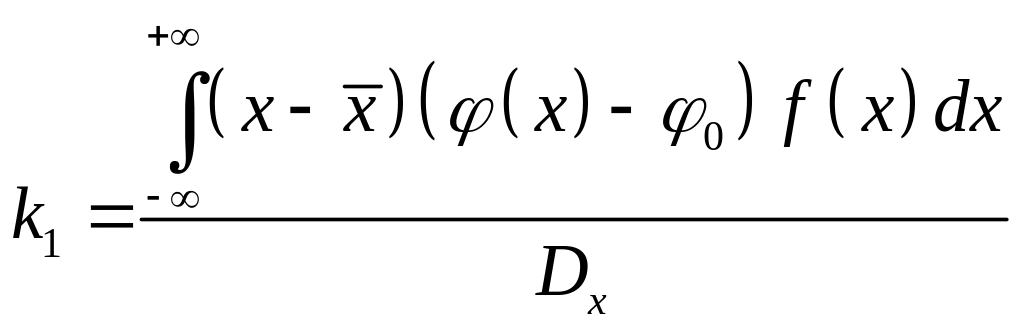В заключение заметим, что ни один их двух, рассмотренных выше, способов линеаризации не обеспечивает равенства корреляционных функций выходных сигналов нелинейного и эквивалентного звеньев. Расчеты показывают, что для корреляционной функции нелинейного сигнала первый способ выбора дает оценку сверху, а второй способ – оценку снизу, т.е. ошибки в определении корреляционной функции нелинейного выходного сигнала имеют разные знаки. Проф. И.Е. Казаков, автор, изложенного здесь метода, рекомендует выбирать в качестве результирующего коэффициента линеаризации полусумму коэффициентов , полученных по первому и второму способам.

Вычисление коэффициентов линеаризации

С учетом того обстоятельства, что большинство нелинейных элементов в заданиях представляют собой кусочно-линейные функции входного сигнала, становится очевидно, что подынтегральные выражения в интегралах

при вычислении значений коэффициентов и или содержат произведение степенного полинома входного сигнала и плотности его распределения .

Неизвестная плотность распределения может быть с высокой точностью аппроксимирована гауссовской. Обоснование этого решения состоит в том, что инерциальная динамическая система в любом из заданий обладает эффектом нормализации закона распределения входного случайного воздействия, фактически, суммируя значения сигналов с разными запаздываниями (по причине инерциальности системы).

Построим соотношения для вычисления значений интегралов вида:

,

где: и – нижний и верхний пределы интегрирования; 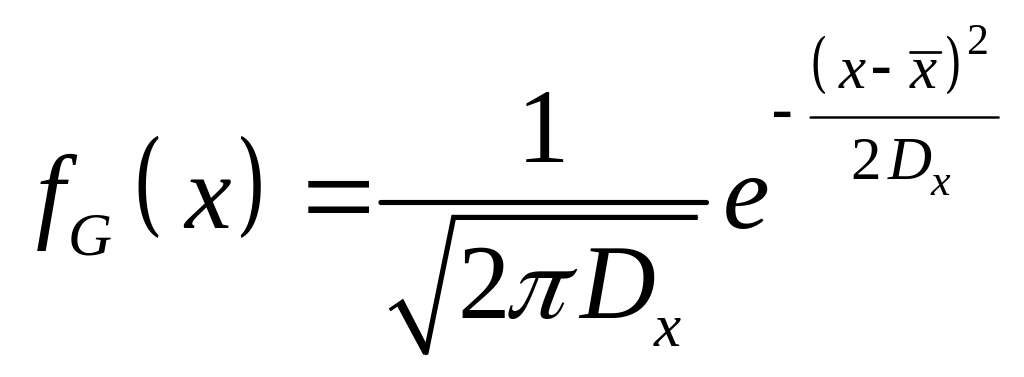– Гауссовская плотность распределения случайной величины ;

– целое неотрицательное число.

При построении окончательных выражений для интеграла используем следующее соотношение:

,

где 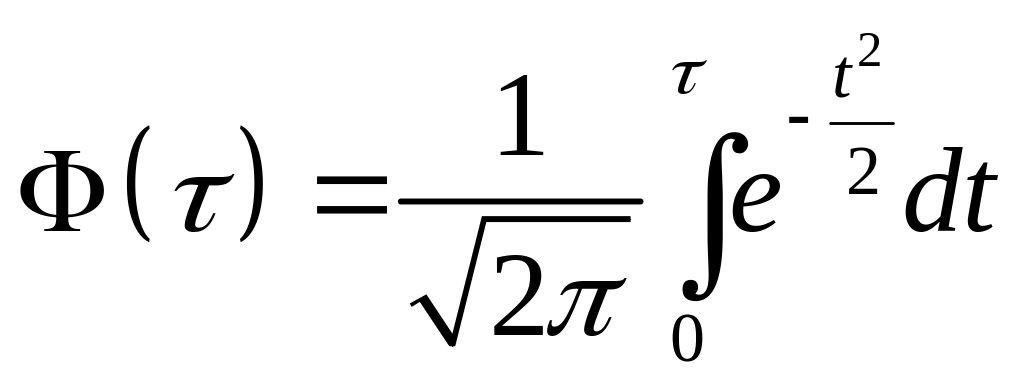– интеграл вероятностей, обладающий следующими свойствами:

;

Т.о., с учетом введенной в рассмотрение функции, получим:

;

Дифференцируя гауссовскую плотность по , получим:

.

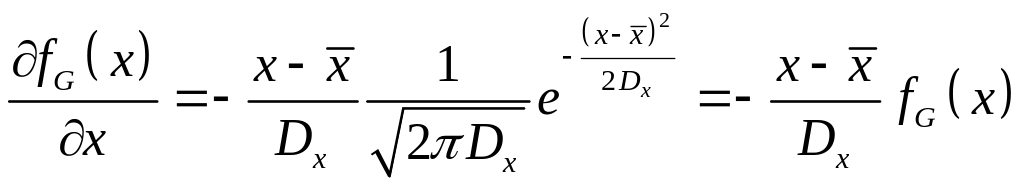С использованием результатов дифференцирования:

.

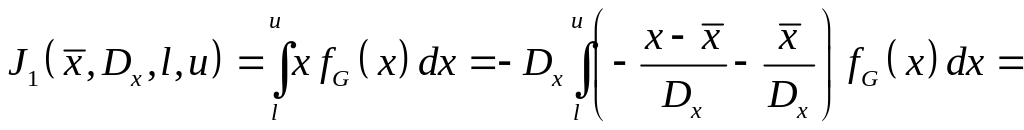
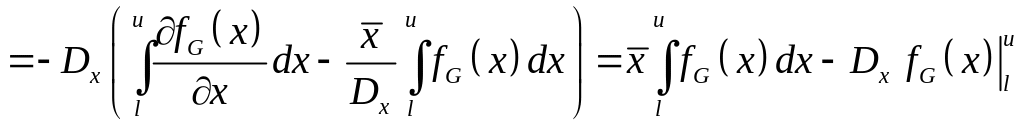Используя введенные ранее обозначения, получим окончательный результат интегрирования:

.

Интегрируя по частям выражение для с учетом приведенных выше соотношений получим:

.

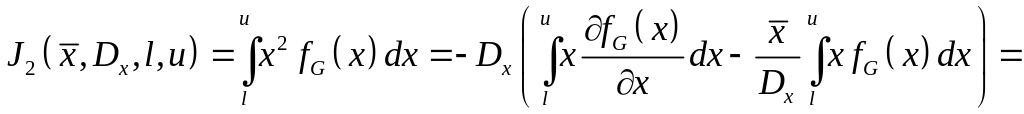
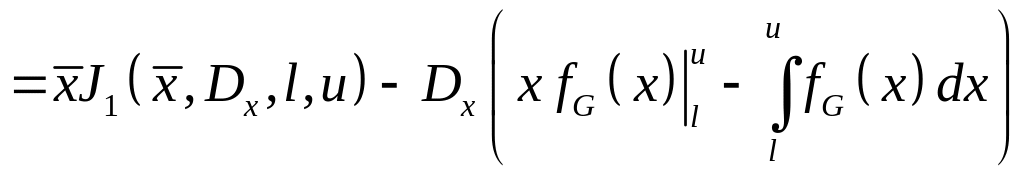Окончательно имеем:

.

При необходимости процесс вычисления интегралов для более высоких степеней в подынтегральном выражении может быть продолжен интегрированием по частям.

Приведенные выше интегралы позволяют существенно упростить многократный процесс построения параметров линеаризации с использованием вычислительной техники.

Р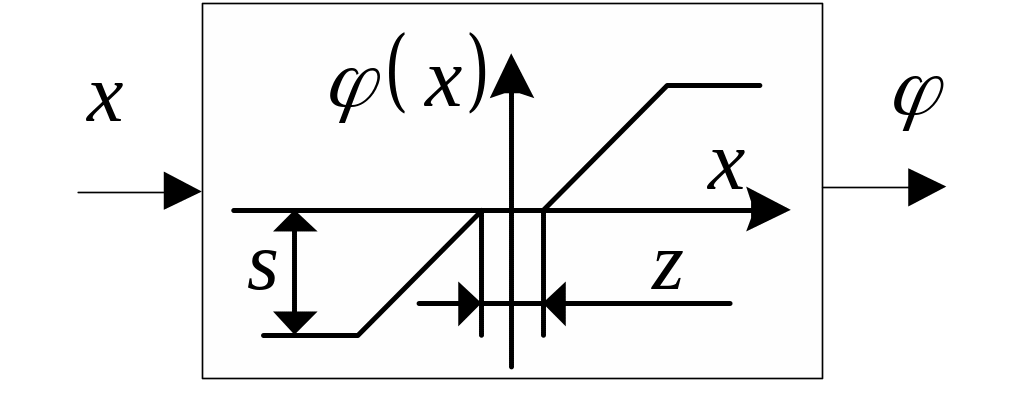 ассмотрим, например, нелинейное звено, обладающее симметричной относительно начала координат функциональной зависимостью с насыщением с зоной нечувствительности . Наклонные участки составляют с осью абсцисс угол 45. Входной гауссовский случайный процесс обладает математическим ожиданием и дисперсией .

Т.о. – кусочно-линейная функция:

Вычислим значения параметров линеаризации в соответствии с приведенными соотношениями:

.

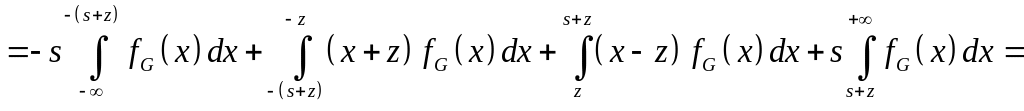
Интеграл в числителе выражения для коэффициента , рассчитанного по первому способу линеаризации, может быть несколько упрощен:

.

Т.о.

,

где:

.

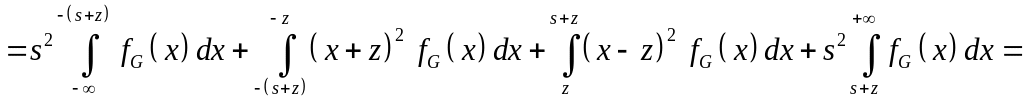
Интеграл в числителе выражения для коэффициента , рассчитанного по второму способу линеаризации, также как и в предыдущем случае может быть несколько упрощен:

.

т.о. значение коэффициента линеаризации , рассчитанного по второму способу, примет вид:

,

где

.

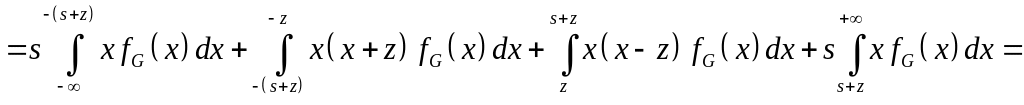
В случае если , приведенные соотношения несколько упростятся.