Гауссовские случайные величины
В настоящем подразделе описаны несколько
способов генерации гауссовских случайных
величин
с заданными математическим ожиданием
и дисперсией
на основе использования стандартных
равномерно распределенных случайных
величин
.
Первый способ основывается на использовании свойства суммы случайных величин, связанного со стремлением закона ее распределения к гауссовскому:
.
Хорошее совпадение закона распределения
случайной величины
с гауссовским получается при
.
Однако, приведенное соотношение
существенно упрощается при
:
.
Основной недостаток данного способа
генерации гауссовской случайной величины
связан с тем, что для этой цели используется
(12 или более) равномерно распределенных
случайных величин. Т.о. производительность
метода составляет
.
Второй способ связан с использованием … и является наиболее предпочтительным с точки зрения простоты реализации:
,
где
– случайная величина, распределенная
по закону Рэлея:
.
Для генерации случайной величины
используется только две равномерно
распределенных случайных величины.
Производительность метода т.о. составляет
.
Наиболее высокой производительностью обладает третий способ генерации гауссовских случайных величин:
;
,
где нормирующий множитель
определяется следующим соотношением:
.
При этом
– сумма квадратов двух тех же самых
равномерно распределенных случайных
величин
и
:
,
п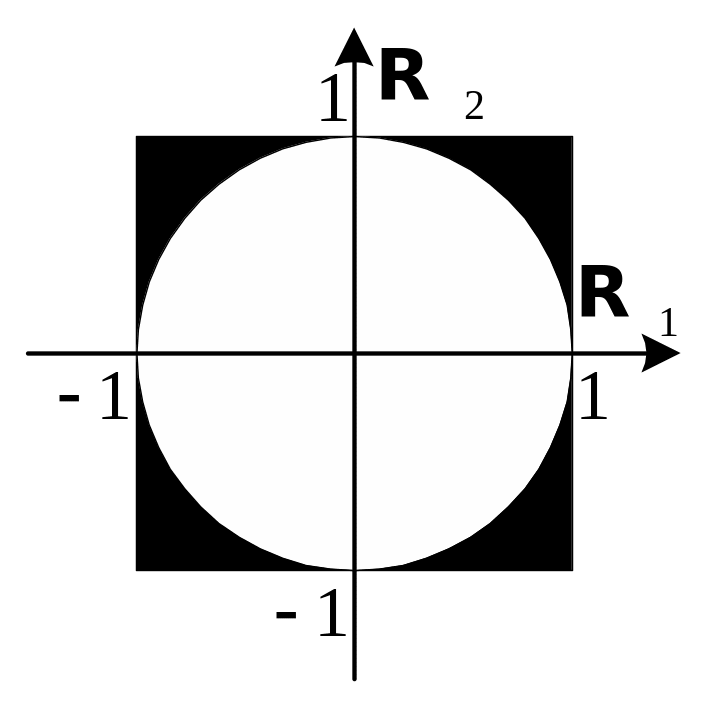
ри
этом гауссовские случайные величины
могут быть построены только в случае,
если
.
Именно на этой проверке приведенный
алгоритм теряет часть своей
производительности. Все возможные
сочетания случайных величин
и
представляют собой квадрат со стороной
2, а сочетания тех же вичин, удовлетворяющих
условию проверки – круг с радиусом 1.
Т.о. производительность алгоритма равна
вероятности попадания случайного
вектора
в упомянутый выше круг, что составляет
.
В случае, если Вы располагаете датчиком
случайных гауссовских стандартных
чисел
в составе какой-либо библиотеки, то
моделирование случайных гауссовских
величин с произвольными значениями
параметров может быть выполнено на
основе использования значений
следующим образом:
.
Случайные векторы
Проблема, решение которой описано в настоящем подразделе, состоит в моделировании вектора коррелированных между собой гауссовских случайных величин.
Пусть случайный вектор
,
подлежащий моделированию, формируется
на основе преобразования вектора
стандартных некоррелированных случайных
величин
соответствующей размерности следующим
образом:
,
где
– вектор математического ожидания
;
– матрица коэффициентов, подлежащих
определению.
Как известно, ковариационная матрица вектора , отвечающего приведенной выше зависимости, может быть определена на основе следующего соотношения:
.
Пусть матрица имеет вид:
.
Тогда, приравнивая левую и правую части
уравнения поэлементно, для каждого
из, например, нижнего треугольника,
получим совокупность
уравнений вида:
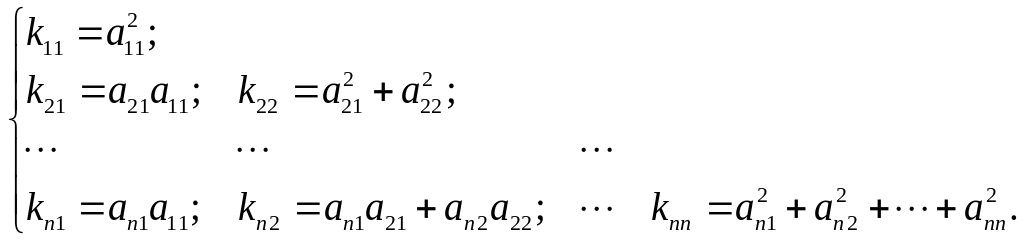
Разрешая полученные уравнения относительно элементов матрицы , получим окончательные соотношения:
Т.о. для получения вектора коррелированных случайных величин необходимо вычислить элементы матрицы в соответствии с приведенными выше формулами и сгенерировать реализации элементов вектора гауссовских случайных некоррелированных величин , после чего воспользоваться исходным соотношением подраздела.