2.4. Теорія теплоємності кристалічної ґратки

Правильність уявлень про рух атомів кристалічної ґратки можна перевірити порівнюючи висновки теорії, побудованої на їх основі, з результатами експериментальних вимірювань теплоємності, теплопровідності та теплового розширення ґратки. Історично процес побудови теорій такого типу та їх порівняння з експериментом супроводжувався подальшим розвитком уявлень про закономірності теплового руху атомів у кристалах і введенням нових понять, необхідних для розуміння інших властивостей твердих тіл. Тому розглянемо коротко їх основні риси і висновки.

Класична теорія теплоємності. Найпростішою, моделлю кристала, можна вважати сукупність N атомів, що коливаються відносно положень рівноваги у трьох ортогональних напрямках незалежно один від одного. При цьому кожний з них володіє трьома ступенями вільності, так що кристал – система N атомів, володіє 3N ступенями вільності.

Згідно висновків класичної термодинаміки на кожний ступінь вільності руху системи, яка знаходиться у стані термодинамічної рівноваги, припадає середня кінетична енергія

(2.16)

де k_B – стала Больцмана, T – термодинамічна температура. Згідно класичної механіки, середня кінетична енергія руху частинки, що здійснює коливання під дією пружних сил, дорівнює її середній потенціальній енергії. Отже, на кожний ступінь вільності атома у кристалі припадає повна енергія k_ВT, так що повна енергія коливань усього кристала

. (2.17)

Тоді теплоємність кристалу

(2.18)

визначається тільки кількістю атомів і не залежить від їх сорту, а тому теплоємності різних твердих тіл, що містять однакову кількість атомів, мають бути однаковими.

Цей висновок класичної теорії теплоємності твердого тіла підтверджений експериментально Дюлонгом і Пті: молярна теплоємність усіх хімічно простих кристалічних твердих тіл дорівнює 3R (R = k_ВN_A – універсальна газова стала). У випадку складних речовин кількість атомів кристалічної ґратки повинна бути рівною числу Авогадро N_A.

Пізнішими дослідами в області низьких температур було встановлено, що сформульований вище закон Дюлонга - Пті не виконується при низьких температурах. З пониженням температури нижче деякого значення T_D, теплоємність кристалів зменшується пропорційно до T³. При цьому коефіцієнт пропорційності і величина T_D залежать від сорту кристала.

Квантова теорія теплоємності. Пояснити зменшення теплоємності твердих тіл до нуля при зниженні їх температури стало можливим тільки на основі квантової теорії, згідно якої, енергія коливного руху квантується, так що кожному нормальному коливанню з частотою ω відповідає дискретний набір дозволених значень енергії

, (2.19)

(n = 0, 1, 2, ... – коливне квантове число).

З (2.19) випливає, що енергія нормального коливання може змінюватись порціями (квантами), кратними величині ħω, причому найменше її значення становить величину ħω/2. Другий з цих висновків може бути сформульований ще й так: у природі не існує кристалів атоми яких не коливаються. Коливання з мінімальною енергією ħω/2 називаються нульовими. Відібрати енергію нульових коливань від кристала можливо тільки зруйнувавши його ґратку (тобто кристал). Отже, енергія нульових коливань для даного кристалу є величиною сталою, її неможливо передати іншому тілу. Це означає, що нульові коливання не приймають участь у процесах теплопередачі. Тому при вивченні теплових процесів, зокрема при визначенні теплоємності кристалу, замість (2.19) зручніше використовувати співвідношення

. (2.20)

Виходячи з (2.20) А. Ейнштейн зробив висновок, що кристал, як коливна система, збуджена до n-го рівня (тобто володіє енергією nħω), може вважатись множиною n невзаємодіючих частинок з енергією ħω кожна. Такі уявні (віртуальні) частинки – носії енергії теплових коливань у кристалі називають фононами. Отже, складний рух усієї сукупності атомів кристалу – поширення хвиль усіх можливих напрямків, частот, довжин хвиль і поляризацій, можна трактувати як рух всередині нього фононів різного типу (акустичні, оптичні), поляризації (поздовжні, поперечні) і частоти.

Ейнштейн показав також, що в стані термодинамічної рівноваги середня енергія нормального коливання з частотою ω складає величину

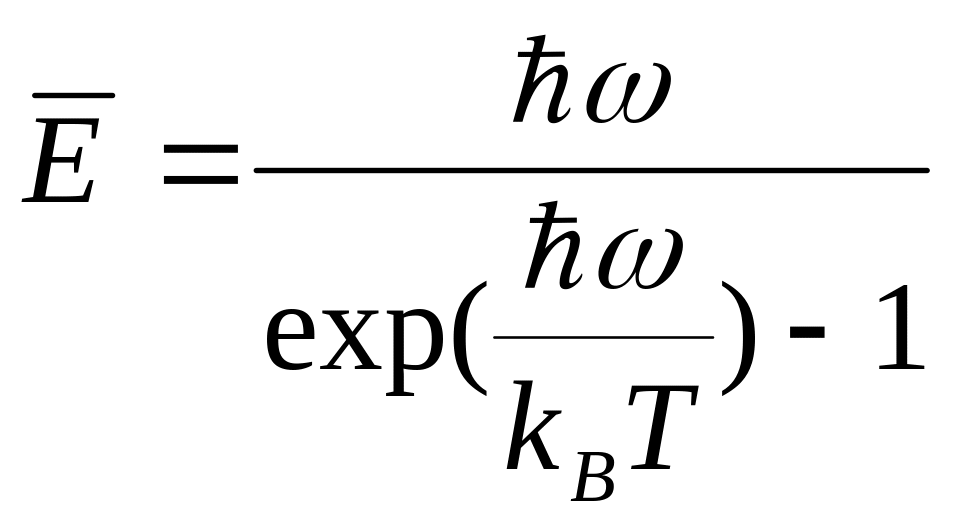, (2.21)

тобто моді коливань з частотою ω відповідає в середньому

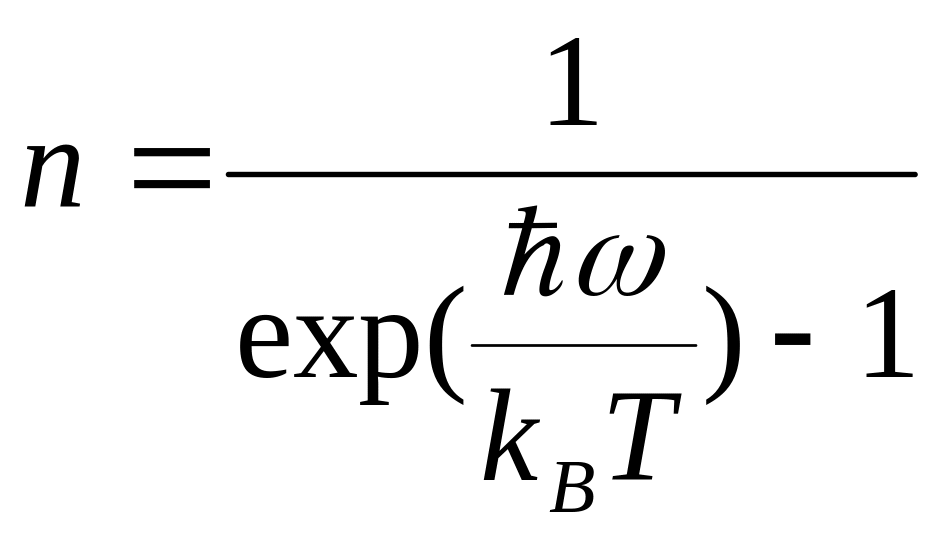(2.22)

фононів з енергією ħω кожний. Фонони з’являються у кристалі при його нагріванні; їх кількість стрімко зростає при збільшенні температури, а при охолодженні – зникають.

Припускаючи, для простоти, що усі 3N мод у кристалі характеризуються однаковою частотою коливань ω, енергію ґратки можна подати у вигляді

, (2.23)

а її теплоємність –

. (2.24)

Проаналізуємо (2.24) у двох крайніх випадках – за умови високих (таких, що k_BT >> ħω) та низьких (тобто k_BT << ħω) температур.

При високих температурах виконується умова ħω/k_BT << 1, а тому

. (2.25)

Підставляючи (2.25) у (2.24) і нехтуючи величинами вищих порядків малості, отримуємо закон Дюлонга – Пті.

У області низьких температур , а тому

, ,

так що .

Різниця результатів, отриманих для області високих і низьких температур полягає у різній кількості фононів. При низьких температурах їх концентрація мала і суттєво залежить від температури. Тому малою і суттєво залежною від температури виявляється і теплоємність ґратки. При високих –концентрація фононів і, відповідно, енергія теплового руху практично за лінійним законом зростають при збільшенні температури, а тому теплоємність від неї не залежить.

Отже теорія Ейнштейна, яка ґрунтується на уявленнях квантової механіки про квантованість енергії теплового руху, носієм якої є фонон, пояснила експериментально спостережувані факти – виконання закону Дюлонга – Пті у області високих температур і зменшення до нуля теплоємності ґратки із зменшенням температури. Це означає справедливість уявлень про тепловий рух атомів у кристалах.

Проте, висновки теорія Ейнштейна для області низьких температур пояснюють результати експериментальних досліджень тільки якісно. Кількісного результату – C ~ T³, вона не досягла. Причина цього полягає не у хибності уявлень про тепловий рух атомів, а суттєве спрощення задачі – розгляд тільки одного типу фононів.

Подальше вдосконалення квантової теорії теплоємності кристалічної ґратки було здійснене Дебаєм, який температурну залежність теплоємності кристалічної ґратки з урахуванням частотного розподілу нормальних коливань. Для цього потрібно знати, скільки різних мод відповідає тому чи іншому значенню частоти коливань. Оскільки дозволені значення на шкалі частот розташовані надзвичайно щільно, то наближено з частотою можна поводитись як з неперервно змінною величиною. Це дозволяє використати поняття визначеної для неперервних величин щільності розподілу мод по частотах – залежної від ω функції g(ω), такої, що величина g(ω)dω визначає кількість мод, яка припадає на частотний інтервал (ω, ω + dω).

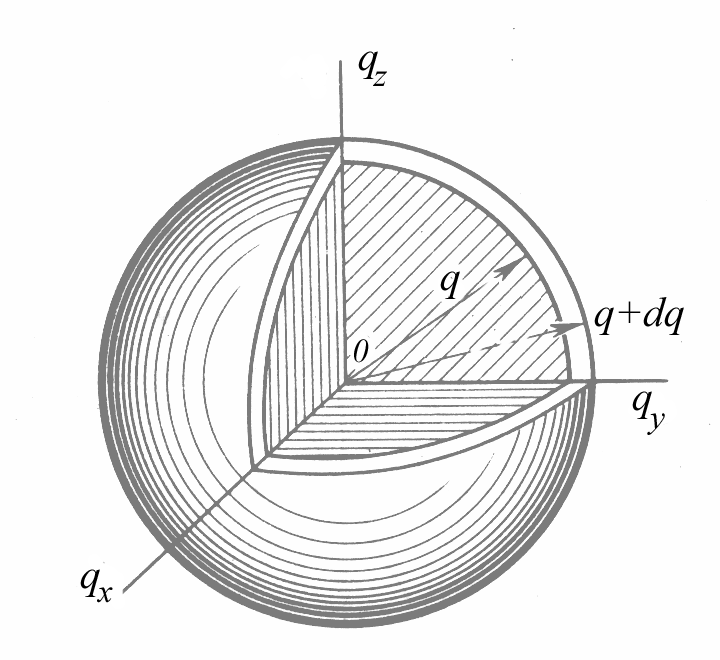
Задача обчислення функції g(ω) у тривимірному кристалі в загальному випадку є дуже складною. Тому, зазвичай, її істотно спрощують, вводячи наступні припущення. По-перше, вважають, що частота коливань ω залежить тільки від модуля хвильового вектора . Тоді довільному інтервалу частот (ω, ω + dω) буде відповідати множина дозволених значень хвильного вектора (q, q + dq) у вигляді точок, що містяться всередині сферичного шару у тривимірному -просторі (рис. 2.7). Кількість різних значень хвильового вектора, які попадають у цей шар одержимо, поділивши об’єм шару 4πq²dq на об’єм 8π³/Ω, що припадає на одне значення :

Рис. 2.7. Шар товщиною dq у просторі хвильових векторів (не-заштрихована область)

. (2.26)

Далі, для знаходження g(ω), необхідно перейти від змінної q до ω використовуючи дисперсійне співвідношення (залежність ω від q). Скільки явний вигляд його у реальному кристалі невідомий, то використовується друге припущення: залежність ω від q вважається лінійною (як це має місце у випадку довгих хвиль акустичних коливань атомів одновимірної ґратки), тобто покладається для поздовжніх, та – для обох поперечних хвиль.

Тоді відповідна заміна змінних і врахування (2.26) дає змогу знайти щільність розподілу мод за частотами коливань у вигляді

(2.27 а)

для поздовжних коливань і

– (2.27 б)

для обох поперечних поляризацій, так що повна щільність розподілу має вигляд

. (2.28)

Розглянуті міркування справедливі до тих пір, поки сферичні поверхні у оберненому просторі не почнуть виходити за межі першої зони Бріллюена. Для врахування цього факту Дебай запропонував третє спрощення – замість істинної зони Бріллюена – многогранника складної форми, – розглядати сферу того самого об’єму і, відповідно, з тою ж самою кількістю мод 3N). Радіус цієї сфери q_D знаходиться з рівності

, (2.29)

звідки . Очевидно, величина вектора визначає максимальні частоти поздовжніх та поперечних коливань ω_D = υq_D.

У випадку ґраток кубічної сингонії швидкість поширення хвиль однакова для усіх напрямків ( ), а тому

(0 ≤ ω ≤ ω_D),

де

– (2.29)

максимально можлива частота коливань атомів ґратки (Дебаївська частота). Тоді для кубічних ґраток щільність розподілу мод за частотами коливань набуває вигляду

(0 ≤ ω ≤ ω_D). (2.30)

Графік функції (2.30) приведений на рис. 2.8 (пунктир) разом з графіком щільності мод для кубічної зони Бріллюена, розрахованої у рамках більш точної моделі (суцільна крива). Відзначимо, що хоча справжній хід залежності g(ω) відрізняється від того, що одержано у наближенні Дебая, функція g(ω) у обох випадках досягає максимуму поблизу ω_D. Тому, у разі необхідності оцінки значення частоти коливань атомів у кристалі, її беруть близькою до ω_D.

Рис. 2.8. Щільність розподілу мод за частотами нормальних коливань

Знайдений вигляд частотного розподілу мод дозволяє встановити теплоємність ґратки. Помноживши кількість мод g(ω)dω, що припадає на інтервал частот (ω, ω + dω), на середню енергію нормальних коливань , одержимо сумарну енергію коливань, частоти яких належать вказаному інтервалу:

.

Енергія теплових коливань кристалічної ґратки, очевидно, буде сумою енергій усіх можливих нормальних коливань; знайдемо її шляхом інтегруванням :

. (2.31)

Для знаходження температурної залежності теплоємності необхідно продиференціювати (2.31) за змінною Т. При цьому у області високих температур знову одержується закон Дюлонга - Пті, а для низьких, де k_BT << ħω_D і

, –

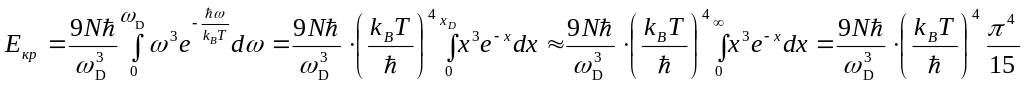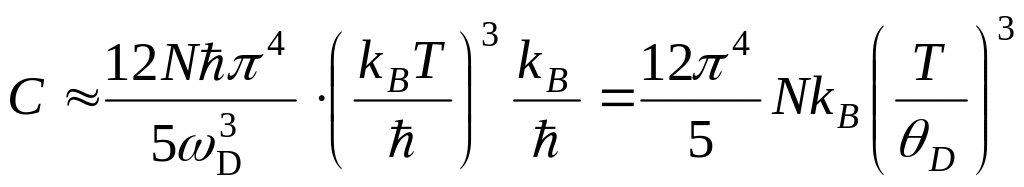(2.32)

(тут – нова змінна інтегрування, а – так звана температура Дебая). Отже, при T << θ_D теплоємність ґратки залежить від температури, змінюючись пропорційно до Т³. Коефіцієнт пропорційності залежить від властивостей кристала через параметр θ_D (рис. 2.9).

Рис. 2.9. Температурна залежність теплоємності кристалу

При розгляді теорії теплоємності кристалічної ґратки використовувалося гармонійне наближення, згідно якого сила, що виникає при зміщенні атома з положення рівноваги, пропорційна величині зміщення u. Побудована у такому наближенні теорія теплопровідності узгоджується з результатами вимірювань у кристалах Au, Al, Cu, NaCl, алмазу та ряду інших матеріалів не тільки якісно, що свідчить про справедливість уявлень про рух атомів у кристалах. Проте, в цьому наближенні неможливо пояснити ряд інших явищ, пов’язаних з тепловими коливаннями, наприклад, теплове розширення та теплопровідність твердого тіла.