2.2. Коливання атомів складної одновимірної ґратки

Розглянемо тепер ланцюжок, що складається з атомів двох сортів (рис. 2.4), наприклад різної маси – m і М (m < M). Записавши рівняння руху для кожного сорту атомів, отримаємо систему

Рис. 2.4. Модель складної одновимірної ґратки

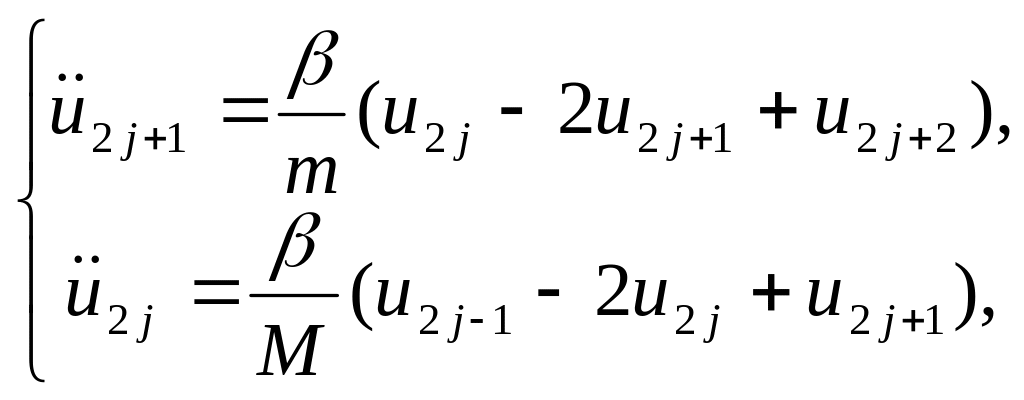(2.8)

розв’язок якої також будемо шукати у вигляді плоскої хвилі. Проте, внаслідок різних мас сусідніх атомів, амплітуди і фази у цих точках будуть різними. Тому покладемо

, , (2.9)

підставимо їх у (2.8) і отримаємо лінійну однорідну систему алгебраїчних рівнянь

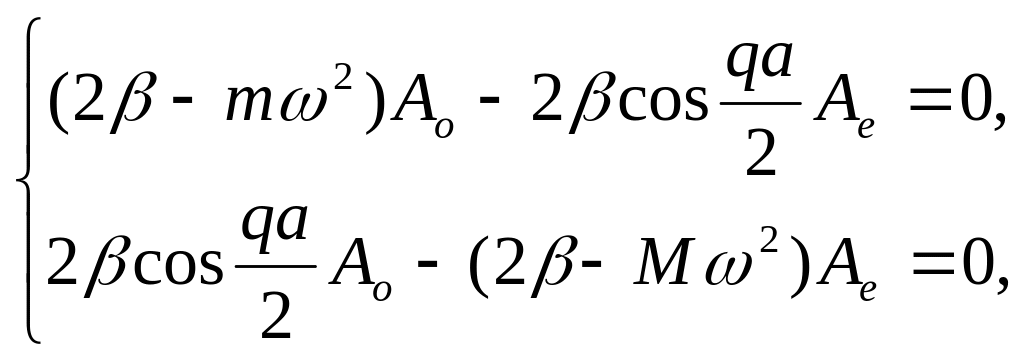(2.10)

яка має ненульові розв’язки за умови

, (2.11)

де – приведена маса атомів.

У випадку довгих хвиль (qa << 1) виконується умова , так що (2.11) набуває вигляду

(2.12)

звідки знаходимо, що на відміну від випадку простої одновимірної ґратки тут частота коливань стає двозначною періодичною (з періодом 2π/a) функцією хвильового вектора – кожному значенню q відповідає два значення частоти:

(2.13)

та

. (2.14)

Легко бачити, що хвилі, частота яких визначається дисперсійним співвідношенням (2.13), подібні до хвиль, які відповідають тепловому руху атомів простої одновимірної ґратки. Дійсно, на інтервалі-періоді функції (2.13) частота зростає від значення ω(0) = 0 у центрі зони Бріллюена до найбільшого – , – на її краях, а. при заміні маси кожного типу атомів на їх середнє арифметичне (m + M)/2, частоти цих коливань повністю співпадають. Поблизу центра зони Бріллюена частота пропорційна довжині хвильного вектора – ω ~ q. Крім того, підставивши (2.13) у систему (2.10) можна знайти співвідношення між амплітудами коливань сусідніх атомів – А_е = А_о, тобто вони коливаються у однаковій фазі з однаковими амплітудами (рис. 2.5 а). Такі коливання можуть збуджуватись генератором звуку шляхом створення змінного тиску на кристал і тому називаються акустичними; вони містять увесь спектр звукових коливань ланцюжка. Далі буде показано, саме ці коливання визначають теплові властивості кристалів – їх теплоємність, теплопровідність, теплове розширення і т. п.

Рис. 2.5. Залежність від довжини хвильового вектора q частот ω а) акустичної та б) оптичної гілок коливань атомів складної одновимірної ґратки

Розв’язок (2.14) визначає інший, відсутній у простому кристалі, тип хвиль. По-перше, частота коливань у хвилі цього типу – слабко спадна функція. Поблизу центра зони Бріллюена вона практично не залежить від довжини хвилі і становить величину, близьку до . При наближенні до країв зони вона слабко спадає до значення . Підстановкою (2.14) у (2.10) можна знайти співвідношення між амплітудами коливань сусідніх атомів – у випадку довгих хвиль , тобто вони коливаються у протилежних фазах з різними амплітудами (рис. 2.5 б). Такої поведінки можна очікувати від системи зарядів протилежних атомів, розташованих почергово у ланцюжку при дії на неї змінного повздовжнього електричного поля. Коливання цього типу можуть поширюватись, наприклад, у кристалічній ґратці іонного кристалу внаслідок дії змінного електричного поля, напрямленого вздовж його осей. Таким може бути поле зовнішньої електромагнітної хвилі, тому коливання цього типу можуть викликатись дією світла. З цієї причини їх називають оптичними. Коливання такого типу визначають оптичні властивості кристалів.

Оптичні коливання можуть поширюватись і у випадку складної ґратки, яка складається з атомів одного сорту. Тут вони виникають внаслідок коливань однієї з підґраток відносно іншої.

Графік залежності ω(q) для складної одновимірної ґратки показаний на рис. 2.6 для випадку M >> m. Характерною його особливістю є наявність двох гілок – акустичної і оптичної, – а також щілини – інтервалу заборонених значень частоти ( ). Коливання з частотами з цього інтервалу не можуть поширюватись у ґратці без згасання. Існування аналогічних заборонених зон ми побачимо і в енергетичному спектрі електрона у кристалі.

На завершення звернемо увагу на те, що скінченність розмірів кристалу тут також накладає необхідність квантування дозволених значень хвильового вектора і, відповідно, частот коливань (акустичних і оптичних).