Поглощения
X • ( X + Y) = X
В результате получается неубывающая (тупиковая) БФ. Её реализаций может быть множество, но применяется та, которая требует меньшего количества логических элементов.
П
ример:
_ _ _ х + х
+ х = х _
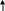
Дано:
F = ABC + ABC + ABC + ABC; + [ABC
+ ABC] = BC(A+A)+
_ _ добавочные
AC(B+B) + AB(C+C) = BC + AC + AB. элементы
Результат: Количество выходных элементов уменьшилось с 4→ 3.
На основе рассмотренных логических схем осуществляется функционирование практически всей цифровой электронно-вычислительной техники.
Алгебра высказываний, исчисление высказываний
Повествовательное предложение, записанное на естественном или формализованном языке, для которого имеет смысл говорить о его истинности или ложности, называется высказыванием. Другими словами, высказывание – это предложения, которые могут принимать значения “истина” - 1, или “ложь” - 0. Пример: 5>10 - ложно; 5<10 - истинно.
Высказывания представляют булевыми константами (булевыми переменными 0,1), в дальнейшем обозначаемыми малыми буквами латинского алфавита. Такие высказывания называют элементарными (простыми).
Подставляя элементарные высказывания в формулы для булевых функций, конструируем составные высказывания. Они обозначаются большими буквами латинского алфавита.
Составное высказывание называется тождественно истинным (ложным) или тавтологией (противоречием), если оно истинно при всех значениях входящих в него элементарных высказываний.
В аксиоматической теории исчисления высказываний под высказыванием понимается формула для булевой функции, но понятие “истина” (тавтология) не определяются. Вместо них задаётся набор некоторых высказываний, объявленных аксиомами. Из аксиом и исходных высказываний (допущений), с помощью правил вывода строится последовательность высказываний, называемая выводом из допущений. Этот вывод из допущений называется доказательством, а высказывание в его конце – формально доказуемым или теоремой (╞). Выводимые и доказуемые высказывания являются истинами “аксиоматической” теории. Выбирая аксиомы и различные выводы можно построить различные логики.
Среди булевых функций можно выделить функции, остающиеся истинными, вне зависимости от значений входящих в них элементов. Такие функции называются универсально истинными или тавтологиями5.
Тавтологиями являются основные правила алгебры логики:
Х + 0=Х. 2) Х + 1=1. 3) Х+Х+Х=Х. 4) Х+ неХ = 1. 5) Х·0=0.
6)X · 1 = X. 7) Х·Х·Х = Х. 8) Х умножить на не Х=0. 9) Х = Х.
Примеры:
1. Доказать табличным способом соотношения
_____ _
a \/ b = ā /\ b
a b |
a \/ b |
___ a \/ b |
ā |
_ b |
_ ā /\ b |
0 0 |
0 |
1 |
1 |
1 |
1 |
0 1 |
1 |
0 |
1 |
0 |
0 |
1 0 |
1 |
0 |
0 |
1 |
0 |
1 1 |
1 |
0 |
0 |
0 |
0 |
2. Доказать теорему: ╞ (a → b) → (c \/ a) → (c \/ a).
Используем сокращённую таблицу истинности с учетом высказываний: b = ā + b; a ~ b = (a → b) /\ (b → a).
a |
ā |
a \/ b |
a /\ b |
a → b |
b → a |
a ~ b |
0 |
1 |
b |
0 |
1 |
не b |
не b |
1 |
0 |
1 |
b |
b |
1 |
b |
a = 0 a = 1
(0 → b) → ( c \/ 0 → c \/ b) (1 → b) → (c \/ 1 → c \/ b)
1 → ( c → c \/ b ) b → (1 → c \/ b)
c = 0 c = 1 b = 0 b = 1
0 → 0 \/ b 1 → 1 \/ b 0 → 0 \/ c 1 → c \/ 1
1 1 1 1
Таким образом, высказывание становится истинным, так как истинны все входящие в него высказывания, и можно преобразовывать выражения естественного языка на логический язык:
_____ _ _ ____ _ _ _
А \/ В = А /\ В А /\ В = А \/ В А → В = А \/ В