9. Правила кирхгофа для разветвленных

ЦЕПЕЙ.

Любая точка разветвления цепи, в которой сходится не менее трех проводников, называется узлом. Ток, входящий в узел — положительный, а ток, выходящий — отрицательный.

Первое правило Кирхгофа:

Алгебраическая сумма токов, сходящихся в узле, равна нулю: I_i = o.

Второе правило Кирхгофа получается из обобществленного закона Ома для разветвленных цепей. Возьмем контур, состоящий из трех участков (рис. 1). Направление обхода контура по часовой стрелке — положительное, отметив, что выбор направления совершенно произволен. Все токи, совпадающие по направлению с направлением обхода контура, считаются положительными, а не совпадающие с направлением обхода - отрицательными. Источники Э.Д.С. считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к участкам контура закон Ома,

I₁R₁ = _A - _B + E_{1 ,} - I₂R₂ = _B - _C - E₂, I₃R₃ = _C - _A + E₃

Складывая по членно эти уравнения, получим

I₁R₁ - I₂R₂ + I₃R₃ = E₁ + E₂ + E₃

Второе правило Кирхгофа:

В любом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил тока I_i на сопротивления R_i соответствующих участков этого контура равна алгебраической сумме Э.Д.С. встречающихся в этом контуре: I_iR_i = E_i.

При расчете сложных цепей постоянного тока с применением правил Кирхгофа необходимо:

1. Выбрать одно направление токов на всех участках цепи.

2. Выбрать одно направление обхода контура и строго его придерживаться.

3. Составить столько уравнений, чтобы их число было равно числу искомых величин: каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах.

Методика и техника эксперимента.

Для точного измерения сопротивлений применяют электрическую схему, называемую мостом Уитстона. Эта схема представлена ниже.

R ₁, R₂, R₃, R₄ – четыре сопротивления, образующих плечи моста, G – чувствительный гальванометр, ε – источник тока. Сопротивления плеч подбирают таким образом, чтобы ток через гальванометр был равен нулю. В этом случае говорят, что мост находится в равновесии. Условие равновесия моста можно получить, используя правила Кирхгофа. Так как ток через гальванометр равен 0, то применяя первое правило Кирхгофа к узлам В и D, можно записать:

I₁ = I₂, I₃ = I₄. (1)

Применяя второе правило Кирхгофа к контурам АВD и ВСD, получим:

I₁R₁ – I₃R₃ = 0,

I₂R₂ – I₄R₄ = 0,

или, используя (1): I₁R₁ = I₃R₃ (2)

I₂R₂ = I₄R₄. (3)

Разделив почленно равенства (2) и (3) и используя (1), получим условие равновесия моста

. (4)

Из уравнения (4) можно определить любое из четырех сопротивлений, включенных в плечи, если известны три других сопротивления.

Экспериментальная установка, используемая в данной работе показана ниже:

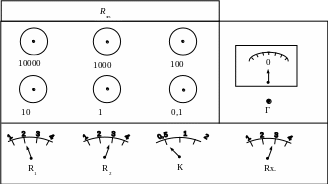
R₁, R₂ – неизвестные сопротивления; R_эт – магазин сопротивлений; Г – гальванометр.

Сопротивления R₃ и R₄ подобраны таким образом, что их отношение равно: 0,5; 1; 2 Ом.

= k, где k = 0,5; 1 и 2.

Неизвестное сопротивление R_х может быть выражено через соответствующие сопротивления трех остальных плеч моста:

R_х = R_эт · , так как отношение = k, то

R_х = k·R_эт. (5)

Порядок выполнения работы