РОЗДІЛ 3. Диференціальне числення

ТЕМА 1. ФУНКЦІЇ. ОБЛАСТЬ ВИЗНАЧЕННЯ.

ЕЛЕМЕНТАРНІ ФУНКЦІЇ

§1. Повторення і розширення відомостей про функції

1. Означення функції. Зростаючі, спадні, парні і непарні функції. Матеріальна єдність світу виявляється у взаємозв`язку і взаємо обумовленості різних явищ і процесів, що відбуваються в природі. Розглядаючи їх, доводиться враховувати залежності одних змінних від інших. Наприклад, залежність шляху від часу, залежність кількості купленого товару на певну суму від ціни, залежність між площею круга і його радіусом. Необхідність вивчення на практиці залежностей між змінними різної природи привела до поняття функції в математиці. Поняття функції є центральним для всієї математики. Особливо важливу роль вона відіграє в математичному аналізі. Перед тим як дати визначення для функції, розглянемо наочний приклад.

Припустимо, що деяка фірма виробляє продукцію, яку продає по ціні 100 гр. од. за одну штуку (в подальшому конкретний вид продукції та наіменування грошових одиниць будемо опускати). Далі припустимо, що в нас є таблиця, в яку занесено дані про щоденний продаж та доход:

Об`єм продажу (шт.. в день)	30	40	28	14	36
Доход (гр.од.в день)	3000	4000	2800	1400	3600

Неважко зрозуміти зміст цієї таблиці. Якщо, наприклад, в день продано 30 одиниць продукції, то доход за цей день складатиме 3000, якщо 40, то 4000 і.т.д. Позначивши денний об`єм продажу через x , а відповідний доход через y, можна зв`язок між ними виразити простою формулою: y = 100x

Тепер дамо загальне означення функції.

Функцією f, заданій на деякій множині X , називається правило, за яким кожному елементу x  X ставиться у відповідність один і тільки один елемент y  Y.

Функцію позначають або однією літерою латинського алфавіту f, F, або за допомогою рівності у = f(x), яка символічно означає залежність між двома змінними.

Змінну х називають незалежною, або аргументом, а змінну у – залежною. Значенням функції називають значення залежної змінної у, якого вона набуває за деякого певного значення х.

Множина значень, яких набуває незалежна змінна х, називається областю визначення функції. Позначають D(x) або Х.

Множина відповідних значень залежної змінної у, яких вона набуває при всіх значеннях х з області визначення функції, називається областю значень, або областю зміни функції. Позначають Е(у) або У. В алгебрі і початках аналізу окремо означається число­ва функція:

Числовою функцією з областю визначення Х називається залежність, при якій кожному числовому значенню х з множини Х ставиться у відповідність єдине деяке число у з множини У.

Інколи функцію задають різними формулами на різних множинах значень аргументу (так звані «кусково-задані функції»). Наприклад, якщо турист був у дорозі 9 год. і перші 5 год. рухався зі швидкістю 4,5 км/год, потім відпо­чивав 0,5 год. а решту часу йшов зі швидкістю 4 км/год, то функцію шляху s залежно від часу t запишемо у вигляді

Функція у = f (x) називається зростаючою, якщо біль­шому значенню аргументу відповідає більше значення функ­ції, тобто для будь-яких двох значень x₁ , x₂ змінної х, взятих з області визначення

і таких, що х₂ > х₁, виконується нерівність f (х₂) >f(x₁).

Функція у= f (х) називається спадною, якщо більшому значенню аргументу відповідає менше значення функції, тобто для будь-яких двох значень x₁, x₂, змінної х, взятих з області визначення і таких, що х₂ > x₁ виконується не­рівність f (x₂) < f (x₁).

Алгоритм дослідження функцій на зростання і спадання:

1). Вибрати будь-які два значення x₁ і x₂ з області визна­чення функції такі, що x₂ >x₁;

2). Скласти різницю f(х₂) — f (Х₁) і з'ясувати (якщо це можливо), чи буде вона додатною ( від'ємною ) і, користую­чись означенням нерівності, переконатися, що f (х₂) > f (x₁) (чи f(Х₂) < f (x₁)), а звідси зробити висновок про зростання (спадання) функції.

У зростаючої функції графік піднімається вгору, у спадної — опускається вниз.

Функція у = f(х) називається парною, якщо для будь-якого значення х з області визначення значення (—х) та­кож належить області визначення і виконується рівність f(-x) = f(x). Інакше кажучи, у парних функцій їх значен­ня для протилежних значень аргументу рівні. Графік пар­ної функції симетричний відносно осі ОУ.

Функція у = f(x) називається непарною, якщо для будь-якого значення х з області визначення значення (— х) також належить області визначення і виконується рів­ність f(-x ) = - f(x). . Графік непар­ної функції симетричний відносно початку координат..

2. Основні види функцій:

1).Лінійна: у = кх+в.

Наприклад: а). вартість N телеграми з Києва в Чернівці обчислюється за формулою N = 60x + 1000, де х- кількість слів, 60 коп. вартість одного слова, 1000 коп. кур`єрська оплата; в). вартість проїзду в таксі можна обчислити за формулою Р = 4n + 4, де n – кількість кілометрів (відстань), що проїхав пасажир, 4 грн. – вартість проїзду одного кілометра, 4 грн. сума, яка автоматично фіксується на лічильнику, коли пасажир сідає в таксі (ціни умовні).

2). Обернено пропорційна ,це функція, яку можна задати формулою , де х- незалежна змінна і число . Функція виражає , наприклад, залежність кількості купленого товару на задану суму грошей від ціни товару.

3). Степенева функція у = х^ . Вигляд степеневої функції суттєво залежить від природи числа 

4). Функції : а) ціла частина числа у= і б) дробова частина числа у= .

Кожне дробове число можна подати у вигляді суми двох доданків, один з яких ціле число, а другий - невід`ємний правильний дріб.

Наприклад: 10,7 = 10 + 0,7;

0,5 = 0 + 0,5; - 2,25 = - 3 + 0,75.

Ціла частина числа х - це найбільше ціле число, яке не перевищує х.

Цілу частину числа х позначають символом , де х = n + q,

n Z, а 0 q<1.

Очевидно, що = n. При будь-якому х виконується подвійна нерівність <

Формула - ціла частина х, задає функцію, областю визначення якої є множина всіх дійсних чисел.

Г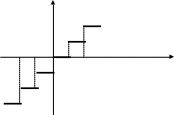 рафік функції . У

2

1

-3 -2 -1 0 1 2 3 Х

-1

-2

-3

Дробовою частиною числа х називається різниця між цим числом і його цілою частиною. Дробову частину числа х позначають . З означення випливає, що = .

Наприклад:

Формулою , або задається функція,областю визначення якої є множина всіх дійсних чисел.

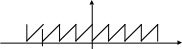у

1

-4 -3 -2 -1 0 1 2 3 х

Способи задання функцій.

• Аналітичний ( за допомогою формули).

Наприклад : y = 100x; у = х²; y = sinx.

• Табличний (див. попередній приклад).

• Словесний. Наприклад: у - ціла частина числа х

• Графічний.

Основні позначення

х - незалежна змінна

у - залежна змінна

D(y) - область визначення

Е(у) множина значень

y = f(x) - позначення функції