3. Связь фокусного расстояния с показателем преломления стекла и радиусами кривизны линзы. Оптическая сила линзы.

1/a₂ - 1/a₁ = (N - 1) (1/R₁ - 1/R₂), (2.14)

где N = n/n₁ - показатель преломления материала линзы отно­сительно окружающей среды (относительный показатель прелом­ления). Формула (2.14) является формулой тонкой линзы и верна как для выпуклых, так и для вогнутых линз при произвольном расположении точки М. При a₁ = - ∞ получим

(2.15)

При a₂ = ∞ имеем

(2.16)

Как видно, fi = -f ₂, т.е. фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Знак минус показывает, что фокусы расположены по разные стороны от линзы.

Исходя из выражений (2.14) и (2.16), формулу линзы можно -написать в более простом виде:

1/a₂ – 1/a₁ = 1/f₁ (2.17)

Применяя эту формулу для разных случаев, можно получить из нее конкретные результаты. При работе с формулами (2.14) и (2.17) не следует забывать, что величины справа от линзы положительные, слева - ­ отрицательные.

Величина, обратная главному фокусному расстоянию f' пространства изображений, взятая с противоположным знаком, т. е. -1/f', называется оптической силой системы. Оптическая сила измеряется диоптриями. Диоптрия есть оптическая сила та­кой системы, фокусное расстояние |f’| которой равно одному метру. Для собирательных тонких линз оптическая сила положи­тельна, для рассеивающих отрицательна.

4. Поперечное увеличение линзы

Отношение у'/у называется поперечным увеличением, или просто увеличением системы.. Согласно формулам или, оно не зависит от у и z. Отсюда следует, что изображение плоского предмета, перпендикулярного к главной оптической оси, подобно самому предмету. Если увеличение положительное, то изображение прямое. В противоположном случае изображение обратное.

5. Фокусное расстояние центрированной системы двух тонких сферических линз.

Определим оптическую силу сложной системы, зная оптические силы составляющих систем и их взаимное расположение. Будем предполагать, что показатели преломления всех пространств пред­метов и изображений одинаковы. Обозначим через l₁₂ расстояние H’₁H₂ передней главной плоскости H₂ второй системы от задней главной плоскости Н’₁ первой системы. Оптический интервал между рассматриваемыми системами будет

Δ = F’₁F₂ = F’₁H’₁+ H’₁Н₂ + H₂F₂ = f’₁ +l₁₂ – f₂ = f’₁ +l₁₂ – f’₂.

Подставляя это значение в формулу (12.3), получим

(2.18)

В частности, когда задняя главная плоскость первой системы совпа­дает с передней главной плоскостью второй системы,

, (2.19)

т. е. оптическая сила сложной системы равна сумме оптических сил составляющих систем. Это имеет место, например, для двух тон­ких линз, прижатых вплотную одна к другой.

6. Аберрации линз.

П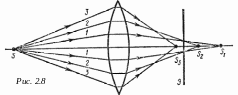 ри построении изображения малого предмета в тонкой линзе мы пользовались параксиальным пучком света. Кроме того, лучи параксиального пучка составляли небольшие углы с главной опти­ческой осью. Далее, падающий свет считали монохроматическим, а показатель преломления материала линзы - не зависящим от длины волны падающего света. На практике все эти условия не соб­людаются и возникают соответствующие недостатки оптических систем. Коротко остановимся на некоторых из них.

С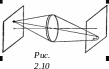 ферическая аберрация. В случае тонкой линзы параксиальный пучок, исходящий из точки S, после преломления в линзе пересекает оптическую ось в одной точке. Если же пучок света, исходящий из источника S, составляет большой угол с главной оптической осью, то лучи, составляющие разные углы, пересекают оптическую ось не в одной точке, а в разных точках, например точки s₁, s₂, s₃ на рис. 2.8. Лучи, более удаленные от центра линзы, сильнее преломляются и пересекают главную оптическую ось на сравнительно близких расстояниях от центра линзы. Если экран Э, рас­положенный перпендикулярно главной оптической оси, перед­вигать влево от s₁ к s₂, то вместо стигматического точечного изобра­жения получается расплывчатое пятно. Такая погрешность, связан­ная со сферичностью преломляющих поверхностей, называется сферической аберрацией. Для количественной характеристики сферической аберрации вводится понятие продольной аберрации, равной линейному расстоянию точки пересечения крайних (лучи 3 на рис. 2. 8) и центральных (лучи 1) лучей пучка с главной оптичес­кой осью (S₃S₁). Линейная аберрация зависит от материала линзы, от кривизны поверхностей. Продольные аберрации собирательной и рассеивающей линз противоположны по знаку. Это позволяет, комбинируя такие линзы, уменьшить сферическую аберрацию.

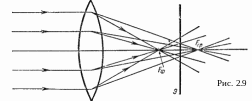
Хроматическая аберрация. Из-за явления дисперсии (зависи­мость показателя преломления от длины волны) для данной линзы фокусы для разных цветов будут смещены друг относительно друга (на рис. 2.9 показаны фокус F_ф для фиолетовых и фокус F_кp для красных лучей). В результате этого изображение белого пятна получается цветным. Чередование цветов зависит от положения экрана наблюдения, а соответствующее искажение носит название хроматической аберрации. Хроматическая аберрация, подобно сферической, количественно характеризуется продольной хроматической аберрацией (F_фF_кр). Для сведения по возможности к мини­муму хроматической аберрации пользуются комбинацией линз, изготовленных из специально подобранных материалов. Такая система называется - ахроматической. Ахроматические системы, безусловно, не могут полностью устранить хроматическую абер­рацию. Самая простая ахроматическая система состоит из выпуклой линзы, изготовленной из кронгласа (легкого сорта стекла) и при­клеенной к двояковыпуклой линзе из флинтгласа (тяжелого сорта стекла). Прибавление рассеивающей линзы к системе приводит к увеличению ее фокусного расстояния. Однако такое увеличение фокусного расстояния зависит от длины волны, причем фокусное расстояние для фиолетового света увеличивается больше, чем фо­кусное расстояние для красного света. Обычно при изготовлении ахроматической системы расчет производится так, чтобы фокусы для двух и более длин волн совпали. В случае визуального наблюдения добиваются совпадения фокусов для длин волн λ = 6563 А (красный) и λ = 4861 А (голубой). При фотографировании ахрома­тическая система подбирается так, чтобы совпали фокусы для длин волн λ = 4341 А и λ = 5893 А. Такой выбор длин волн обусловлен тем, что са­мое сильное воздействие на фотоплас­тинки оказывают именно эти цвета.

Дисторсия изображения. В случае, когда лучи, участвующие в построении изображения, образуют достаточно большие углы с главной оптической осью, увеличение системы зависит от угла между пучком и главной оптической осью. В этом случае изображе­ние не является подобным предмету. Это обусловлено тем, что отношение тангенсов углов поля зрения и поля изображения не является постоянной величиной для точек по всему полю изображения. Поэтому н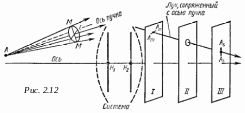 апример, предмет в виде правильного квадрата изобра­жается в искаженном виде — в виде подушки, бочки или еще более сложной фигуры. Недостатки такого рода называются дисторсией. Соответствующий подбор составленных ч астей оптической системы позволяет сделать исправление на дисторсию. Оптическая система, свободная от дисторсии, называется ортоскопической.

Кома. Кривизна поверхности оптических систем кроме сфери­ческой аберрации вызывает также и другую погрешность — кому (рис. 2.10). Лучи, идущие от точечного объекта, лежащего вне оп­тической оси системы, образуют в плоскости изображения в двух взаимно перпендикулярных направлениях сложное несимметрич­ное пятно рассеяния, напоминающее по виду комету с хвостом. Поэтому подобная аберрация во внеосевых пучках была названа комой. На рис. 2.10 представлено несимметричное пятно рассеяния в так называемой сагиттальной (перпендикулярной к оптической оси) плоскости. Кома обусловлена, как выше отметили, как сферич­ностью поверхности, так и удаленностью точки от оси, в результате чего построение изображения производится внеосевыми (наклон­ными) пучками. Действительно, при той же сферической поверх­ности в осевом пучке, вверх и вниз от оптической оси, существует полная симметрия в отношении преломления. В случае же наклон­ного пучка ввиду полного отсутствия подобной симметрии верхние и нижние части преломляются по-разному и в итоге получают различ­ные погрешности.

Кома является одной из наиболее существенных аберраций. Поэтому, подбирая соответствующие совокупности частей оптической системы, нужно свести ее к минимуму. У системы с исправленной сферической аберрацией кома отсутствует, если для нее удовлетво­рено условие синусов Аббе. Если в оптической системе полностью устранены кома и сферическая аберрация для всего отверстия и всех наклонов лучей, то монохроматический свет в данной системе образует идеальное изображение, лишенное всех недостатков.

Астигматизм наклонных пучков. Астигматизм наклонных пучков (рис. 2.12) заключается в том, что лучи одного и того же пучка, исхо­дящие из точки и идущие в двух взаимно перпендикулярных плоско­стях, после преломления в оптической системе, теряя гомоцентричность, не собираются в одну точку, а образуют две точки схода. Представим себе пучок лучей, исходящий из точки А и падающий на оптическую систему под углом к ее оси. Рассмотрим лучи, как бы выделенные крестообразной узкой диафрагмой, кресты которой направлены по меридиональной и сагиттальной плоскостям. Из такой диафрагмы выйдет плоская ленточка лучей, расположенных (при соответствующей ориентации крестов диафрагмы) в меридио­нальной и сагиттальной плоскостях. Эти ленточки лучей из-за раз­личия кривизны по двум взаимно перпендикулярным направле­ниям преломляются по-разному, и в результате изображением точки А являются две линии на двух взаимно перпендикулярных фокальных плоскостях. Линия A_SA_S образуется в результате пре­ломления сагиттальных лучей и ориентирована в меридиональной плоскости, а линия А_тА_т образуется при преломлении меридио­нальных лучей и ориентирована в перпендикулярной плоскости (рис. 2.12). Эти две фокальные плоскости расположены на разных расстояниях от главной плоскости системы. Если изображением точки А в плоскости / служит линия А_тА_т, а в плоскости /// — линия A_SA_S, перпендикулярная линии А_тА_т, то это изображение при перемещении от плоскости / к плоскости /// превращается в фигуры рассеяния в виде эллипсов различного эксцентриситета. Фигура рассеяния только в одной плоскости, расположенной по­середине между плоскостями / и ///, имеет вид круга (//).

Следо­вательно, и в случае астигматизма наклонных пучков изображение точки имеет вид пятна рассеяния, форма которого, как следует из вышеизложенного, зависит от положения экрана наблюдения.

Астигматизм оптической системы может быть исправлен путем подходящего подбора радиусов кривизны преломляющих поверх­ностей и их фокусных расстояний. Оптическая система, свободная от астигматизма, называется анастигматом.

Исправление всех недостатков оптической системы одновременно практически невозможно. В каждом конкретном приборе устраня­ется тот или иной недостаток в зависимости от предназначения данного прибора.