Признаки сходимости
Необходимый признак сходимости:
Если
сходится,
то общий член
Доказательство: Пусть - n – частичная сумма.
-
число.
При
,
тоже
и
-
n-1
– частичная сумма.
Она имеет предел
.
Т.к
конец доказательства.
Необходимый признак сходимости неудобен на практике, т.к по поведению общего члена Un на бесконечности нельзя судить о сходимости ряда.
На практике удобно пользоваться достаточным признаком расходимости ряда:
Если
не
стремится к 0 при
Примеры:
1)
2)
Числовые ряды с положительными членами
Рассмотрим
знакоположительный числовой ряд
,
где
.Последовательность
частичных сумм такого ряда будет всегда
возрастающей:
На 1 курсе была доказана теорема о том, что: монотонно возрастающая последовательность, ограниченная сверху имеет конечный предел.
- число.
Для знакоположительного
ряда достаточно доказать, что,
последовательность частичных сумм
ограничена
сверху числом (возрастание и так есть).
1Й признак сравнения
Дано 2 ряда с
положительными членами
(1)
и
(2)
и начиная с некоторого номера N
выполняется неравенство
,
тогда если (2) сходится
то и (1)
сходится.
Если (1) расходится
то и (2) тоже
расходится,
(ряд меньший сходящегося тоже сходится,
ряд больший расходящегося тоже
расходится).
Доказательство:
Обозначим через
- n
– частичная сумма 1 ряда и
- n
– частичная сумма 2 ряда.
Т.к
.
Пусть 2 ряд сходится, тогда
,
причём
ограничена сверху числом
(1)
сходится.
Пусть 1 ряд расходится
,
т.к
расходится.
Конец доказательство.
Замечание: при доказательстве этого признака мы считали, что неравенство выполняется с 1 номера. Этот факт не влияет на сходимость, т.к по свойству рядов отбрасывание n – первых членов ряда на сходимость ряда не влияет.
Для сравнения необходим стандартный набор рядов, о сходимости всё известно. К таким рядам относятся:
Ряды для сравнения: |
|
Ряды членов геометрической прогрессии:
|
Обобщенно гармонический ряд:
(строгое доказательство будет проведено после интегрального признака сходимости) |
Примеры:
1)
2)
3)
II признак сравнения (предельный)
Дано 2 ряда с
положительными членами
(1)
и
(2)
и
-
число
(1)
и (2) сходятся
и расходятся
одновременно.
Доказательство:
- число по определению предела последовательности:
с
которого
Пусть (2) сходится
, тогда сходится и
Из правой части следует, что (1) ряд меньше сходящегося ряда по 1 признаку сравнения (1) сходится
Пусть (2) расходится
выберем
настолько
малым, чтобы
оставалось >0,
для знакоположительности ряда
- расходится. Из левой части (*)
(1) ряд>ряда расходящегося по I
признаку сравнения (1) ряд расходится.
Конец доказательства.
Примеры:
1)
2)
3)
Признак сходимости Даламбера
Дан ряд с
положительными членами
и
Если
- сходиться
Если
- расходиться
Если
- вопрос о сходимости не решен .
Доказательство:
,
начиная с которого
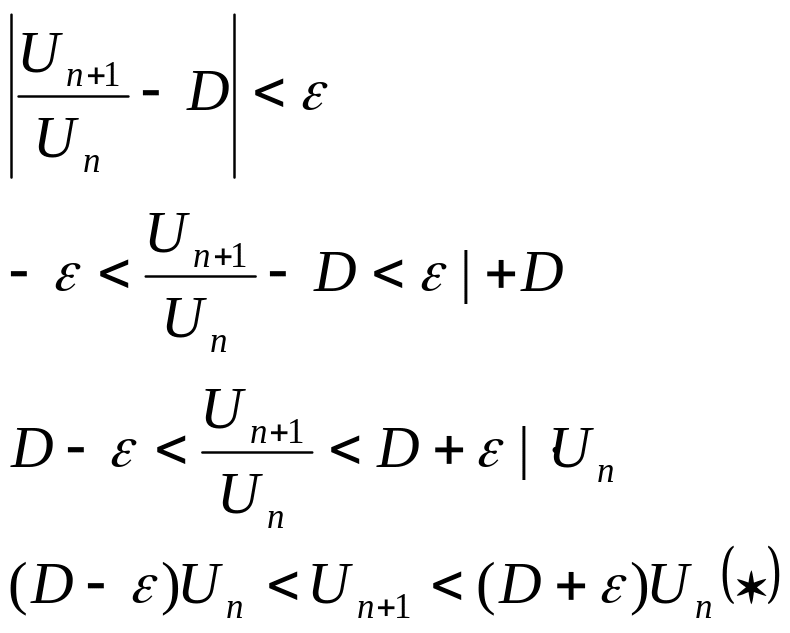
1) Пусть D<1
выберем
настолько
малым, чтобы
обозначим
рассмотрим правую часть
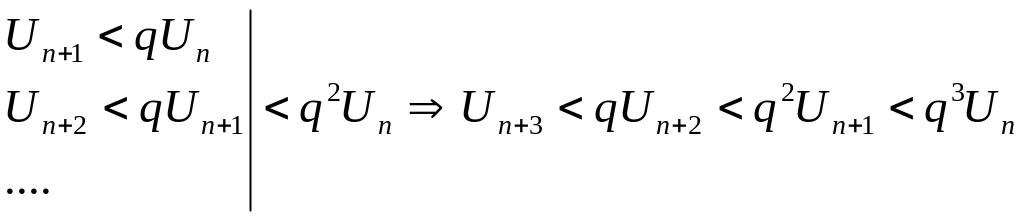
Рассмотрим ряд из
членов геометрической прогрессии
,
т.к ряд q<1
этот
ряд сходится.
Т.к исходный ряд меньше сходящегося ряда из членов меньшего ряда то исходный ряд сходится по I признаку сравнения.
2) Пусть D>1
выберем
настолько
малым, чтобы
>1
<(D-
)
из левой части
>
следовательно члены ряда растут не стремится к 0 , ряд расходится по достаточному признаку расходимости.
3) D=1
Возьмем 2 обобщенно
гармонических ряда
– расходится и
-
сходится.
Для
D=
Для
D=
При D=1 ряд может сходится или расходится и вопрос о сходимости ряда остается открытым.
Конец доказательства.
Примеры:
1)
2)
3)
Радикальный признак Коши.
Дан ряд с
положительными членами
и
Если
- сходиться
Если
- расходиться
Если
- вопрос о сходимости не решен
Доказательство:
по определению
,
начиная с которого
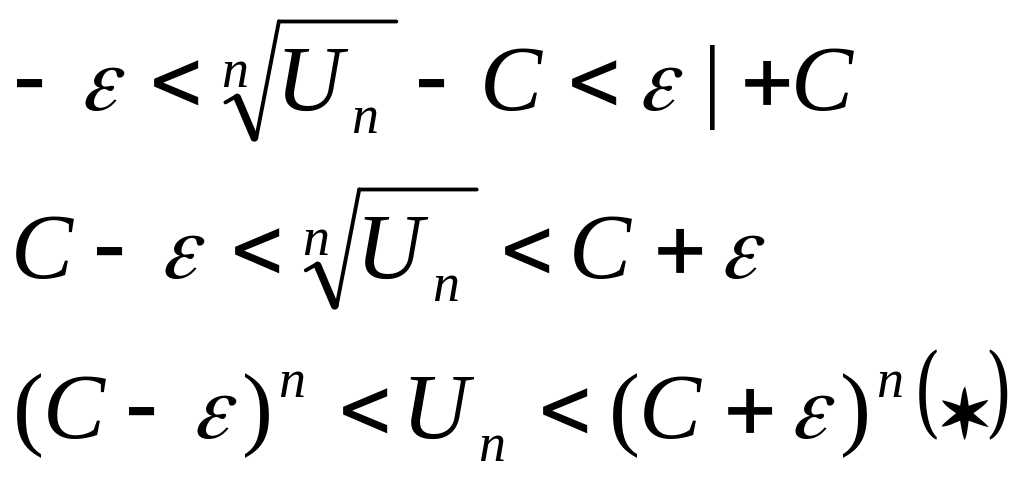
1) Пусть С<1 выберем
настолько
малым, чтобы
,
тогда из правой
части
<
,
ряд
,
где q<1
сходится как ряд из членов геометрической
прогрессии, со знаменателем <1, тогда
исходный ряд сходится по I
признаку сравнения, т.к его члены меньше
членов сходящегося ряда.
2) Пусть С>1 выберем
настолько
малым, чтобы
>1
из левой части
>
;
(q>1)
расходится, как ряд из членов геометрической
прогрессии, расходится по I
признаку сравнения, т.к его члены больше
членов сходящегося ряда.
3)С=1
Возьмем 2 обобщенно гармонических ряда – расходится (p=1) и -сходится (p=2>1) и покажем, что С=1.
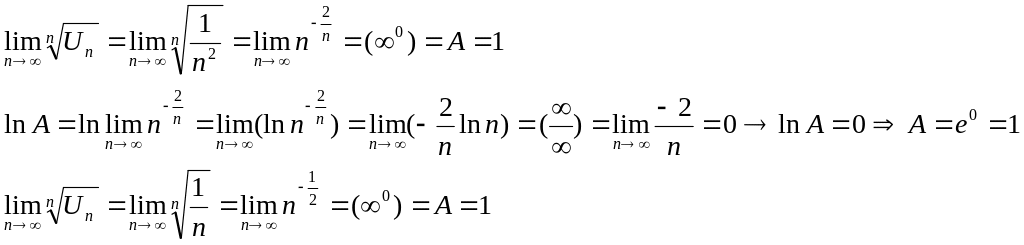
Таким образом при С=1 ряд может как сходится так и расходится.
Конец доказательства.
Примеры:
1)
2)
3)
Интегральный признак Коши.
Дан ряд с
положительными членами
,
что
(
)
и функция f(x)
– положительная и убывающая, связанная
с рядом равенством f(n)=
.
Тогда несобственный
интеграл
и
сходится
и расходится
одновременно.
Доказательство:
f(n)=Un
n
S ступенчатой фигуры над рядом (f(x))
-
n
частичная сумма ряда.
S ступенчатой фигуры под графиком функции f(x)
-
n+1
частичная сумма ряда.
очевидно
неравенство
Пусть несобственный
интеграл
сходится
Из левой части
<числа
-
ограничена сверху числом
-
сходится.
Пусть
расходится
из
правой части (*)
неограничен
ряд
расходится.
Конец доказательства.
Докажем, с помощью интегрального признака Коши, что обобщенно-гармонический ряд:
свяжем с эти рядом несобственный интеграл
(доказано
в несобственном интеграле)
исходный
несобственный интеграл сходится
или расходится
одновременно.
Примеры:
1)
2)
