Линейные неоднородные ду
Это уравнения
вида:
Теорема об общем решении ДУ: Общее решение ДУ(*) имеет вид:
,
где
- общее решение
соответствующего однородного уравнения.
Доказательство:
подставим
в
раскроем скобки и перегруппируемся:
(верно)
Если даны н.у
нужно показать,
что все константы находятся однозначно
,
где ФСР
Продифференцируем
нужное
количество раз и подставим н.у
получим систему
n-линейных
уравнений с n
неизвестными
.
Определитель этой системы
-
определитель Вронского системы функций
.
Т.к
-
ФСР
линейная система имеет единственное
решение и все константы находятся
однозначно.
Конец доказательства.
Замечание: Общее решение соответствующего однородного уравнения
- линейная комбинация
ФСР – известно
Основная трудность нахождения yч – решения неоднородного уравнения.
Линейные неоднородные ду 2 порядка с постоянными коэффициентами со специальной правой частью.
Рассм. ДУ
Общее решение такого уравнения:
,
где
ФСР
-
уже рассматривали
Укажем метод нахождения частного решения неоднородного уравнения
,
если f(x)
имеет специальный вид.
Р
ассмотрим
следующие случаи:
I.
,
где
-
многочлен степени
n.
а)
- не корень характеристического уравнения
,
где
- многочлен степени
n
с неопределенными буквенными
коэффициентами. Подставим
в
ДУ и сравнив коэффициенты при одинаковых
степенях найдём все буквы.
б)
- корень характеристического уравнения
кратности 1
в) - корень характеристического уравнения кратности 2
.
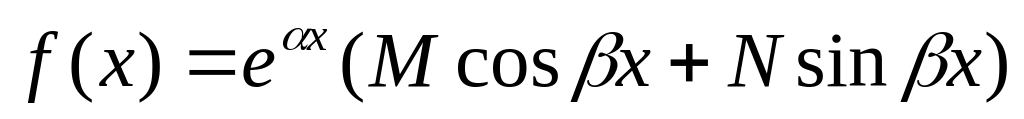,где
M,Nчисла
a)
не корень характеристического уравнения
неопределенные
коэффициенты.Подставив
в
ДУ и приравняв коэффициенты при
находим А и В
б) корень характеристического уравнения кратности 1
|
Замечание : Если
в правой части
есть
только
или
в частном решении должны быть и sin и cos , т.е тригонометрия должна быть полной.
.
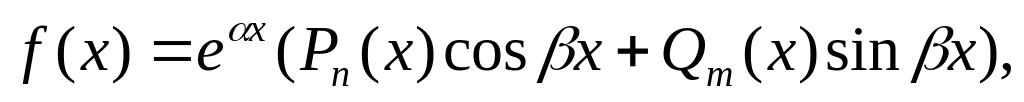
Где
,
-многочлены
степеней m
и n
a)
не корень характеристического уравнения
многочлены
степени к с неопределенными коэффициентами
б)
корень характеристического уравнения
Метод вариации
Рассмотрим ДУ:
Где правая часть f(x) произвольного вида (необязательно специального).
Общее решение соответствующего однородного уравнения:
,
где
и
-
произвольные const,
-
ФСР.
Будем варьировать и и считать, что и зависит от х. Будем искать общее решение неоднородного уравнения (исходного) в виде:
(*)
объединим
и
в
систему
- эта система для
нахождения
и
имеет единственное решение, т.к
определитель системы
,
для системы 2-х ЛНЗ надежнее решать систему по формулам Крамера
,
где
,
где
решая систему получим и , проинтегрируем полученные функции по переменной х.
-
проинтегрируем по х
,
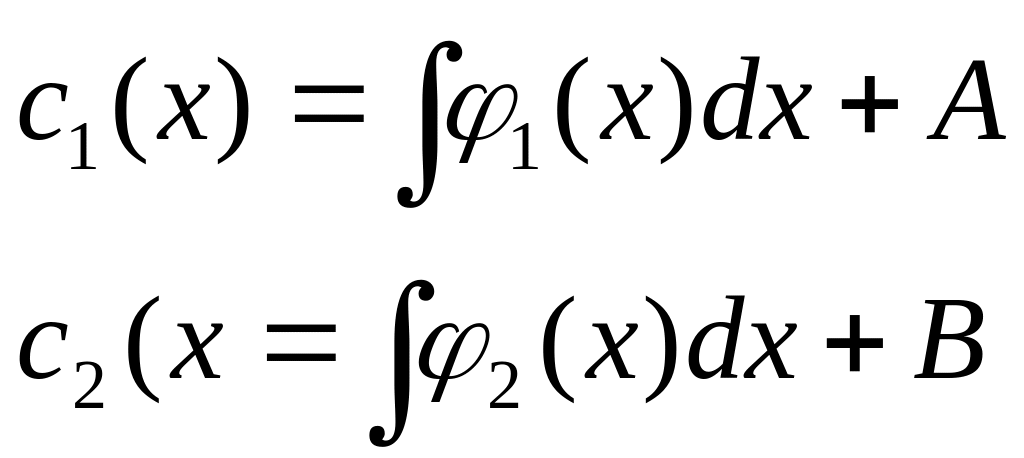где А и В – константы интегрирования
Таким образом общее решение неоднородного уравнения:
Пример:
1)
