Порядок выполнения работы:

1. Составить модельную задачу и отладить на ней программу.

2. Решить задачу для конкретного варианта.

3. Вывести результаты решения модельной задачи для различного числа узлов N в

виде:

4. Вывести результаты для поставленной задачи:

5 Внести случайную погрешность в начальные данные и, проведя вычисления для измененных данных, сделать вывод об устойчивости.

6. Проанализировать результаты.

Примечание. Интегралы (2.14) и (2.15) вычисляются по квадратурным формулам (прямоугольника, трапеции, Симпсона и т.п.).

Типовое задание к лабораторной работе

Решить дифференциальное уравнение

+q(x)u(x) = f(x)

и(a) = и(b) = 0.

Варианты заданий

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

Лабораторная работа №3

Решение дифференциальных уравнений методом Галеркина

Цель работы: решение дифференциального уравнения с помощью проекционного метода Галеркина.

Теоретическая часть

Рассмотрим операторное уравнение

(3.1)

где A – самосопряженный положительно определенный оператор. Введем энергетическое пространство H_A оператора A со скалярным произведением и нормой . Умножим (3.1) скалярно в H на произвольную функцию . Тогда приходим к равенству

(3.2)

Равенство (3.2) допускает уже обобщенную постановку задачи. Обобщенным решением уравнения (3.1) называют функцию , удовлетворяющую соотношению (3.2) при любых .

Сформулируем метод Бубнова-Галеркина.

1) В H_A выбираются базисные функции . Здесь достаточно, чтобы принадлежали H_A, а не D(A).

2) Приближенное решение ищется в виде

. (3.3)

3) Коэффициенты определяются из системы уравнений вида

(3.4)

или в матричной форме, где , , .

Рассмотрим уравнение вида

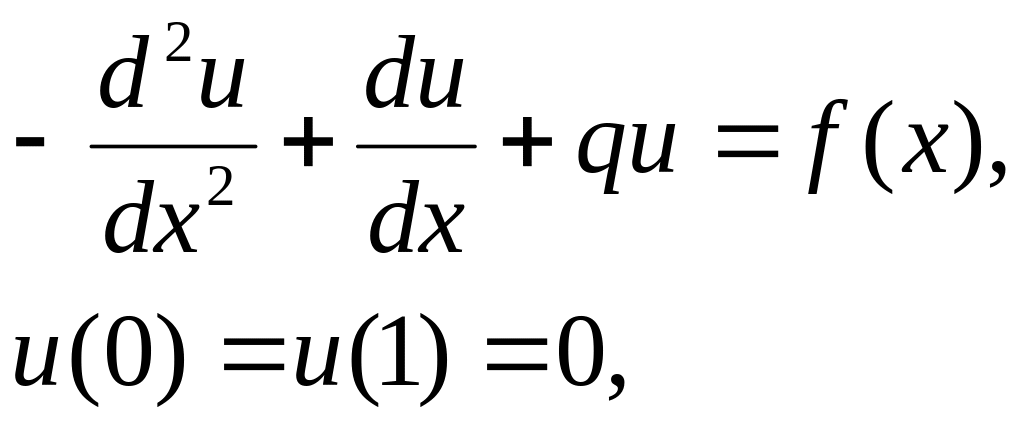(3.5)

или в операторной форме

.

Пространство . Рассмотрим пространство функций 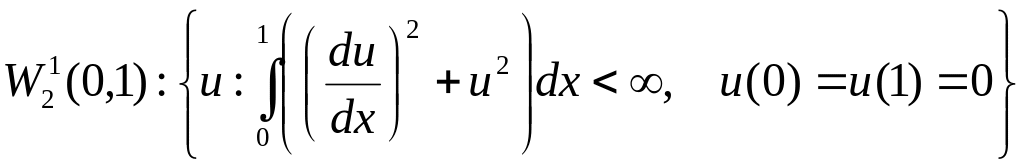. Энергетическое пространство .

Определим скалярное произведение в :

.

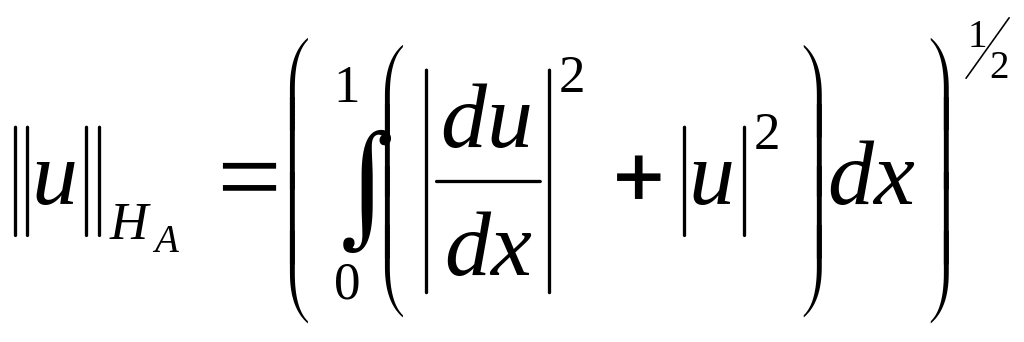Будем искать приближенное решение задачи (3.5) в виде функции , где -система базисных функций.

Коэффициенты определим из системы

,

где ,

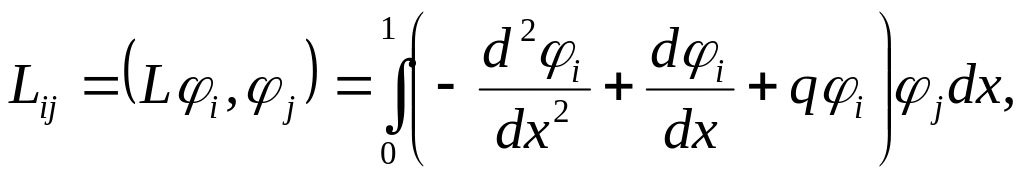
Порядок выполнения работы:

4. Составить модельную задачу и отладить на ней программу.

5. Решить задачу для конкретного варианта.

6. Вывести результаты решения модельной задачи для различного числа узлов N в виде:

4. Вывести результаты для поставленной задачи:

5 Внести случайную погрешность в начальные данные и, проведя вычисления для измененных данных, сделать вывод об устойчивости.

6. Проанализировать результаты.

Типовое задание к лабораторной работе

Решить дифференциальное уравнение

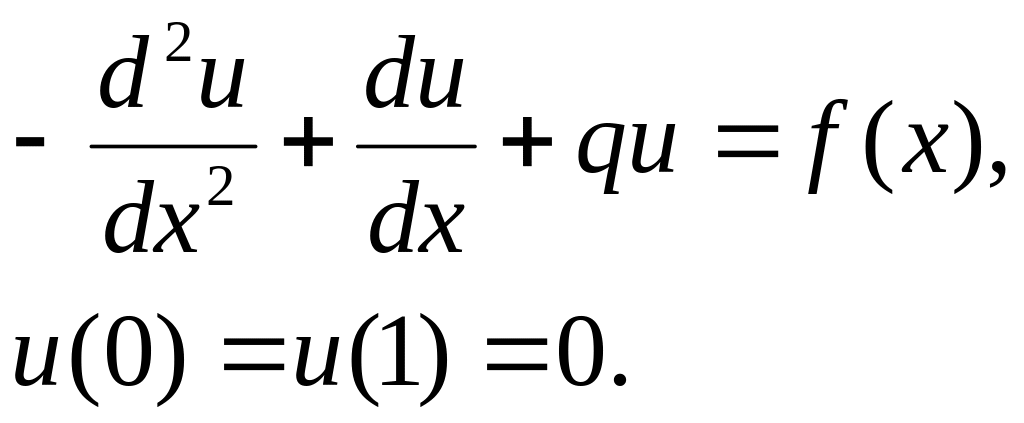
Варианты заданий

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

Лабораторная работа №4

Решение эллиптического уравнения вариационно-разностным методом

Цель работы: решить двумерное эллиптическое уравнение

Теоретическая часть

Рассмотрим двумерную эллиптическую задачу вида

в D, (4.1)

u=0 на , (4.2)

где - ограниченные функции. Граница области D является кусочно-линейной. Эта задача эквивалентна нахождению функции, минимизирующей квадратичный функционал

Предположим, что D = является квадратом. Покроем D обычной равномерной квадратной сеткой с шагом h = , N –целое положительно число.

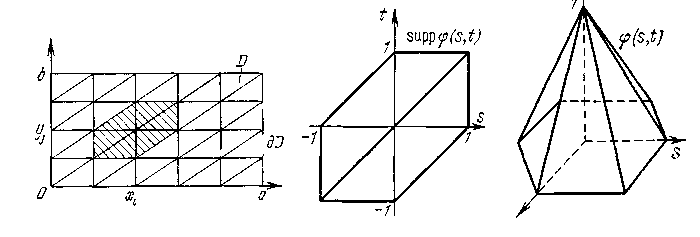
рис.1 рис.2 рис.3

Разобьем D на подобласти D_ij прямыми x_i = ih, у_j = jh, , а затем разделим каждый из прямоугольников D_ij диагональю, как это сделано на рис. 1 (т. е. осуществим триангуляцию области D). Каждому узлу (i,j 1,...,N) поставим в соответствие функцию (х, у), равную единице в данном узле и нулю во всех остальных и линейную в каждом треугольнике. Каждую из этих функций (х, у) для введенной сетки можно выразить через «стандартную» функцию (s, t) вида

Носитель этой функции изображен на рис. 2, а общий ее вид — на рис. 3. Теперь (х, у) можно представить в виде

.

Эти функции часто называют функциями Куранта.

Для построения приближенного решения u^h (x) задачи (4.1), (4.2) воспользуемся методом Ритца с применением базиса . В результате приходим к системе линейных уравнений

= g, (4.3)

где — вектор, составленный из коэффициентов разложения

, (4.4)

— вектор с компонентами

(4.5)

и элементы матрицы вычисляются по формулам

(4.6)

Введем обозначение .

Учитывая вид функций , нетрудно показать, что , если выполнено хотя бы одно из двух неравенств

Отсюда сразу следует, что матрица А является блочной трехдиагональной вида

,

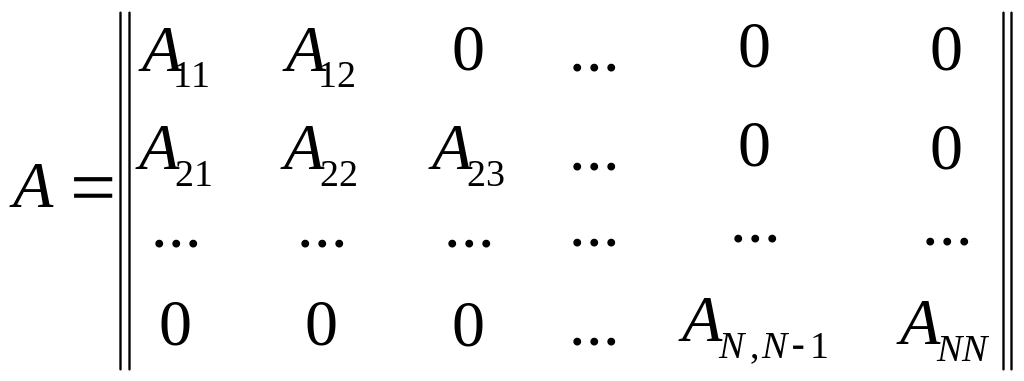где и каждая из матриц является трехдиагональной матрицей порядка N. Более точный анализ показывает, что матрицы — двухдиагональные:

.

Рассмотрим задачу

в D, (4.7)

u=0 на , (4.8)

Можно представить в виде объединения шести треугольников , порядок нумерации которых указан на рис. 5. Непосредственные вычисления показывают, что

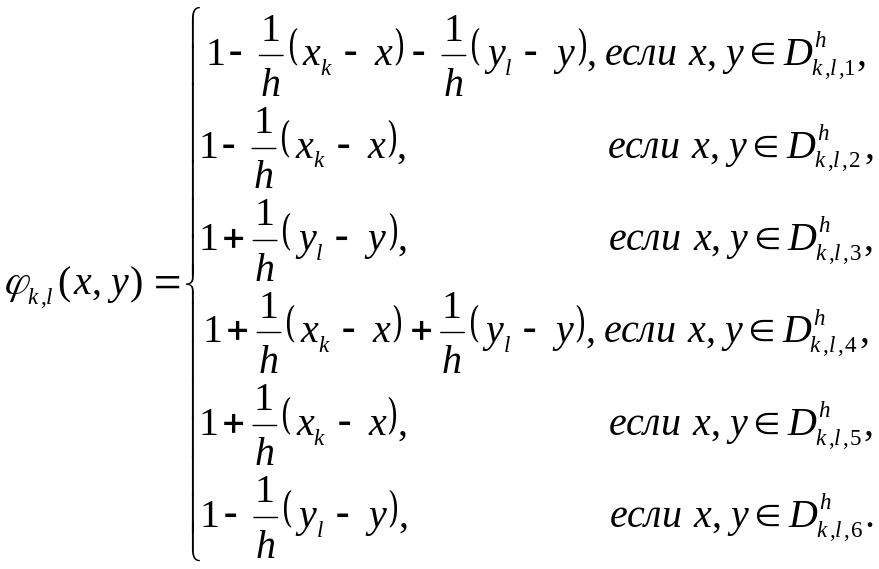(4.9)

В силу симметрии A, трехдиагональности матриц и двухдиагональности матриц и нам достаточно указать формулы для вычисления элементов

, , , ,

Эти формулы, согласно (4.6) и (4.9), имеют вид (для простоты используются обозначения )

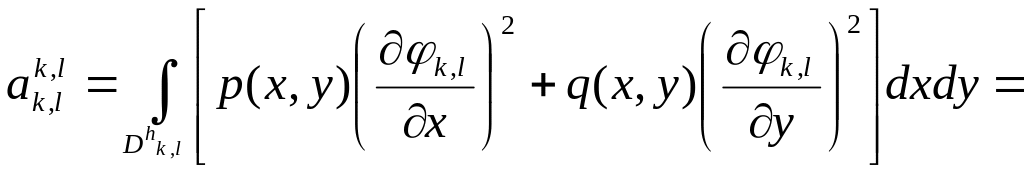
Отсюда следует, что матрицы являются диагональными

рис.4

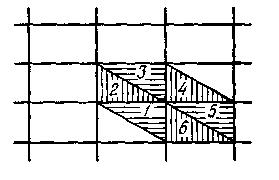
рис.5