3. Метод інтегрування частинами

Даний метод ґрунтується на формулі інтегрування частинами:

або , (12)

де , – неперервно диференційовані функції.

Існують функції, інтегрування яких можливе лише методом інтегрування частинами. Як правило, інтеграл записується у вигляді . Тому в методі інтегрування частинами важливим є вміння правильно подати підінтегральний вираз у формі так, щоб інтеграл був не складнішим за .

Нехай – многочлен -го степеня. Розглянемо різні типи інтегралів, до яких застосовується метод інтегрування частинами та відповідний вибір функцій та .

I. Інтеграли вигляду

1. ; 2. ; 3. ; 4. .

В кожному з цих інтегралів приймаємо . Тоді ,

де – многочлен -го степеня. За приймаємо в кожному з цих інтегралів відповідно:

1. . 2. .

3. . 4. .

Враховуючи це, інтеграли 1–4 можемо тепер записати так:

1. .

Тут інтеграл справа є простішим від інтегралу зліва тим, що в ньому під інтегралом є многочлен степеня . Застосувавши формулу інтегрування частинами разів прийдемо до інтеграла від .

2.

3.

4.

В інтегралах 2, 3 і 4 формулу (12) потрібно застосувати разів.

Приклад 3. Знайти інтеграл . Для скорочення записів тут і надалі в дужках будемо записувати відповідні заміни

.

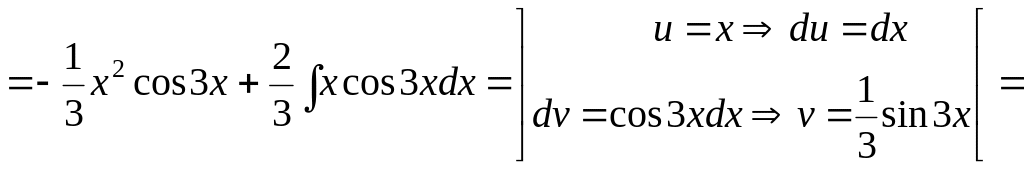
II. Інтеграли вигляду

1. ; 2. ;

3. ; 4. ;

В кожному з цих інтегралів приймаємо , тоді – многочлен -го степеня. За приймаємо в кожному з цих інтегралів відповідно:

1. . 2. .

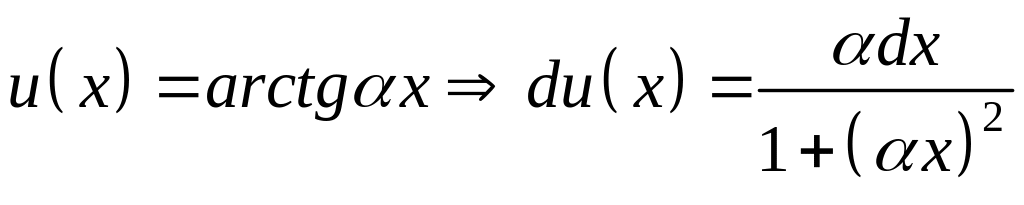3. . 4. .

Приклад 4. Знайти інтеграл .

При обчисленні цього інтеграла використано табличний інтеграл 21 з таблиці Б.

Аналогічно знаходимо і інтеграл .

III. Інтеграли вигляду

1. ; 2. ; 3. ; 4. .

При інтегруванні цих інтегралів формулу (12) застосовуємо двічі. В резуль-таті отримуємо рівняння, з якого знаходимо шуканий інтеграл. В перших двох інтегралах приймаємо . За приймаємо:

1. . 2. .

В інтегралах 3, 4. Вибір множників і є довільним. Наприклад в 3. Можна вибрати і так: , ,

або , .

Приклад 5. Знайти інтеграл .

.

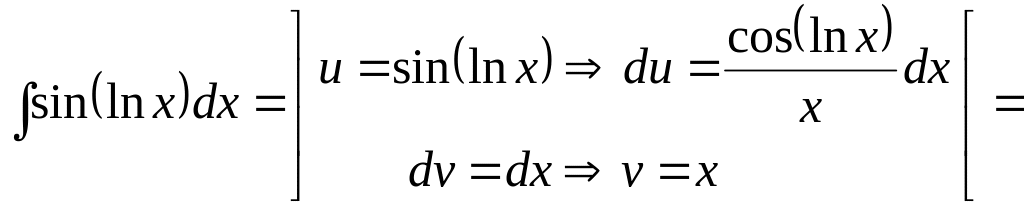
Ми отримали рівняння відносно шуканого інтеграла . Звідси .

IV. Рекурентні формули

Метод інтегрування частинами дозволяє отримати рекурентні формули для інтегралів. Нехай .

Приклад 6. Отримаємо рекурентну формулу для інтеграла , який буде використано при розгляді питання інтегрування раціональних функцій.

Покладемо в цьому інтегралі , . Тоді , .

Тому

.

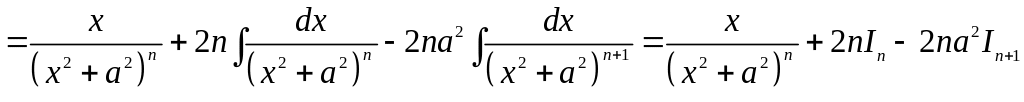Отже, . Звідси знайдемо :

.

Отримана рекурентна формула зводить обчислення інтеграла до обчислення інтеграла . Знаючи інтеграл , можемо послідовно, для прикладу, знайти інтеграли , не виконуючи самої операції інтегрування

,

.

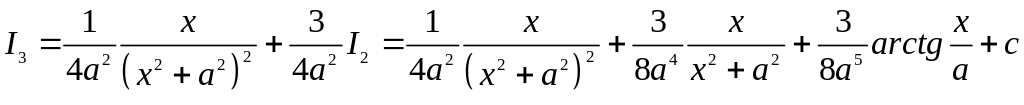На завершення розгляду методу інтегрування частинами отримаємо інтег–рал 22 з таблиці Б.

.

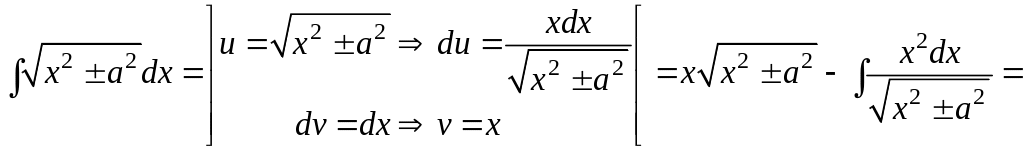
Ми отримали, що . Звідси

.

1.3. Інтегрування деяких класів функцій