12. Перелічити основні передумови регресійного аналізу. Сформулювати ідею принципу максимальної правдоподібності і показати, що по цьому принципу найкращими оцінками параметрів моделі є мнк–оцінки.

Предпосылки регрессионного анализа: 1) y(x_i) = y_p(x_i) + e_i (все ошибки относятся только к результативному признаку у, объясняющие переменные х измерены без ошибок); 2) М(e_i) = 0 – систематических ошибок нет, выбранная модель адекватная; 3) М(е_ie_j) = 0 – ошибки разных наблюдений не коррелированы (наблюдения независимые); 4) – наблюдения равноточные; 4) ошибки распределены нормально. Отсюда получаем плотность распределения отдельных ошибок и плот­ность распределения системы независимых ошибок . Согласно “принципу максимума правдоподобия” параметры модели (и оценку дисперсии _e²) надо выбрать так, чтобы получить максимум функции распределения f (наблюдаемая система ошибок e_i должна быть наиболее вероятной). Из условий максимума плотности совместного распределения следуют метод наименьших квадратов (параметры модели необходимо определять из условий минимума e²), а оценка дисперсии случайной ошибки оказывается равной .

13. Викласти ідею розрахунку дисперсій коефіцієнтів регресії і дисперсій розрахункових значень. Описати графічний спосіб побудови 95%-вої довірчої смуги на лінію регресії.

Согласно предпосылкам регрессионного анализа, все объясняющие переменные х считаются измеренными точно, все случайные ошибки относятся только к результативному признаку у. Эти ошибки независимые, равноточные (имеют одинаковую дисперсию для любых наблюдений), систематических ошибок нет (т.е. М(e_i) = 0). МНК-оценки коэффициентов регрессии являются линейными комбинациями значений результативного признака у_i с неслучайными коэффициентами, отсюда можно получить выражение ошибки коэффициента регрессии как комбинацию ошибок наблюдений и вычислить ее дисперсию (дисперсия суммы независимых величин равна сумме дисперсий, неслучайные множители возводятся в квадрат). Так, для линейной однофакторной модели коэффициент регрессии вычисляется по формуле , откуда получаем выражение случайной ошибки коэффициента регрессии в виде , где х и s_x – не случайные. Дисперсия этой ошибки равна . Теперь рассмотрим случайную дисперсию расчетных значений как линейную комбинацию случайных величин и b₁  с известными дисперсиями: . Как функция х это есть уравнение сопряженной гиперболы , сдвинутой вправо на величину с полуосями а = s_x и . Достаточно построить только каркас доверительной полосы на линию регрессии. На интервале ширина доверительной полосы практически постоянна и равна удвоенной ошибке среднего ; строим на линии регрессии этот параллелограмм; далее доверительная полоса расширяется, приближаясь к продолжениям диагоналей построенного параллелограмма.

В заключение приведем подробный вывод формулы для дисперсии коэффициента регрессии:

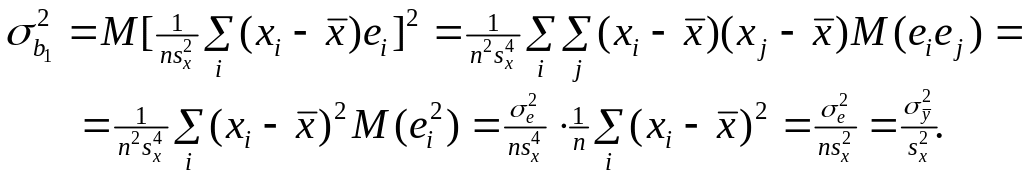
14. Пояснити спосіб вибіру форми зв’язку. Продемонструвати можливості узагальненої лінійної моделі, нелінійної щодо аргументів, але лінійної щодо параметрів. Розглянути стандартні перетворення змінних (логарифмування і перехід до зворотних величин).

Для МНК важно, чтобы форма связи была линейной относительно параметров (а не относительно х), тогда система нормальных уравнений для определения параметров будет линейной. Общий вид двухпараметрических моделей, линейных относительно параметров: Y = a + b X . где Y = F(x, y); X = Ф(х, у). Если эмпирические точки в преобразованных координатах (X, Y) не группируются вокруг некоторой прямой, то принятая форма связи должна быть отвергнута (надо подбирать другую, более подходящую). Чаще всего применяется или логарифмирование переменных, или переход к обратным величинам, что дает дополнительно 7 нелинейных моделей, приведенных в таблице ниже (g² – весовая функция):

Двухпараметрические зависимости Y(y) = a + b X(x)

Преобразования	X = x	X = ln x	X = 1/x
Y = y	Линейная y = a + b x	Логарифмическая y = a + b ln x	Гиперболическая1 y = a + b / x
Y = ln y g2 = y2	Показательная ln y = a + b x y = A eb x	Степенная ln y = a + b ln x y = A xb	S-образная ln y = a + b / x y = A eb / x
Y = 1/y g2 = y4	Гиперболическая 2 1 / y = a + b x		Гиперболическая 3 1 / y = a + b / x

15. Роз’яснити ідею методу зважених найменших квадратів. Показати, що функціональні перетворення результативної ознаки приводять до порушення рівноточности (гомоскедастичністі) спостережень, і запропонувати вагову функцію для усунення наслідків порушення зазначеної передумови регресійного аналізу.

В регрессионном анализе предполагается, что дисперсия остатков модели e_i постоянна, не зависит ни от х, ни от у, ни от номера наблюдения (это свойство называется гомоскедастичностью). При нарушении этой предпосылки (гетероскедастичность) оценки коэффициентов регрессии оказываются смещенными (сдвинутыми). Иногда известен закон изменения дисперсии остатков модели и мы можем подобрать такую функцию g(x, y), при умножении на которую ошибки _i = g_i e_i  становятся гомоскедастичными. Умножим на эту функцию все уравнение регрессии y = b₀ + b₁ x + e и получим модель gy = b₀ g+ b₁ gx +  . Ошибки модели должны быть ортогональны к каждому члену модели, откуда получаем такую систему нормальных уравнений: g²y = b₀ g²+ b₁ g²x  и g²yх = b₀ g²х+ b₁ g²x² . Здесь в отличие от обычных уравнений нормальной системы в каждой сумме присутствует «весовой» множитель g². Решение данной системы формально будет похоже на решение обычной системы, если всюду вместо обычных средних использовать «взвешенные» средние: . Весовая функция g² придает большие «веса» надежным наблюдениям, и меньшие – малонадежным (с большой дисперсией), тем самым компенсирует нежелательные последствия гетероскедастичности. Функциональные преобразования результативного признака Y = F(y) часто приводит к гетероскедастичности (если исходные данные были гомоскедастичными). Действительно, пусть F(у) – желаемое функциональное преобразование, после которого модель становится линейной относительно параметров: F(y_p) = b₀ + b₁ X ; однако F(y_p) = F(y ‑ e)  F(y) – eF '(y), т.е. мы получили модель Y = b₀ + b₁ X +  , где . Если е_i были гомоскедастичными, то после умножения их на гомоскедастичность будет нарушена. Для нейтрализации гетероскедастичности надо всю модель умножить на , т.е. в расчетах следует учесть весовую функцию . Например, при весовая функция будет равна g² = y⁴ .

21