Лабораторные работы №№ 6 – 8 Анализ корреляционных связей. Цель работы.

1. По данным наблюдений двух показателей предлагается определить тип корреляционной связи и выявить возможные выбросы – аномальные наблюдения, явно не относящиеся к данной совокупности (чаще всего выбросы появляются как ошибки в записи чисел). Для этого прежде всего надо построить график разброса точек в осях (Х, У). В докомпьютеную эпоху строили корреляционное поле, группируя данные на ряд интервалов по каждой переменной. Несмотря на наличие компьютера, мы в обязательном порядке будем строить корреляционное поле, т.к. оно нам понадобится для изучения некоторых других проблем анализа связей.

2. Независимо от расположения экспериментальных точек предлагается найти МНК-оценки параметров линейной зависимости, построить ее график , оценить тесноту линейной связи и ее значимость. Для сравнения параметры линейной зависимости (коэффициенты регрессии) следует найти по исходным данным и по сгруппированным (более того, для дальнейшей работы нам понадобятся расчеты именно по сгруппированным данным).

3. Т.к. у нас имеется корреляционное поле, можно построить "эмпирическую линию регрессии" – кусочно-линейный график с узлами (Х_i ,U_i ), где – средние интервальные (средние значения результатив­ной переменной в каждой группе по Х_i ). С помощью дисперсионного анализа проверяется значимость существующей корреляционной связи (не налагая никаких предположений о ее типе). Вычисляется более объективная оценка тесноты существующей связи – корреляционное отношение вместо коэффициента корреляции). Для ординат узлов эмпирической линии регрессии полезно вычислить интервальные оценки (доверительные интервалы).

4. Проверяем адекватность линейной модели, сравнивая корреляцион­ное отношение с коэффициентом корреляции (по готовой формуле или заполняя соответствующую таблицу дисперсионного анализа).

5. Когда неизвестно направление причинно-следственных связей, рассчитывают параметры "сопряженной модели", где в качестве результатив­ной принимается переменная Х, или "диагональная регрессия" Фриша, когда обе переменные являются разными следствиями одной и той же причины.

6. Корреляционное поле можно рассматривать как таблицу сопряжен­ности категорий двух качественных показателей. Появляется возможность оценить значимость существующей связи по критерию Пирсона, а тесноту связи – по коэфициенам контингенции. Полезно сравнить результаты оценок тесноты связи и ее значимости по разным методикам.

Исходные данные
№	Х	У	№Х	№У	Шифр
1	1,182	52	8	1	801
2	1,076	70	7	2	702
3	0,999	60	6	1	601
4	0,646	95	3	5	305
5	0,740	97	4	5	405
6	0,646	95	3	5	305
7	0,740	97	4	5	405
8	0,920	68	6	2	602
9	1,063	65	7	2	702
10	1,076	65	7	2	702
11	1,024	60	7	1	701
12	1,063	65	7	2	702
13	0,646	90	3	4	304
14	0,733	75	4	3	403
15	0,74	92	4	5	405
16	0,826	75	5	3	503
17	1,063	65	7	2	702
18	1,076	65	7	2	702
19	0,999	67	6	2	602
20	0,931	67	6	2	602
21	0,495	132	1	9	109
22	1,329	100	10	5	1005
23	0,835	72	5	3	503
24	1,166	58	8	1	801
25	1,135	60	8	1	801
26	0,931	67	6	2	602
27	1,076	65	7	2	702
28	1,024	62	7	2	702
29	0,999	68	6	2	602
30	0,835	75	5	3	503
31	0,826	75	5	3	503
32	0,740	100	4	5	405
33	0,733	74	4	3	403
34	0,495	116	1	7	107
35	0,585	120	2	7	207
36	0,999	68	6	2	602
37	0,999	68	6	2	602
38	0,733	88	4	4	404
39	0,835	75	5	3	503
40	0,826	70	5	2	502
41	0,999	67	6	2	602
42	0,999	67	6	2	602
43	0,999	67	6	2	602
44	0,594	96	2	5	205

Представление данных.

Исходные данные обычно записыва­ются в виде таблицы из двух столбцов Х, У; можно также добавить столбец номеров наблюдений №. Такое расположение удобно для расчетов, но не удобно для отчета, если длинный столбец данных не помещается на одной странице. Имеется возможность компактно расположить данные в несколько столбцов, но тогда появляются несмежные диапазоны знчений переменных. В формулах адреса несмежных диапазонов надо указывать мышкой при нажатой клавише Ctrl. Можно любому диапазону присвоить краткое имя и использовать его в формулах.

На компьютере имеется возможность посмотреть на график разброса точек (х, у):

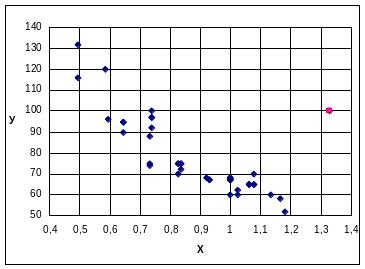
Из этого графика визуально определя­ем наличие выброса (точка № 22 – выделена красным цветов на графике и в таблице). Выбросы, естественно, надо удалять.

При отсутствии компьютера данные следует сгруппировать и отобразить их на, так называемом, корреляционном поле. Нам все-равно понадобятся сгруппированные данные для изучения некоторых проблем анализа связей, поэтому переходим к рассмотрению метода двойной группировки данных.