Задача 11

Исследовать на экстремум функционал , , .

РЕШЕНИЕ

Для того чтобы функционал вида при достигал экстремума на множестве функций, удовлетворяющих условиям , необходимо, чтобы функция удовлетворяла уравнению Эйлера .

В данном случае , а уравнение Эйлера примет вид , тогда , то есть . Понижая степень этого уравнения с помощью замены , получаем , тогда , следовательно , откуда . Учитывая граничные условия, для нахождения постоянных и имеем систему уравнений

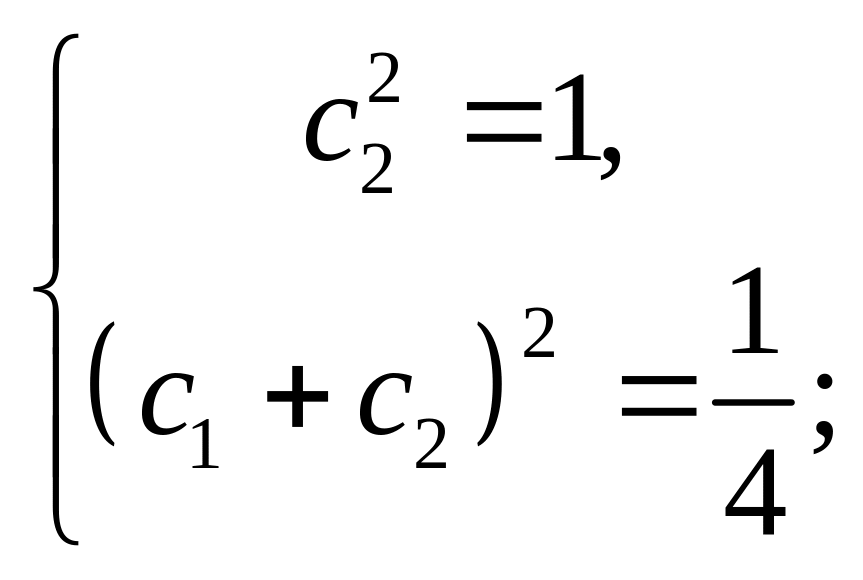
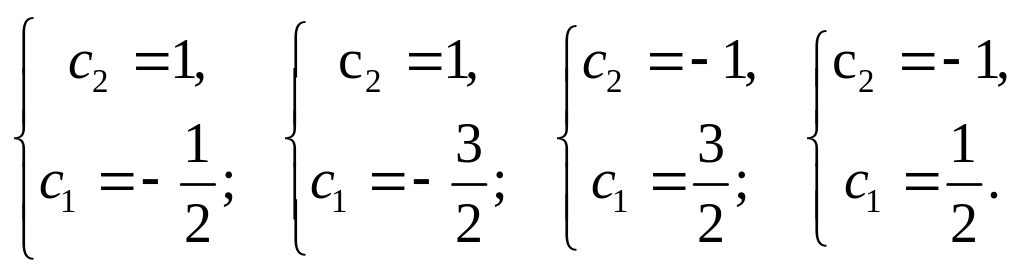
Подставляя найденные значения, убеждаемся, что экстремумами могут быть только параболы и .

Теперь, для того чтобы функционал вида достигал на экстремали минимума (соответственно максимума), необходимо, чтобы вдоль этой кривой выполнялось усиленное условие Лежандра (соответственно ) и на не было бы точек, сопряженных с точкой , то есть уравнение Якоби с начальными условиями имело бы не нулевое решение , где , а .

Поэтому рассмотрим решения соответствующих уравнений Якоби. Так как , а , то уравнения Якоби принимают вид

, тогда .

Если , то . Это уравнение типа уравнения Эйлера. Поэтому его решения ищем в виде . Тогда для определения имеем уравнение . Откуда и общее решение .

Учитывая начальные условия , получаем . Заметим, что эта функция обращается в нуль при . Следовательно, экстремаль не удовлетворяет одному из условий экстремума. Поэтому дальнейшим исследованиям подлежит только экстремаль . Для нее уравнения Якоби с начальными условиями имеет решение , не обращающееся в нуль на . При этом выполняется усиленное условие Лежандра .

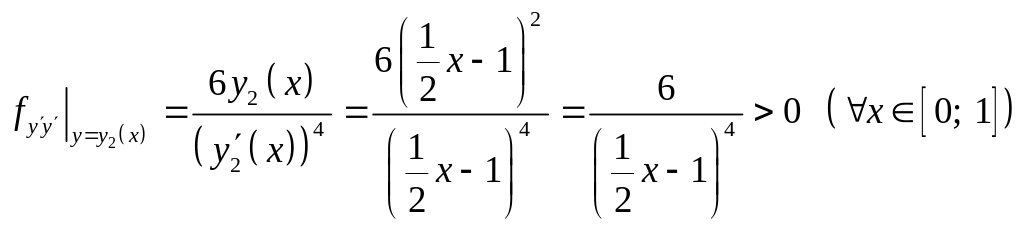Следовательно, на экстремали данный функционал достигает минимума.

Задача 12

Интегрируема ли по Риману функция

на отрезке ? Интегрируема ли она по Лебегу на относительно меры Лебега ? Если интегрируема по Лебегу, то найти ее интеграл.

РЕШЕНИЕ

Докажем, что функция не является интегрируемой по Риману на . Для этого рассмотрим произвольное разбиение отрезка и пусть . В качестве отмеченных точек вначале рассмотрим рациональные точки. Тогда соответствующая интегральная сумма функции равна . Эту интегральную сумму можно считать интегральной суммой для непрерывной функции , и поэтому .

Если же в качестве отмеченных точек взять иррациональные точки, то соответствующая интегральная сумма функции равна . Полученную интегральную сумму также интерпретируем как интегральную сумму непрерывной функции , и поэтому .

Таким образом, предел интегральных сумм зависит от выбора отмеченных точек. Следовательно, не является интегрируемой по Риману.

Рассматриваемая функция всюду (относительно меры Лебега ) совпадает на с непрерывной функцией , и поэтому измерима. Кроме того, функция ограничена. Тогда интегрируема по Лебегу на .

Используя эквивалентность функций и на отрезке и то, что интегралы Римана и Лебега равны (для интегрируемой по Риману функции), имеем .