Задача 2

Доказать, что пространство непрерывных на функций с метрикой является полным.

РЕШЕНИЕ

Метрическое пространство с метрикой является полным, если любая его фундаментальная последовательность сходится в нем. Рассмотрим фундаментальную последовательность непрерывных на функций. Следовательно,

Зафиксировав , получим числовую последовательность , обладающую свойством:

,

т.е. . По достаточному признаку Коши сходимости числовой последовательности, следует, что . Обозначим его .

Таким образом, . Вернемся к неравенству (2.1.1) и перейдем в нем к пределу при . Получим, что . Откуда следует, что у функциональной последовательности существует предел, равный . Осталось показать, что .

Рассмотрим:

В силу сходимости функциональной последовательности , по метрике , следует, что при достаточно большом значении , и . Поэтому,

. Теперь, в силу непрерывности функции , следует, что .

Итак,

,

что и доказывает непрерывность функции .

Задача 3

Показать, что отображение , где является сжимающим и найти его неподвижную точку.

РЕШЕНИЕ

Отображение из одного метрического пространства в другое является сжимающим (сжатием), если существует такое число , что .

В пространстве непрерывных функций на отрезке метрика задается следующим образом: .

Рассмотрим

Итак, , следовательно, является сжатием. Так как пространство является полным (см. пример 2), по принципу сжимающих отображений у отображения существует неподвижная точка такая, что . Ее можно найти методом последовательных приближений. За начальное приближение возьмем , тогда

,

,

, . . .

, и так далее.

Причем .

Итак, неподвижной точкой отображения является функция .

Задача 4

Пусть , а топология в нем определяется множествами , всевозможными интервалами , где , и любыми их объединениями. Найти предел последовательности .

РЕШЕНИЕ

Точка топологического пространства называется пределом последовательности , если любая ее окрестность содержит все члены данной последовательности, начиная с некоторого номера . Нетрудно видеть, что ни одна точка , , не может быть пределом указанной последовательности, т.к. любая ее окрестность вида содержит конечное число элементов . Рассмотрим точку . Поскольку любое объединение интервалов эту точку не содержит, то в пространстве единственной ее окрестностью является само множество (содержащее все точки последовательности). Следовательно, единственным пределом последовательности в пространстве является точка .

Задача 5

Является ли нормой в пространстве непрерывно дифференцируемых на функций следующая функция ?

РЕШЕНИЕ

Линейное пространство над полем действительных чисел называется нормированным, если каждому элементу поставлено в соответствие неотрицательное число , называемое нормой , так, что выполнимы следующие аксиомы:

1. ;

2. и ;

3. .

Проверим выполнение аксиом. так как модуль любого числа является числом неотрицательным. Если на , то . Обратно, если , то и на . Следовательно, ( =const). Так как , то , т.е на . Таким образом, первая аксиома выполняется. Теперь вторая:

.

Проверим выполнение третьей аксиомы:

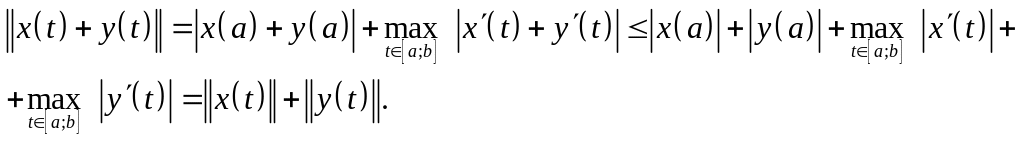
Итак, все три аксиомы выполняются. Следовательно, данная функция является нормой.