Задача 6

Пусть - гильбертово пространство функций, суммируемых с квадратом на , скалярное произведение в котором имеет вид . Для данной функции найти элемент наилучшего приближения элементом подпространства многочленов степени .

РЕШЕНИЕ

Поскольку при заданном в пространстве со скалярным произведением от элемента наименее удалена его -ая частичная сумма ряда Фурье, то искомый многочлен совпадает с многочленом Фурье второй степени функции , т.е. , где - элементы ортонормированной системы в , , - коэффициенты Фурье функции .

Для того, чтобы найти , применим процесс ортогонализации к линейно независимым функциям . Учитывая, что , найдем : . Далее, , где . Так как , то . Кроме того, . Следовательно, . Перейдем теперь к построения функции , где . Так как , а .

Поэтому, . Поскольку , то .

Итак, чтобы построить искомый многочлен, осталось подсчитать коэффициенты Фурье функции :

Тогда

Задача 7

Показать, что оператор является линейным, ограниченным и найти его норму, если

РЕШЕНИЕ

Оператор , действующий из линейного пространства в линейное пространство называется линейным, если .

Рассмотрим

Итак, данный оператор является линейным. Он будет ограниченным, если найдется константа такая, что для всех . Норма в пространстве непрерывных на задается следующим образом: . Поэтому

Таким образом, оператор является ограниченным, а его нормой , по определению, будет наименьшая из таких констант , что для всех . Следовательно, . При этом . Рассмотрим . Поэтому

Итак, . Следовательно .

Задача 8

Определить общий вид решения интегрального уравнения и найти его решение с помощью неопределенных коэффициентов.

РЕШЕНИЕ

Данное интегральное уравнение может быть преобразовано следующим образом: . Следовательно, решения нужно искать в виде , а неизвестные коэффициенты и можно найти путем подстановки его в исходное уравнение:

Откуда получаем систему:

Следовательно, . Тогда решением данного уравнения является функция .

Задача 9

Решить интегральное уравнение 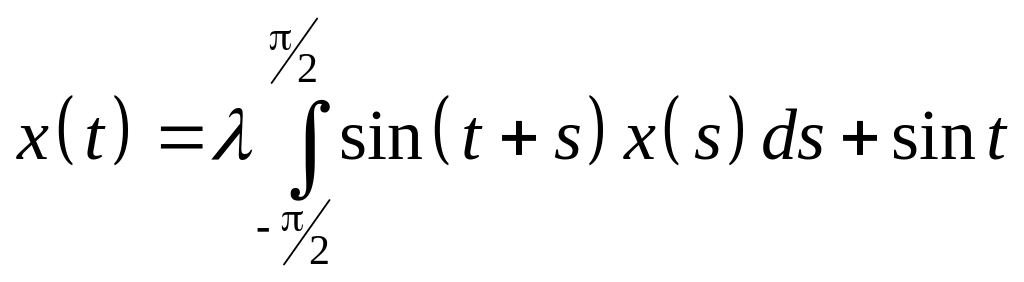с вырожденным ядром.

РЕШЕНИЕ

Решение интегрального уравнения с вырожденным ядром может быть найдено в виде . Коэффициенты определяются из системы линейных уравнений , где .

У данного интегрального уравнения ядро , т.е. , , , . Значения коэффициентов

Для нахождения коэффициентов получили систему

Откуда, при , , , а при система не имеет решений. Следовательно, данное интегральное уравнение с вырожденным ядром имеет решение:

лишь при , а в противном случае решений нет.

Задача 10

Построить резольвенту интегрального уравнения и с ее помощью найти решение.

РЕШЕНИЕ

Для того, чтобы построить резольвенту интегрального уравнения , необходимо сначала построить последовательность итерированных ядер:

, .

Для данного уравнения

, ,

,

(последнее можно доказать методом математической индукции). После чего резольвента может быть найдена по следующей формуле: . В нашем случае резольвента .

Решение уравнения с помощью резольвенты записывается в виде . Следовательно, решением данного уравнения будет функция .