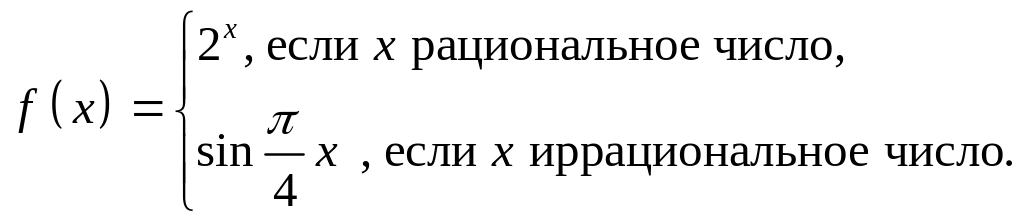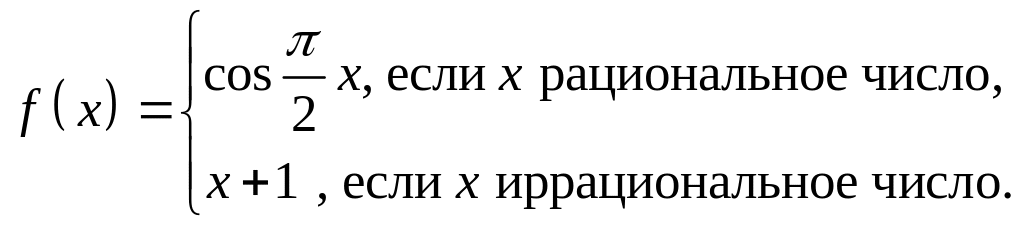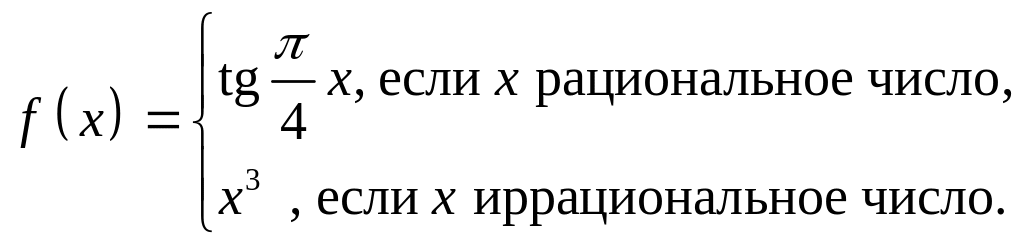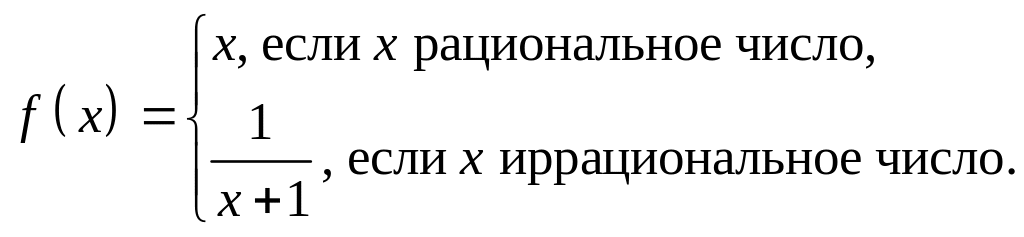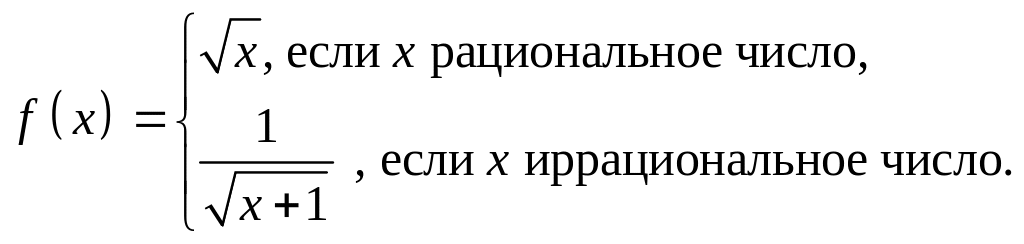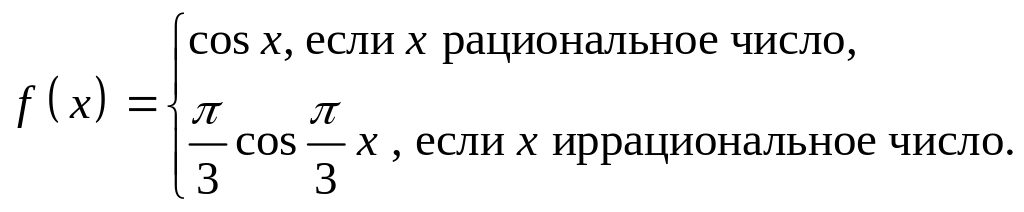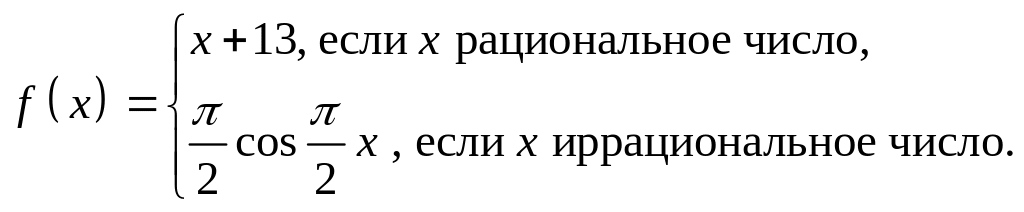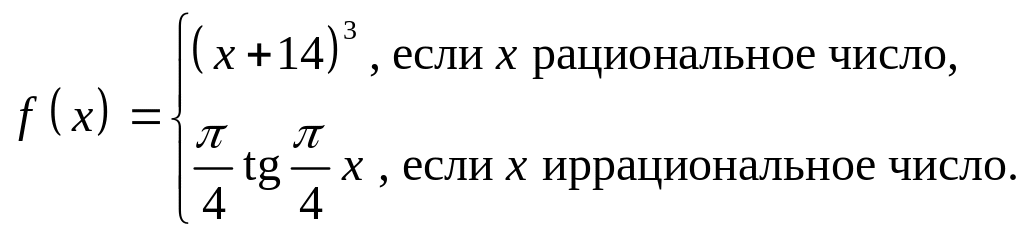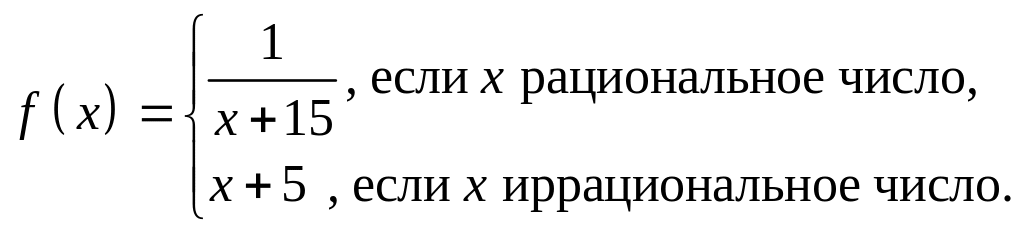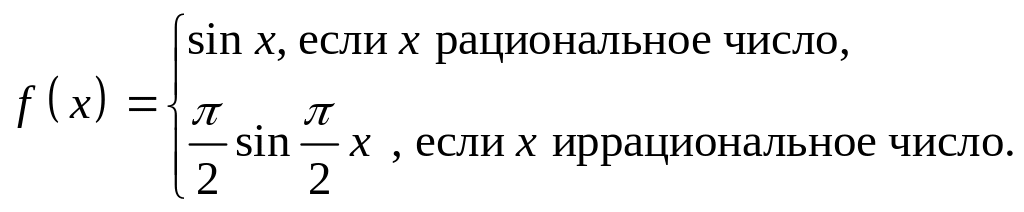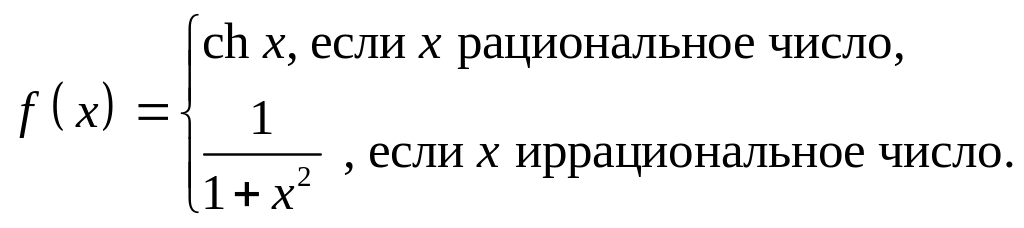- •Задание 1
- •Доказать, что формулой определяется метрика в .
- •Доказать, что формулой определяется метрика в .
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Задача 8
- •Задача 9
- •Задача 10
- •Задача 11
- •Задача 12
- •Библиографический список
- •Сборник индивидуальных заданий по функциональному анализу
- •426069, Г. Ижевск, ул. Студенческая, 7
Задание 5
Можно ли в
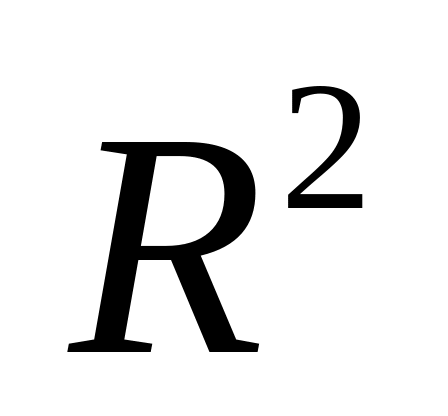 определить норму формулой
определить норму формулой
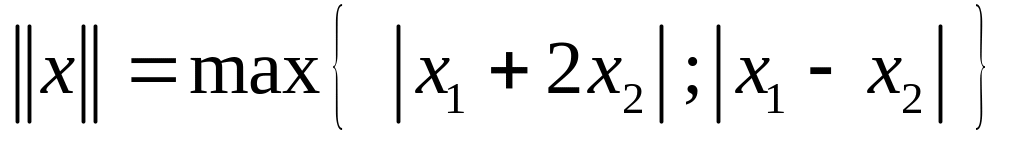 ,
где
,
где
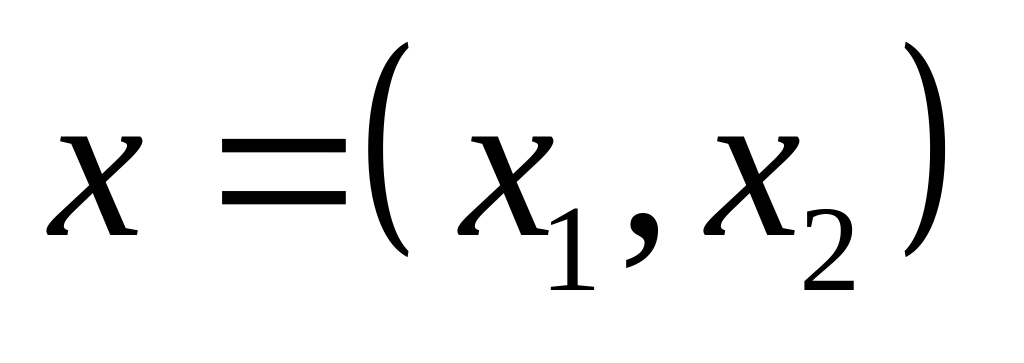 ?
?Можно ли в пространстве непрерывных на функций определить норму следующим образом
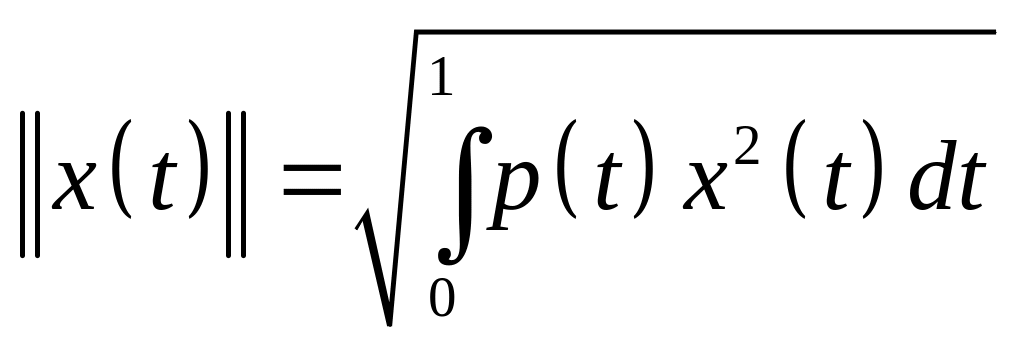 ,
,
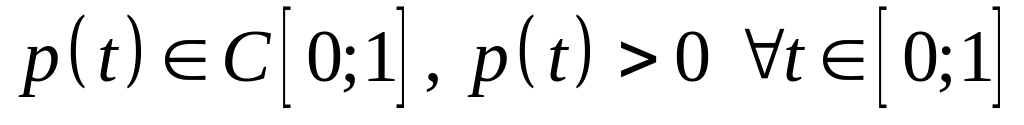 ?
?Можно ли в пространстве непрерывно дифференцируемых на
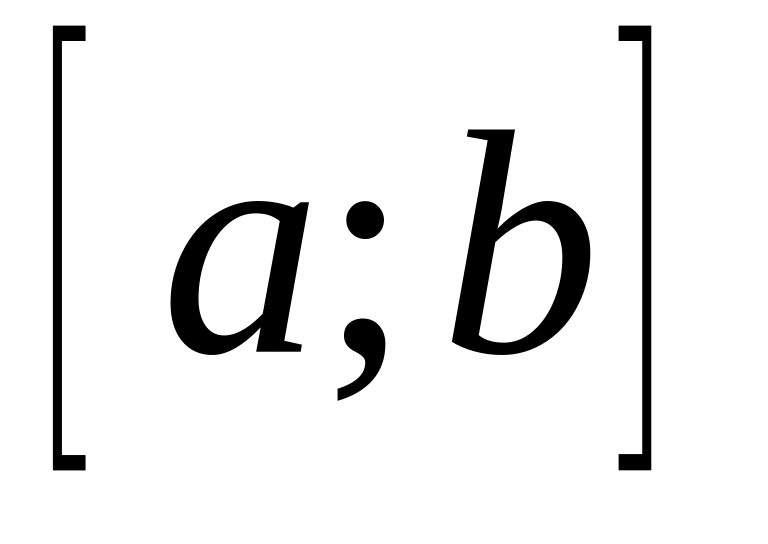 функций определить норму следующим
образом:
функций определить норму следующим
образом:
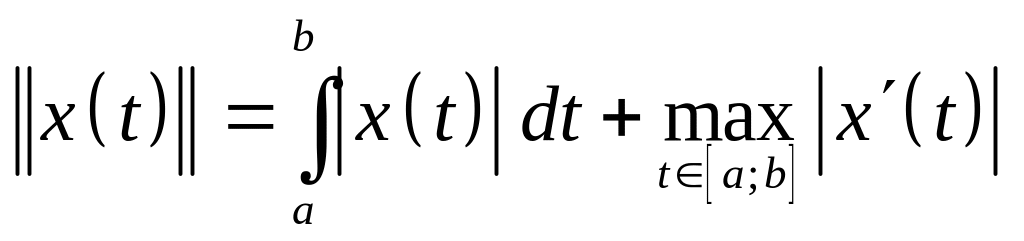 ?
?Убедитесь, что для пространства выполняются аксиомы нормы, если
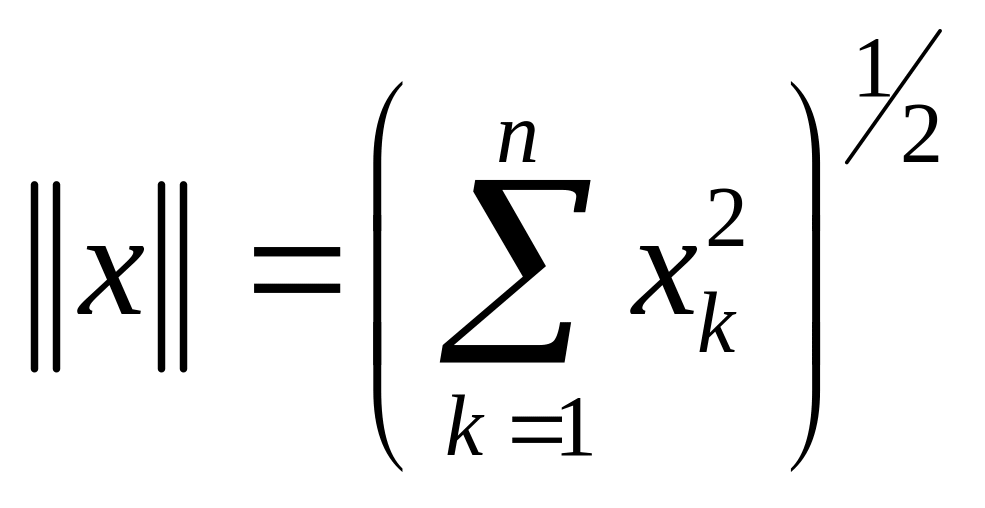 .
.Убедитесь, что для пространства выполняются аксиомы нормы, если
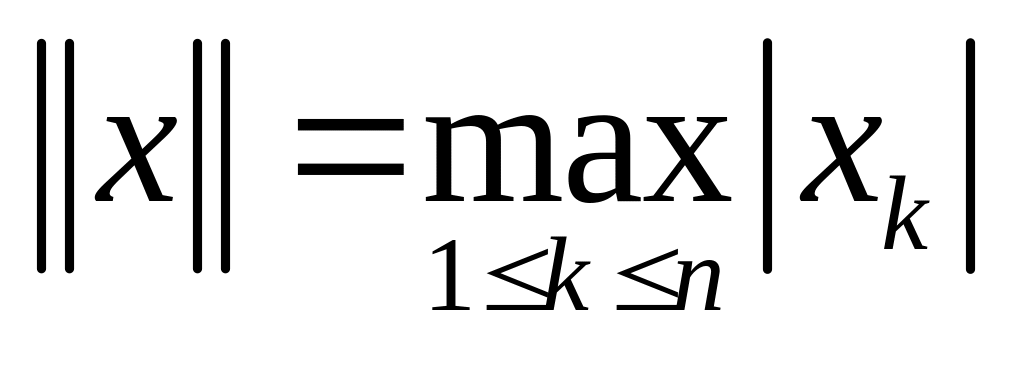 .
.Убедитесь, что для пространства выполняются аксиомы нормы, если
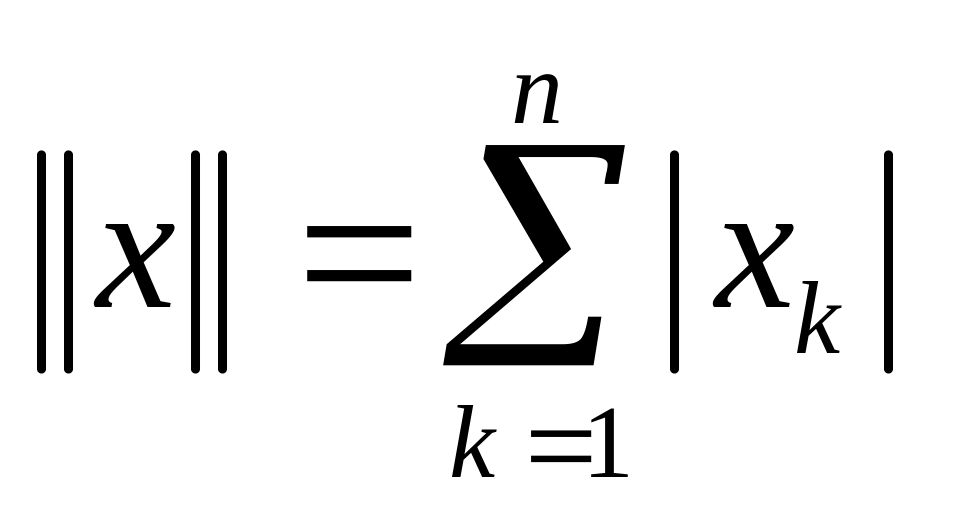 .
.Убедитесь, что в пространстве
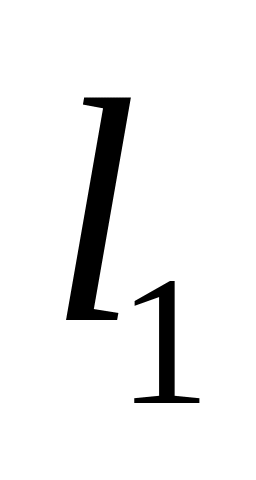 последовательностей
последовательностей
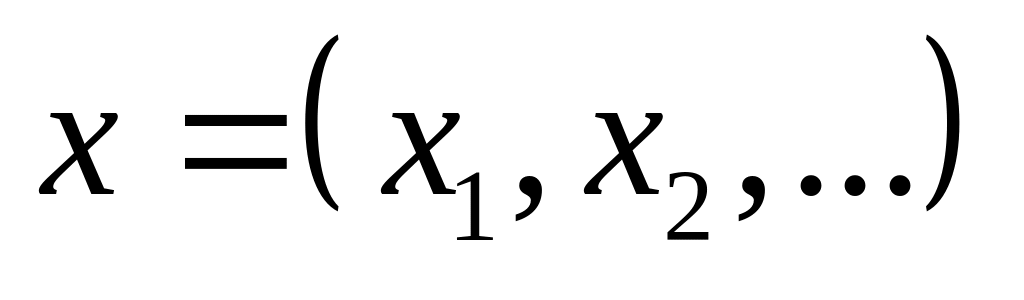 ,
где
,
где
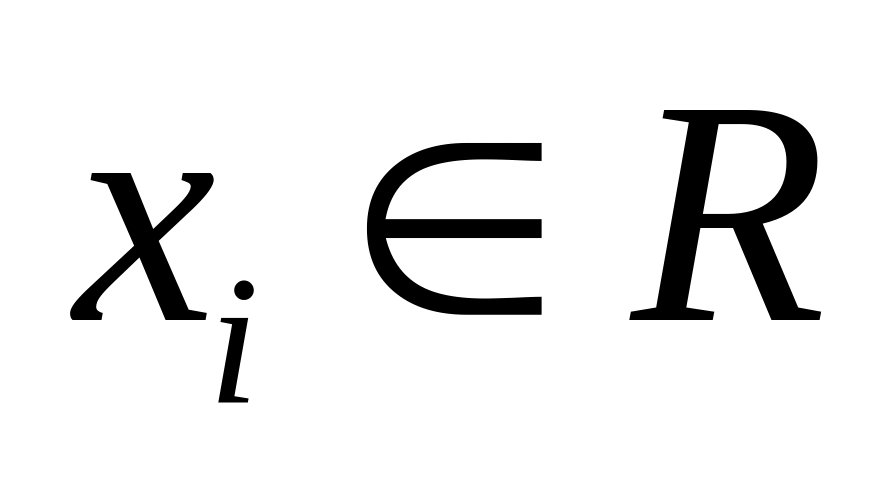 ,
удовлетворяющих условию
,
удовлетворяющих условию
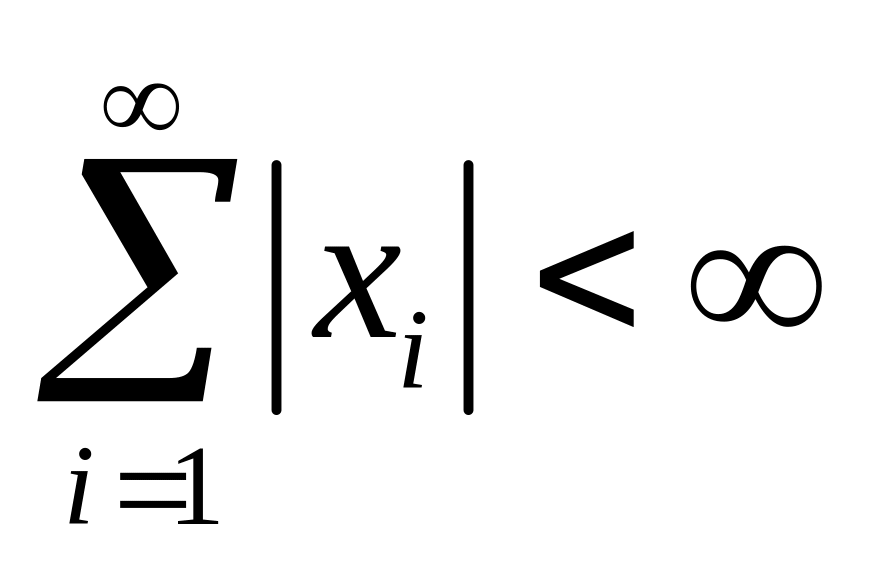 с нормой
с нормой
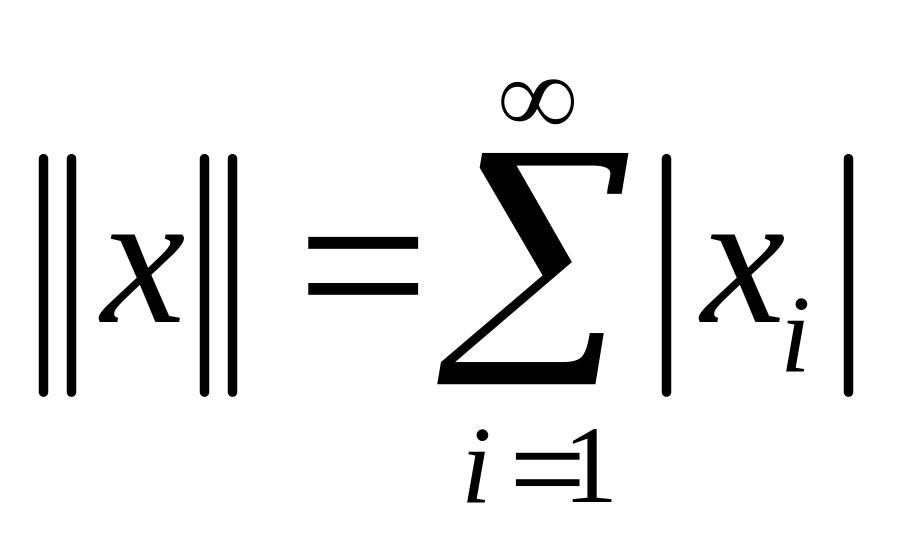 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве последовательностей , где , удовлетворяющих условию
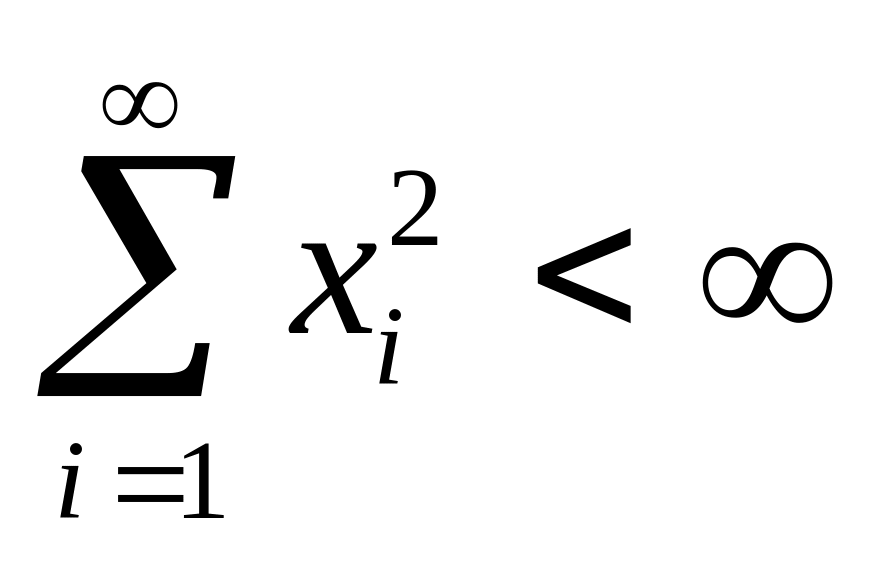 с нормой
с нормой
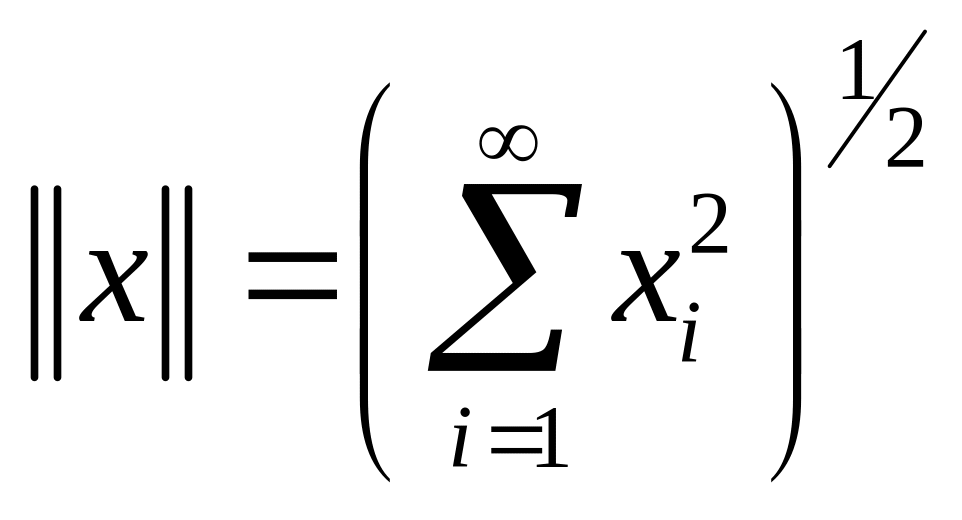 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве ограниченных последовательностей ( ) с нормой
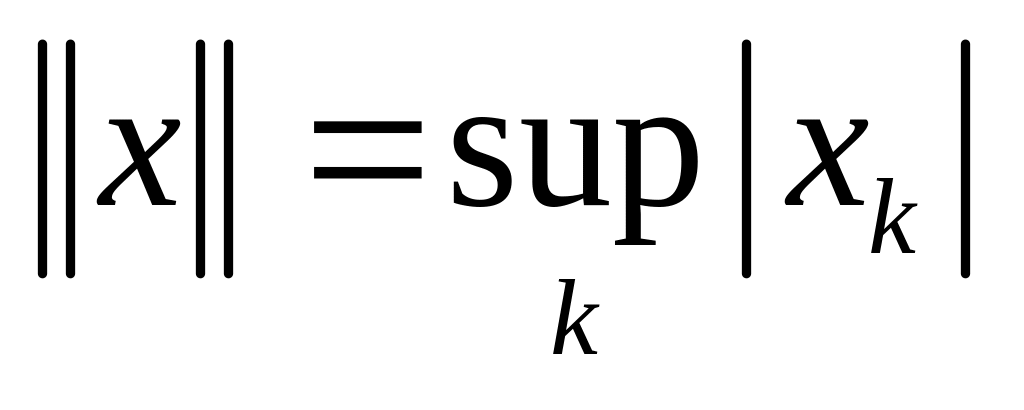 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве
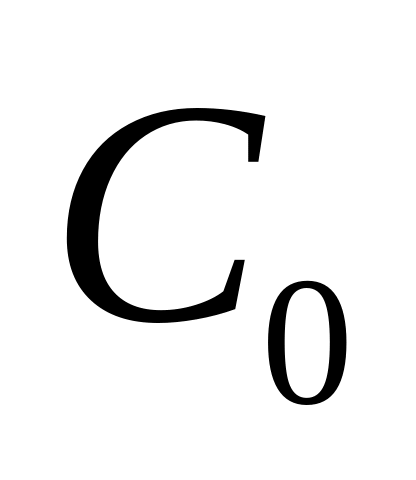 сходящихся к нулю последовательностей
(
)
с нормой
сходящихся к нулю последовательностей
(
)
с нормой
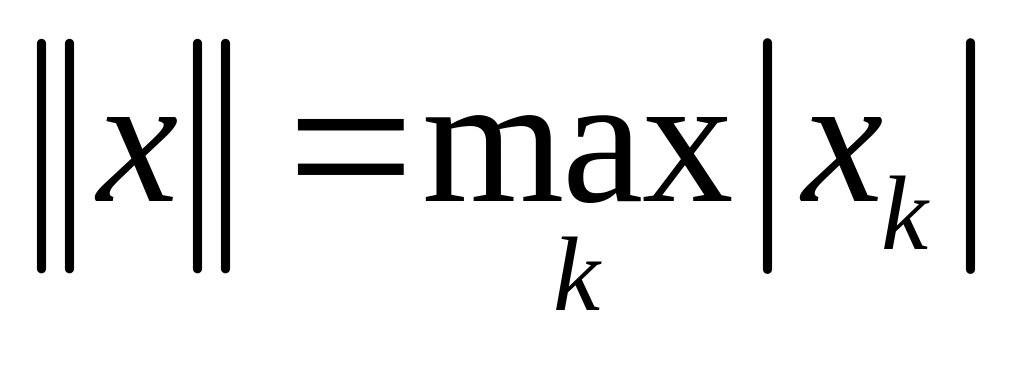 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве сходящихся последовательностей (
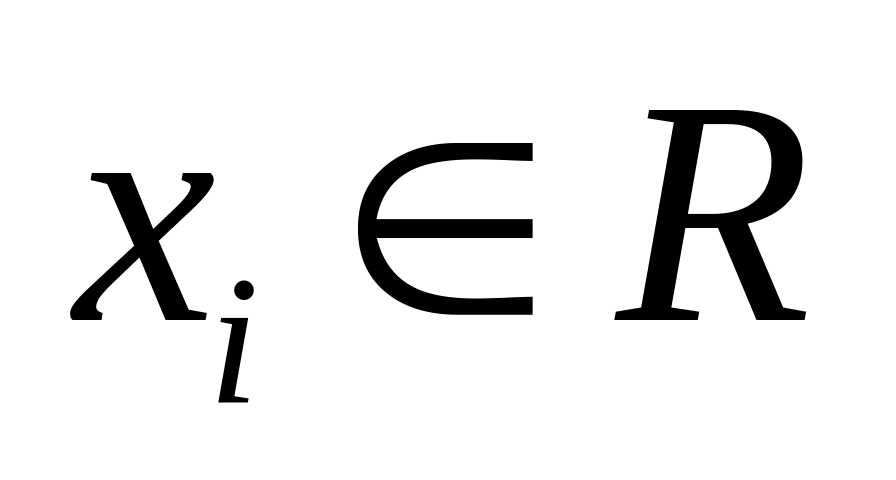 )
с нормой
)
с нормой
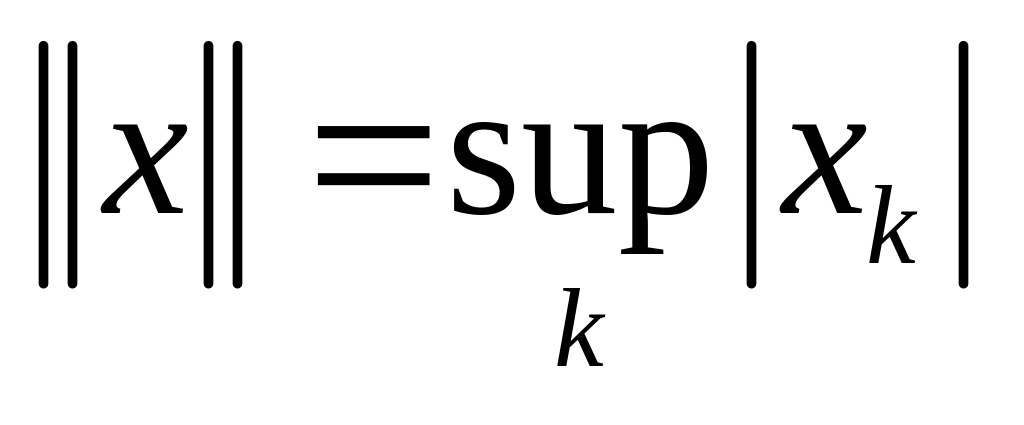 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве
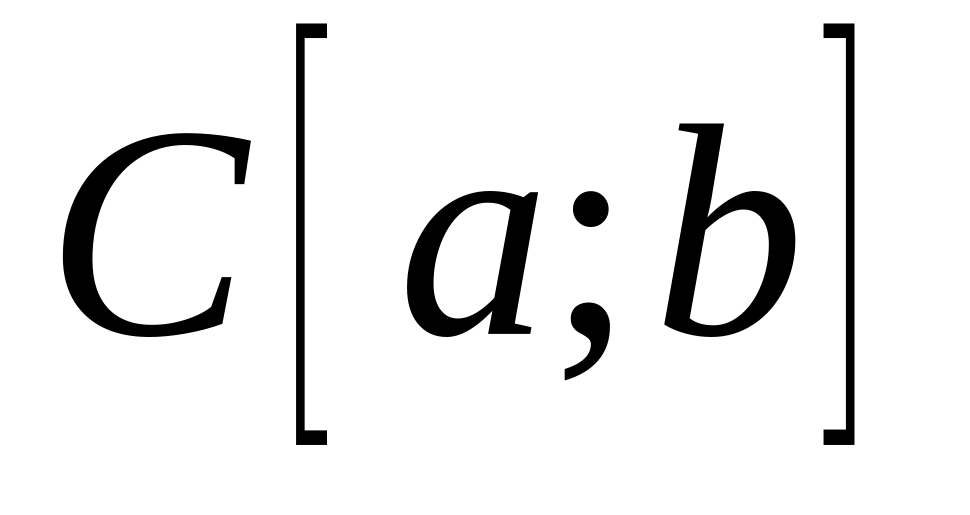 непрерывных на
непрерывных на
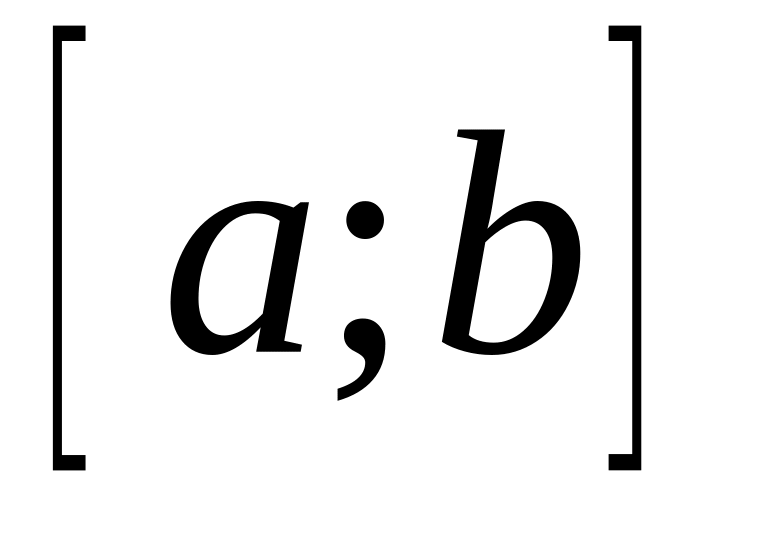 функций с нормой
функций с нормой
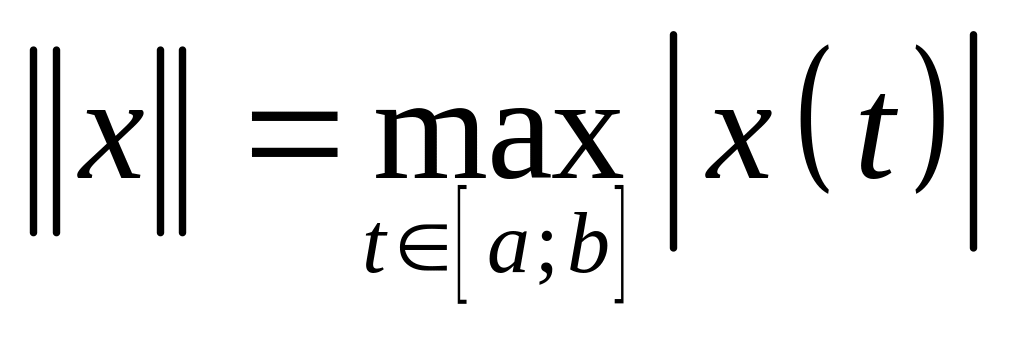 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве
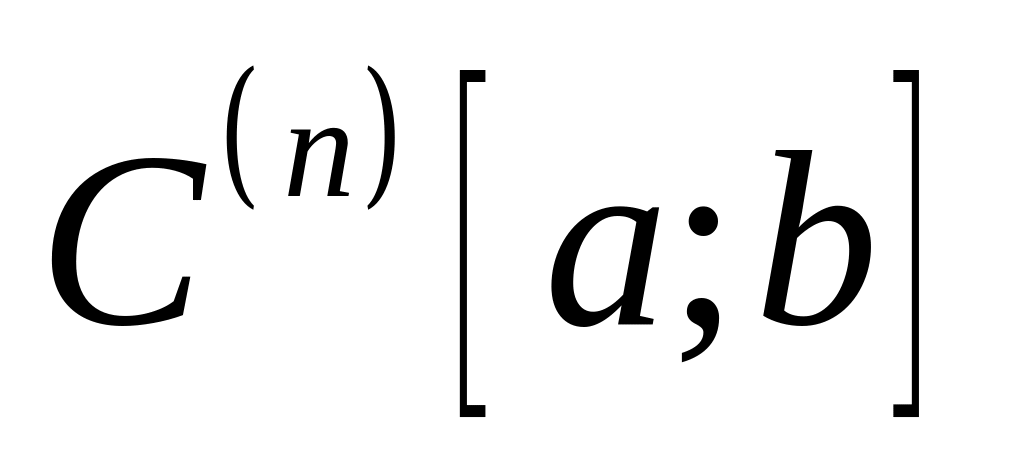 раз непрерывно дифференцируемых на
функций с нормой
раз непрерывно дифференцируемых на
функций с нормой
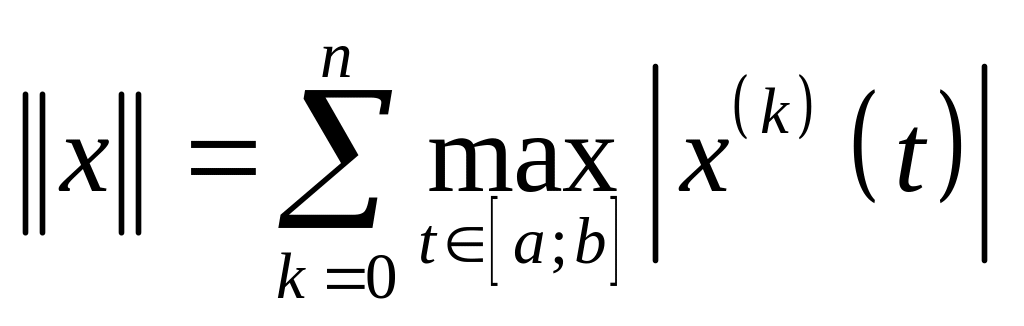 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве
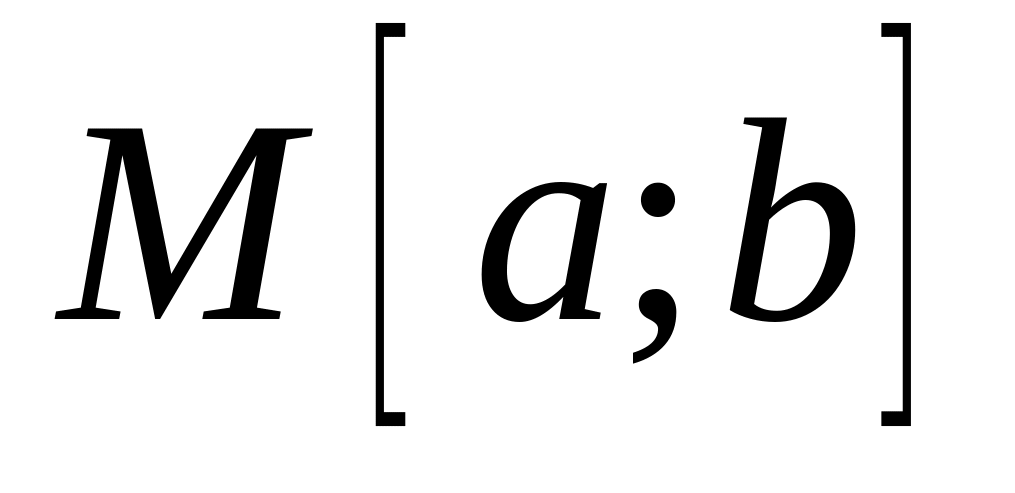 всех ограниченных на
функций с нормой
всех ограниченных на
функций с нормой
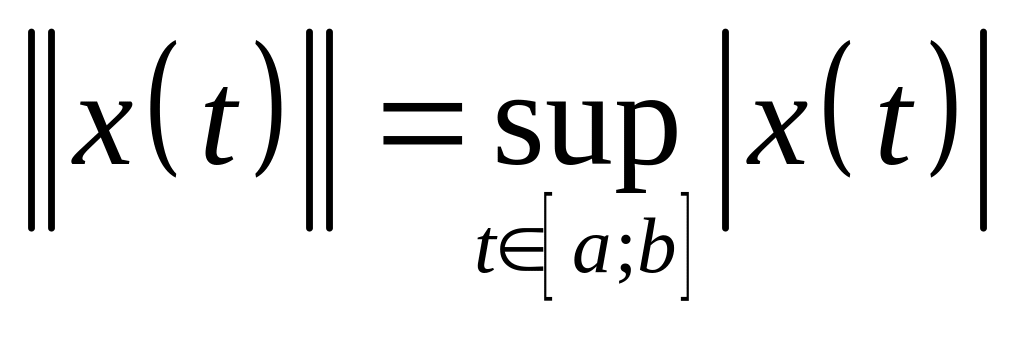 выполняются аксиомы нормы.
выполняются аксиомы нормы.Пусть
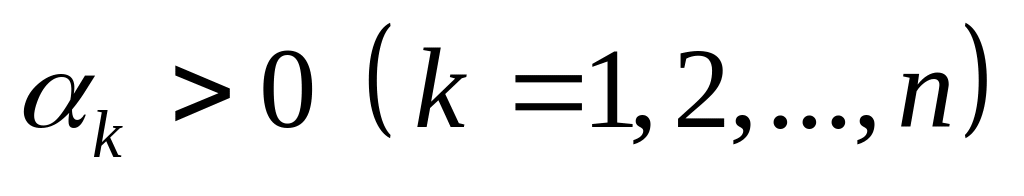 .
Доказать, что в пространстве
можно ввести норму следующим образом
.
Доказать, что в пространстве
можно ввести норму следующим образом
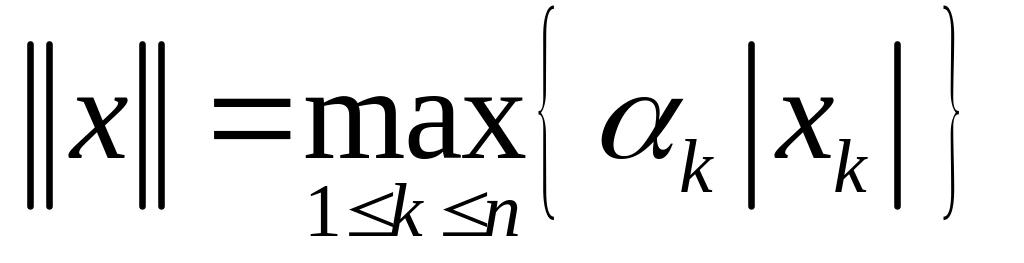 .
.Пусть . Доказать, что в пространстве можно ввести норму следующим образом
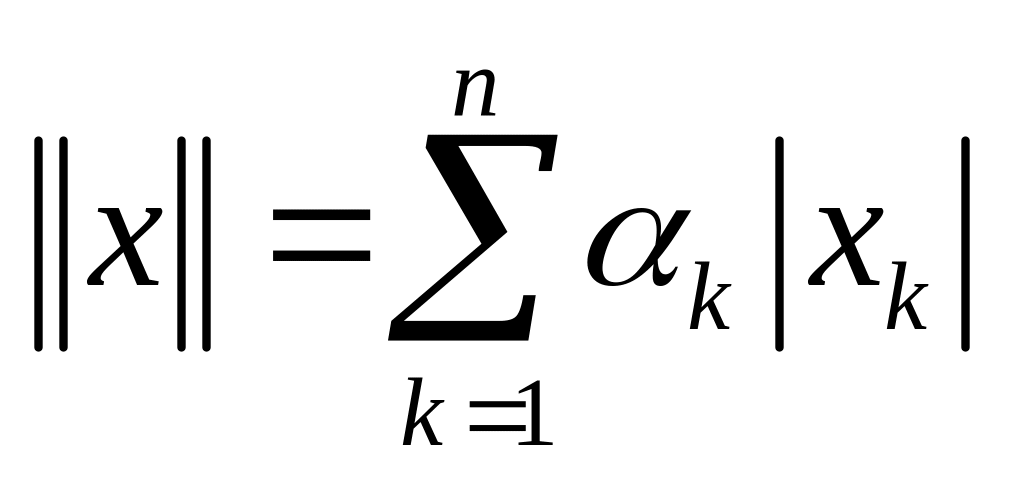 .
.Убедитесь, что в пространстве последовательностей ( ), удовлетворяющих условию
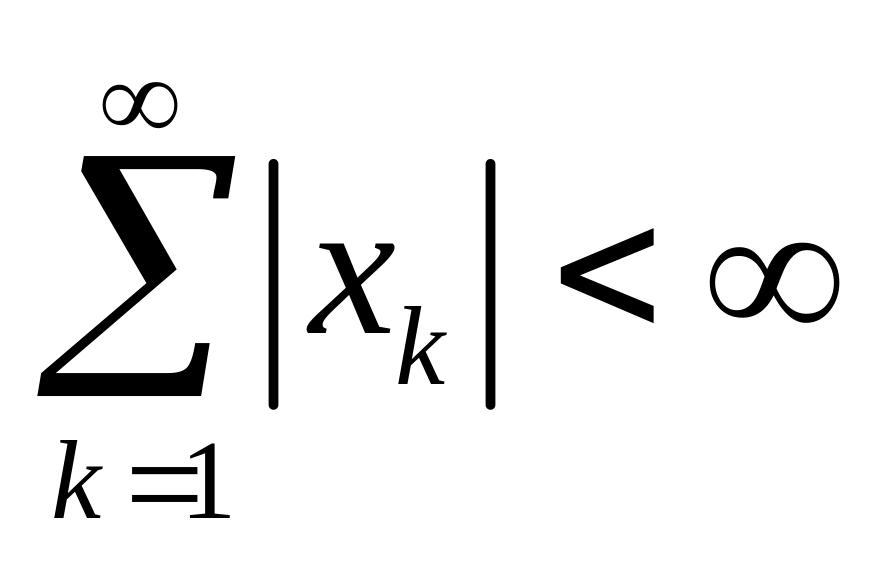 с нормой
с нормой
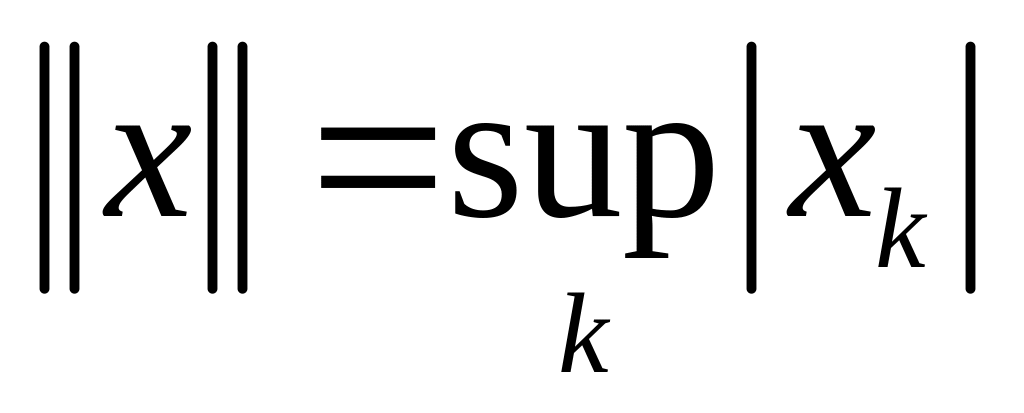 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве
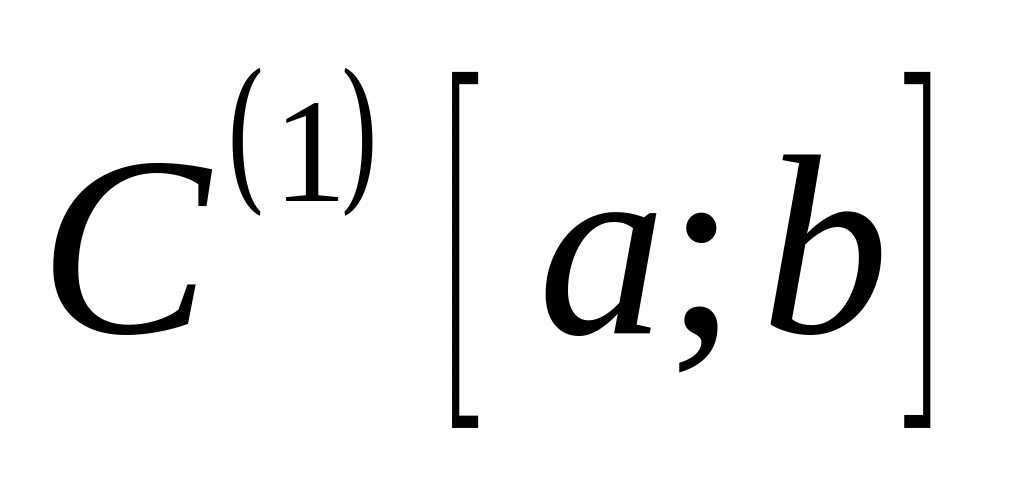 непрерывно дифференцируемых на
непрерывно дифференцируемых на
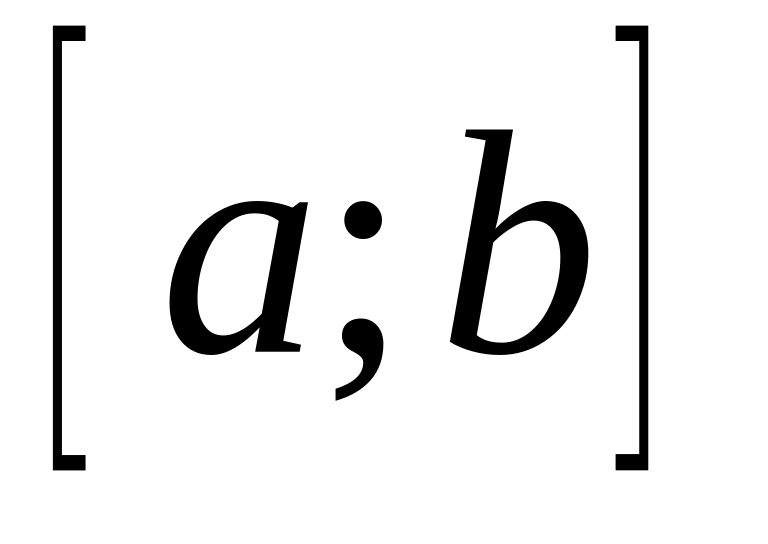 функций с нормой
функций с нормой
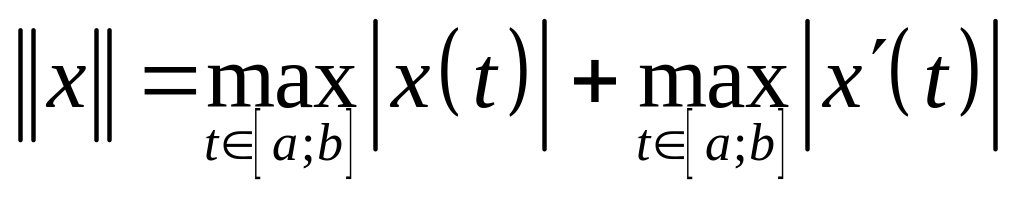 выполняются аксиомы нормы.
выполняются аксиомы нормы.Убедитесь, что в пространстве
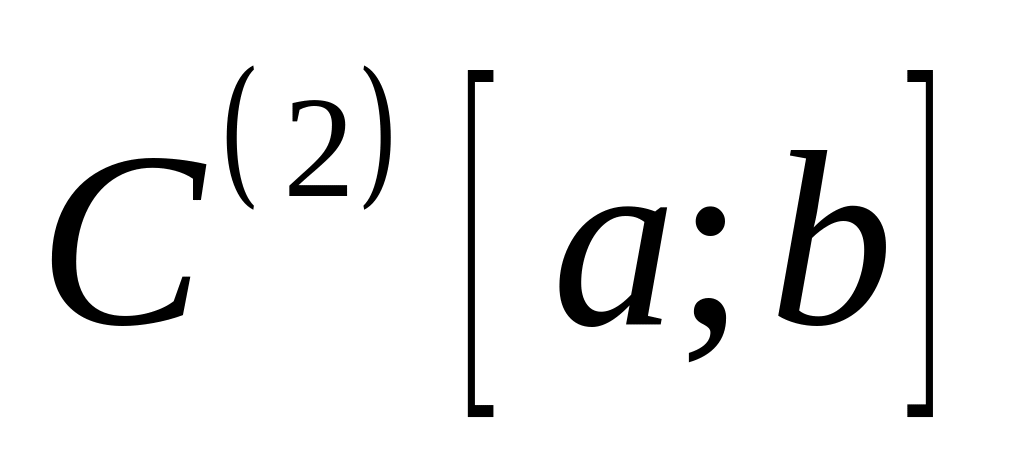 дважды непрерывно дифференцируемых
на
функций с нормой
дважды непрерывно дифференцируемых
на
функций с нормой
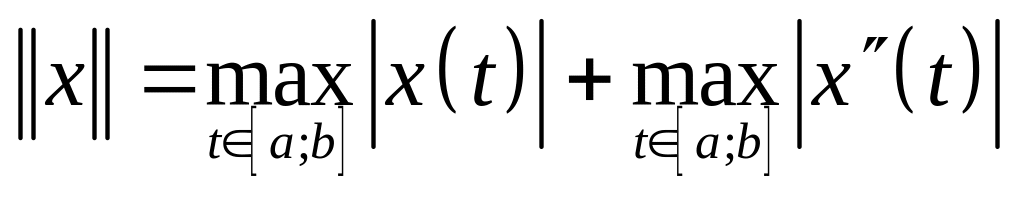 выполняются аксиомы нормы.
выполняются аксиомы нормы.Можно ли в пространстве
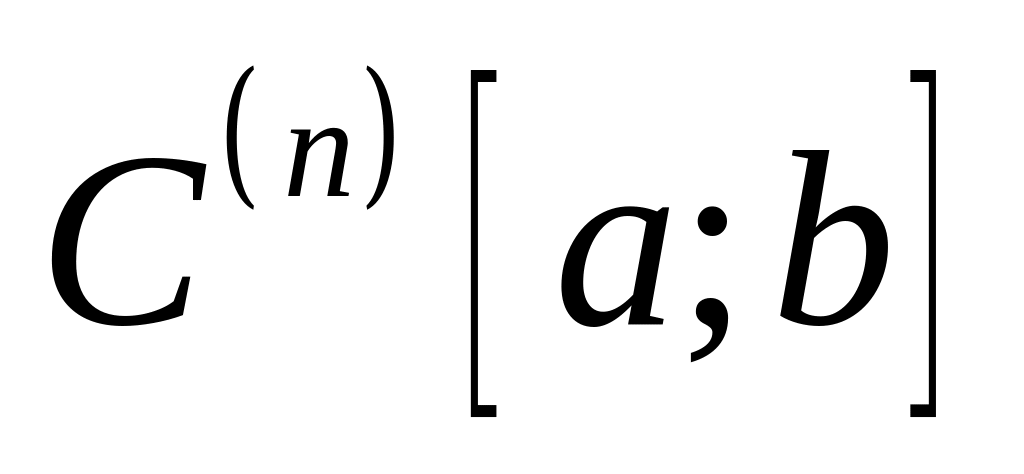 раз непрерывно дифференцируемых на
функций задать норму следующим образом
раз непрерывно дифференцируемых на
функций задать норму следующим образом
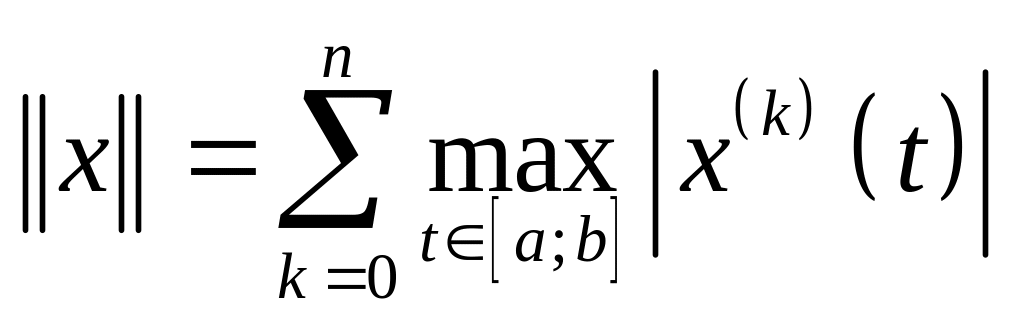 .
.
Задание 6
Пусть
![]() – гильбертово пространство функций
суммируемых с квадратом на
,
скалярное произведение в котором имеет
вид
– гильбертово пространство функций
суммируемых с квадратом на
,
скалярное произведение в котором имеет
вид
![]() .
Для заданной функции
.
Для заданной функции
![]() найти элемент наилучшего приближения
найти элемент наилучшего приближения
![]() элементом подпространства
элементом подпространства
![]() многочленов степени
многочленов степени
![]() .
Построить графики функций
.
Построить графики функций
![]() и
.
и
.
6.1.
|
6.11.
|
6.2.
|
6.12.
|
6.3.
|
6.13.
|
6.4.
|
6.14.
|
6.5.
|
6.15.
|
6.6.
|
6.16.
|
6.7.
|
6.17.
|
6.8.
|
6.18.
|
6.9.
|
6.19.
|
6.10.
|
6.20.
|
ЗАДАНИЕ 7
Доказать, что оператор является линейным ограниченным и найдите его норму, если:
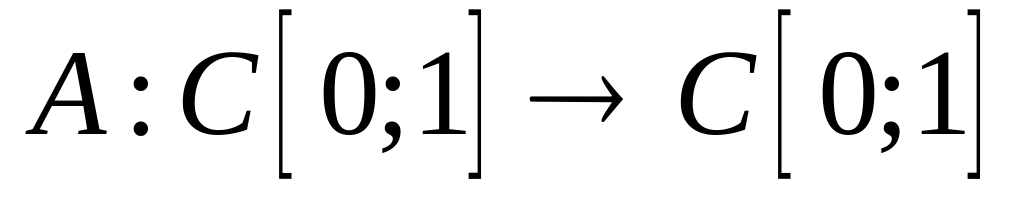 ,
,
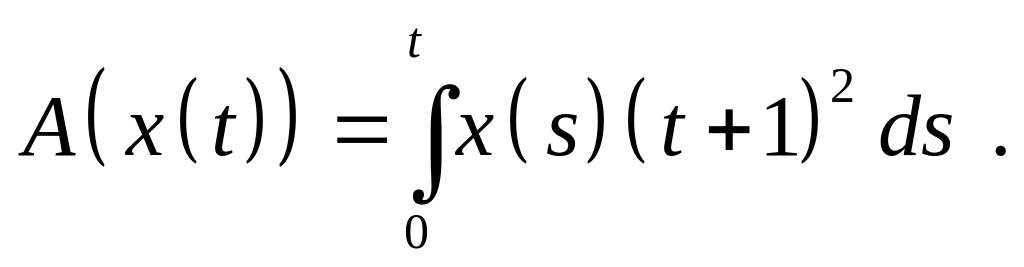
,
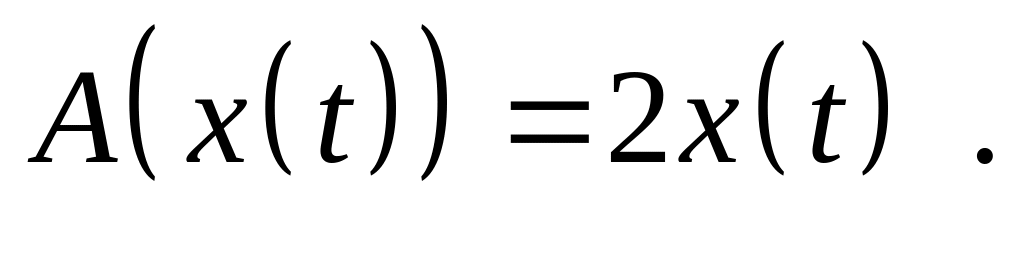
,
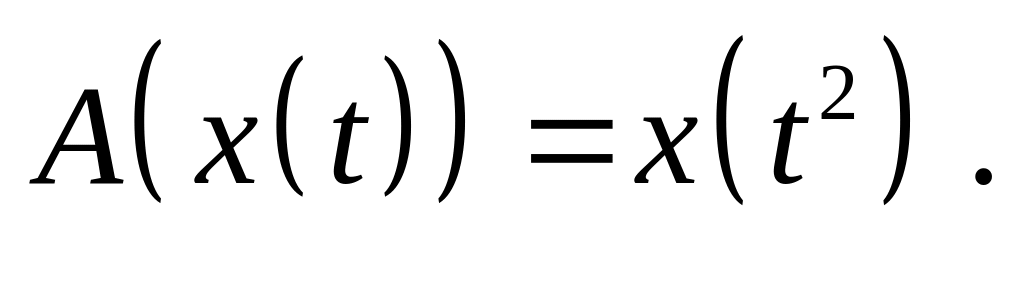
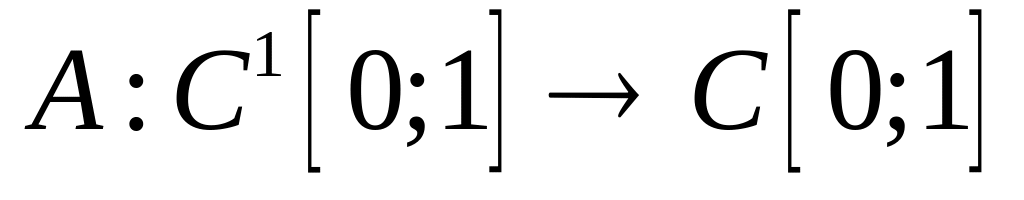 ,
,
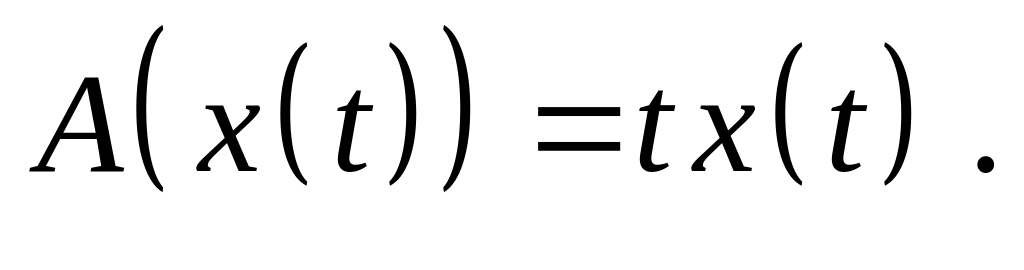
,
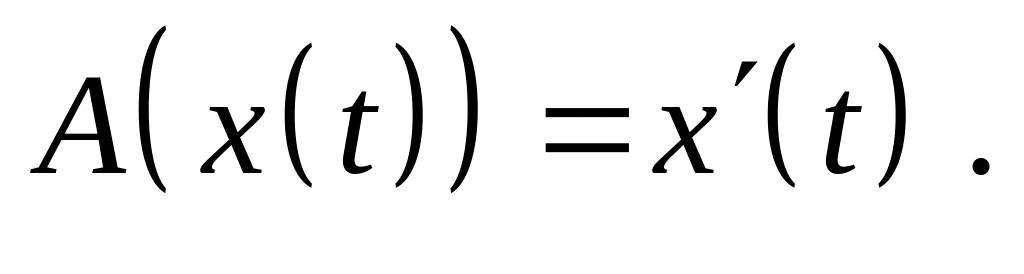
,
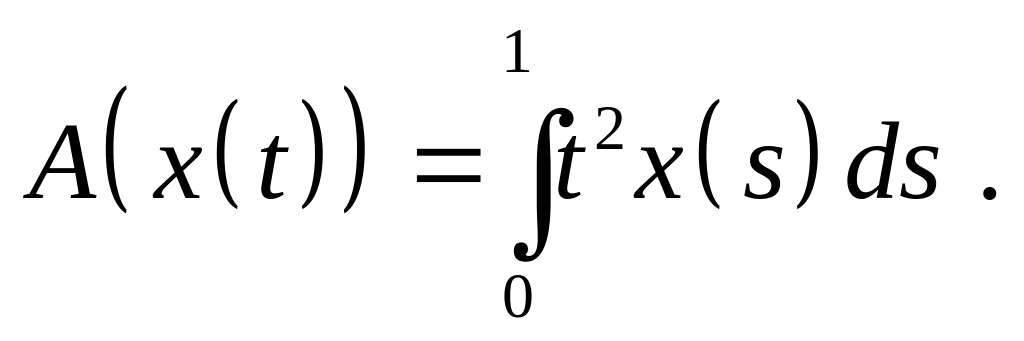
,
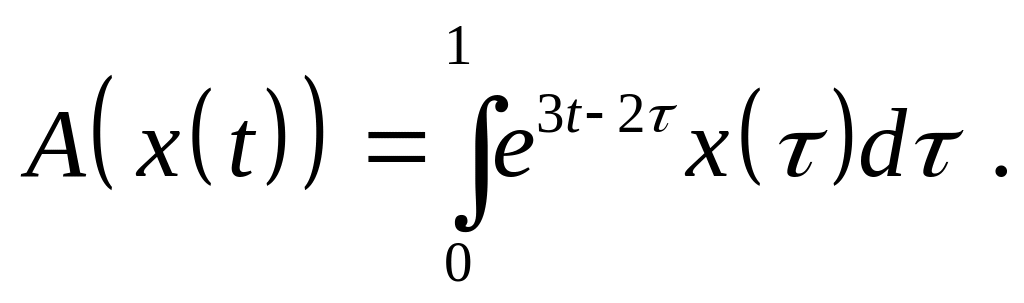
,
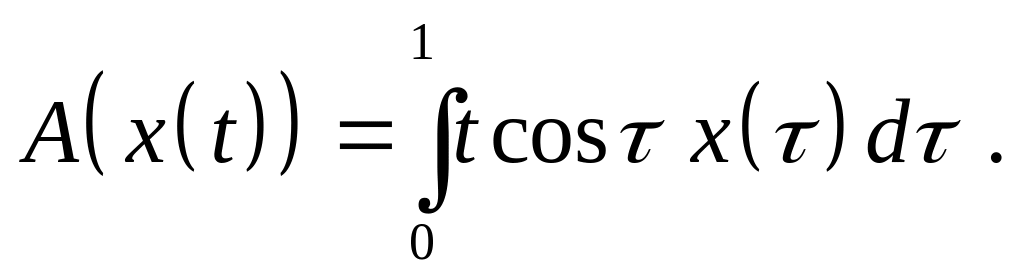
,
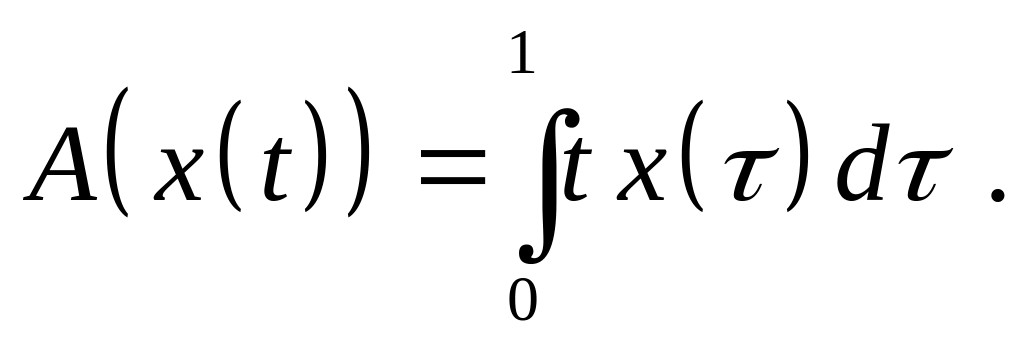
,
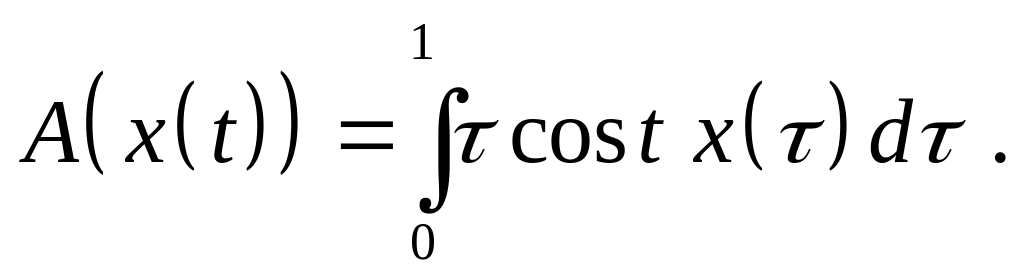
,
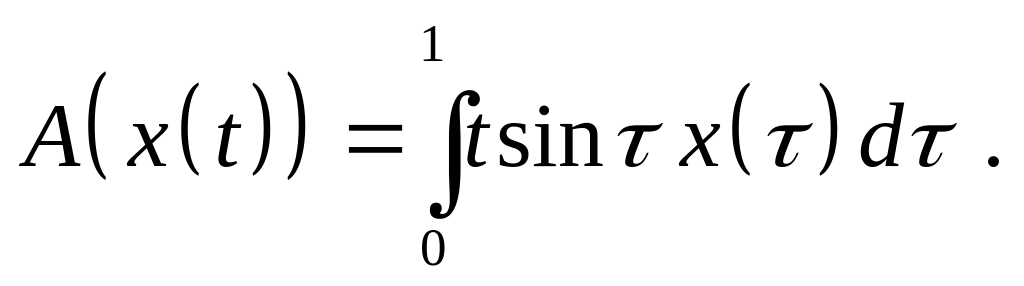
,
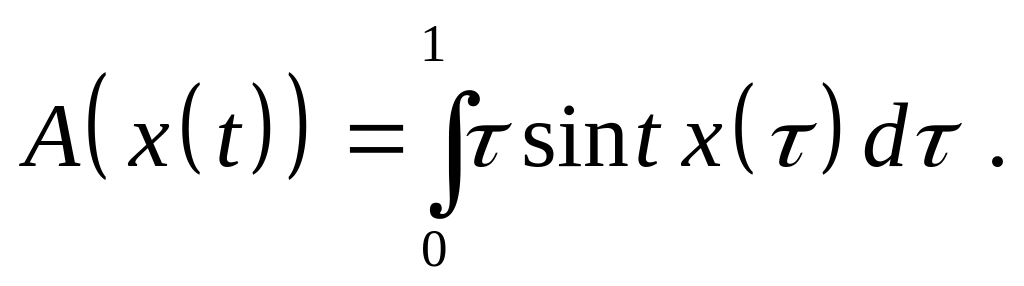
,
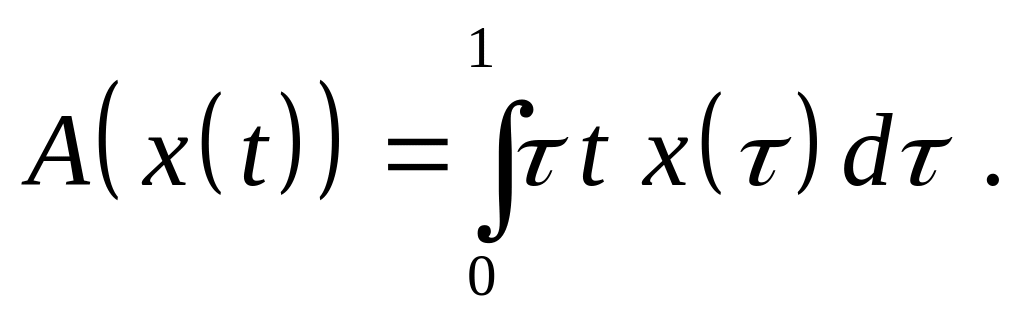
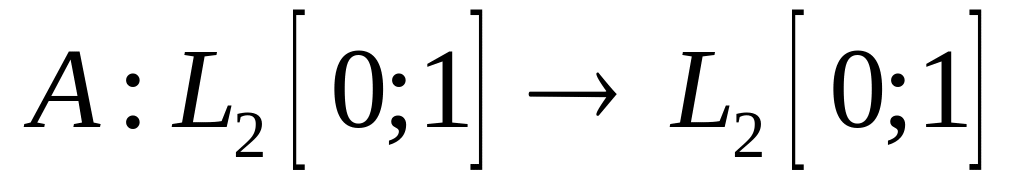 ,
,
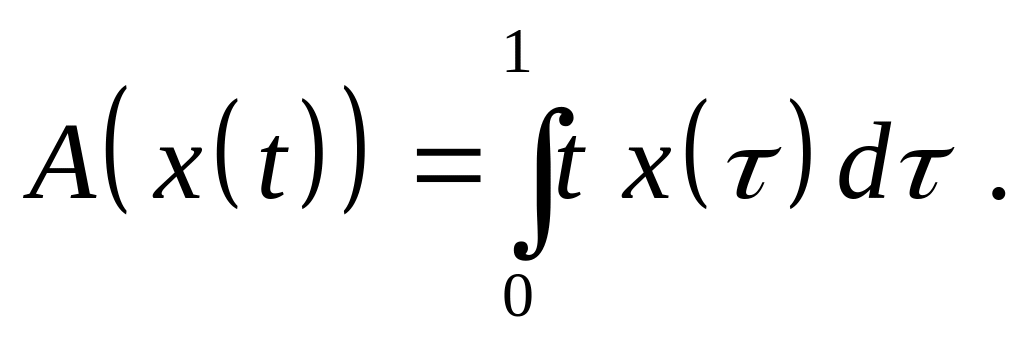
,
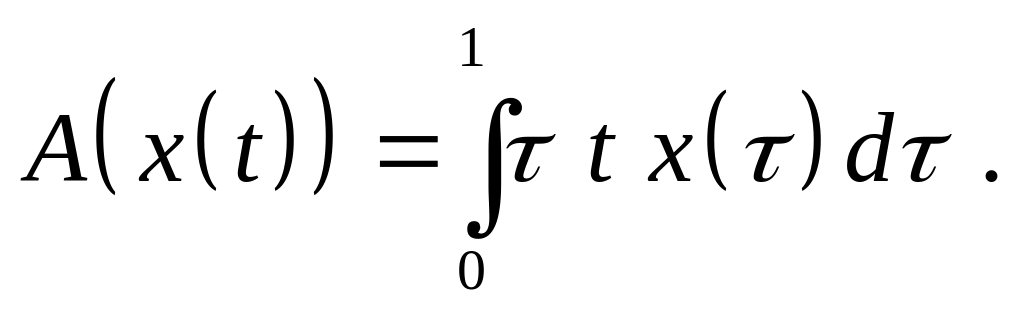
,
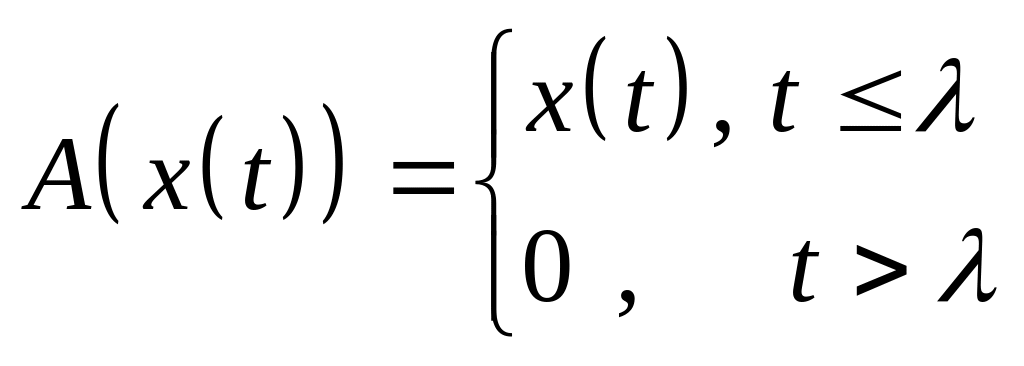 ,
где
,
где
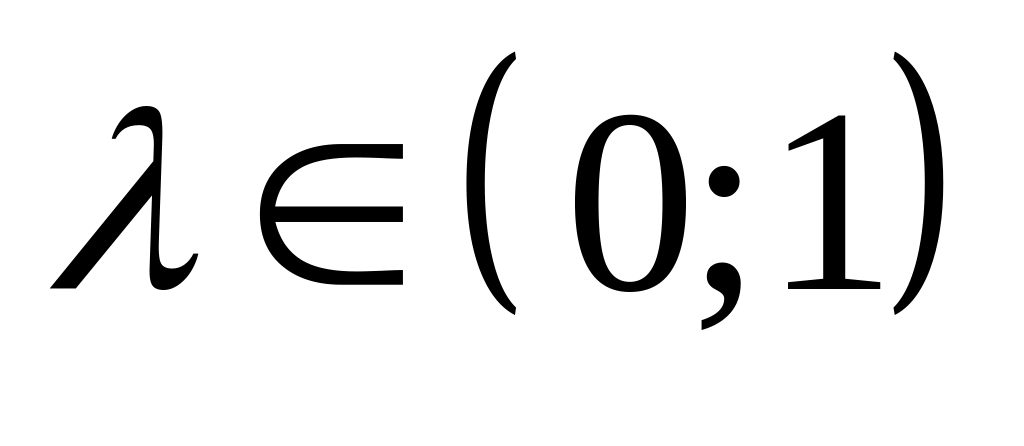 .
.,
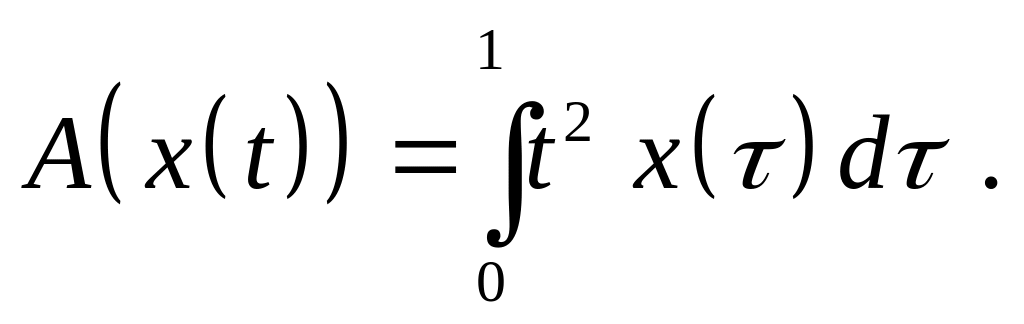
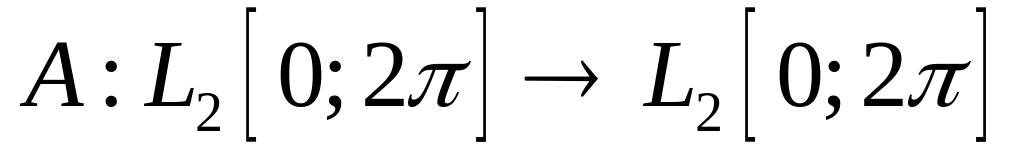 ,
,
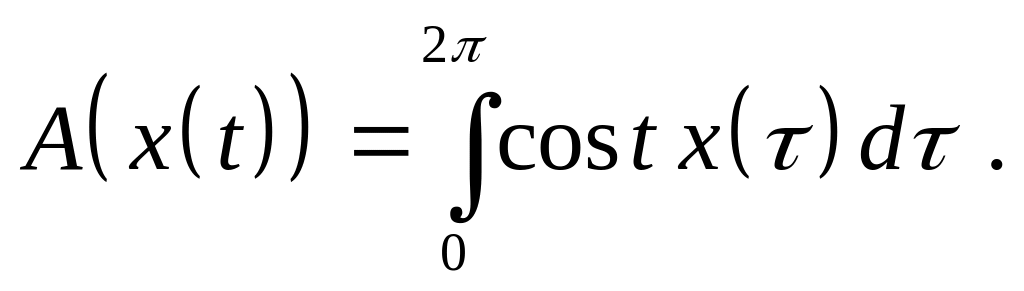
,
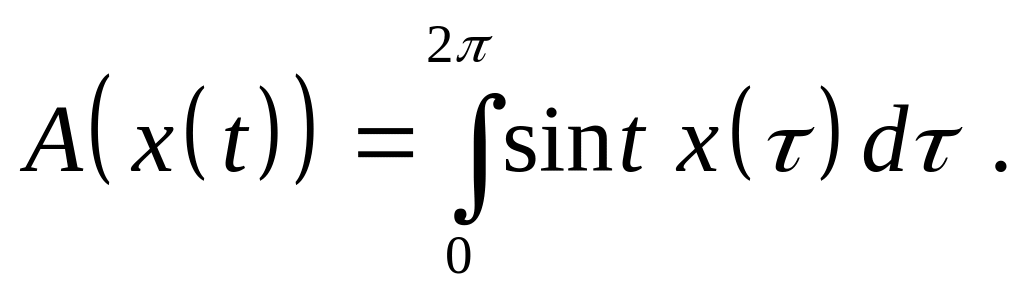
,
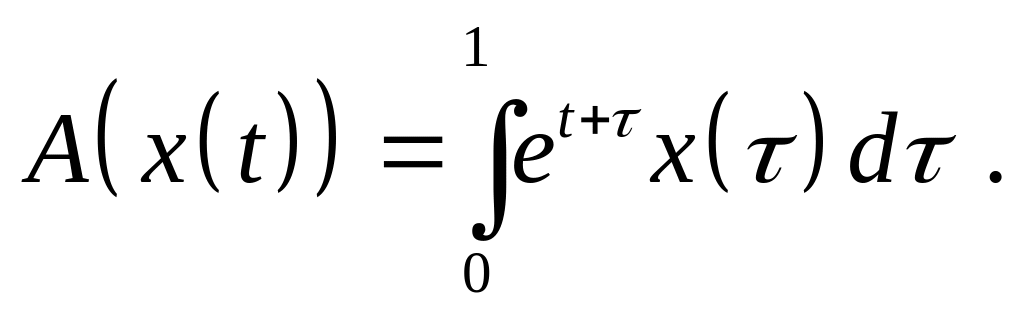
ЗАДАНИЕ 8
Определить общий вид решения интегрального уравнения и методом неопределенных коэффициентов найти его:
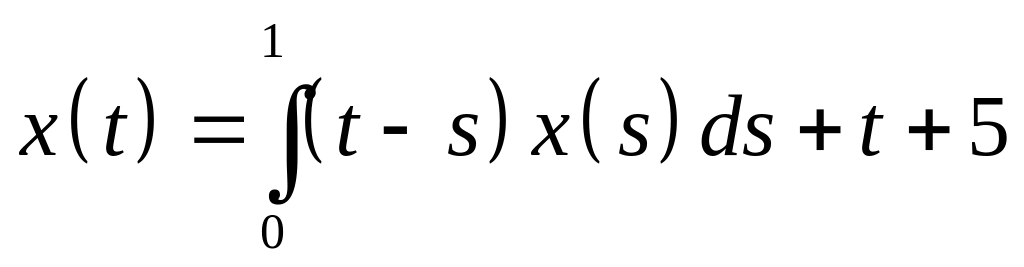 .
.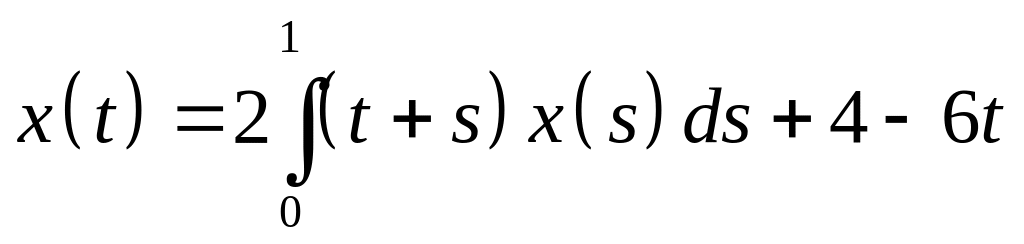 .
.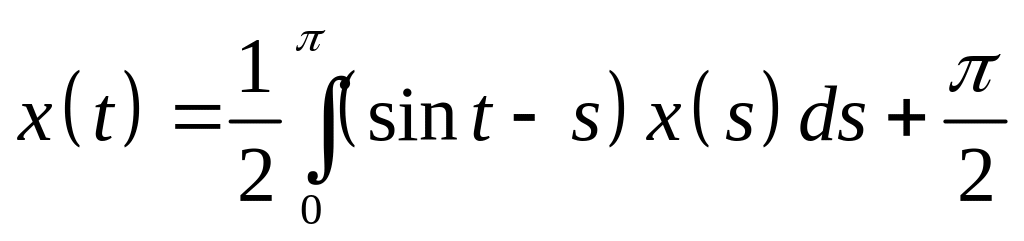 .
.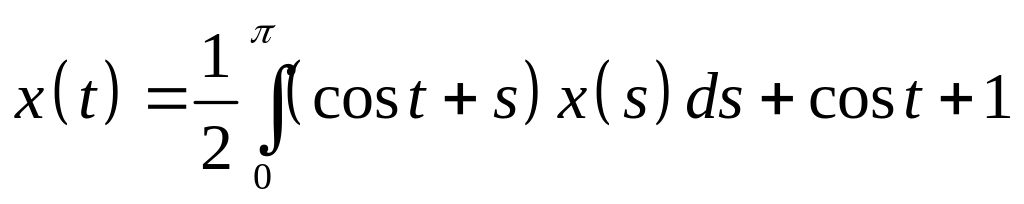 .
.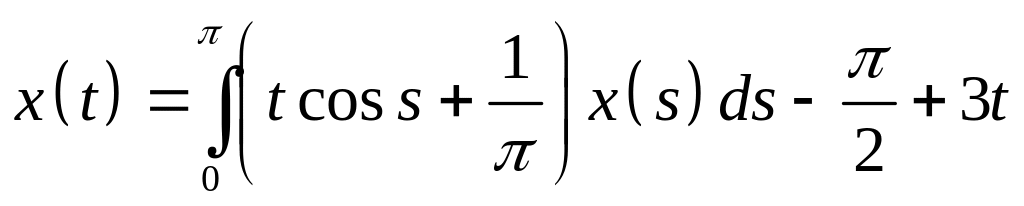 .
.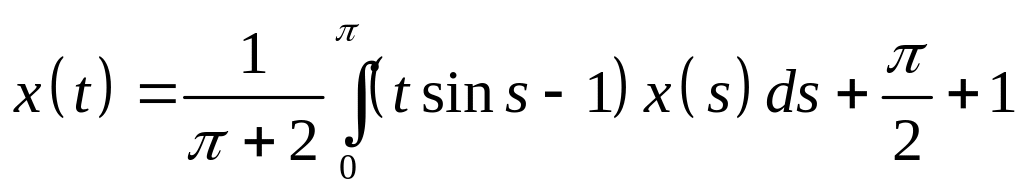 .
.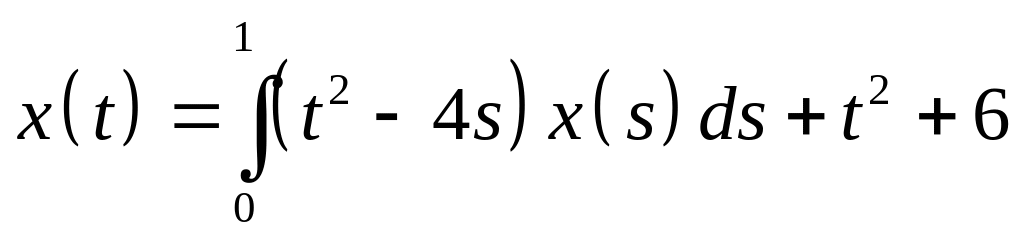 .
.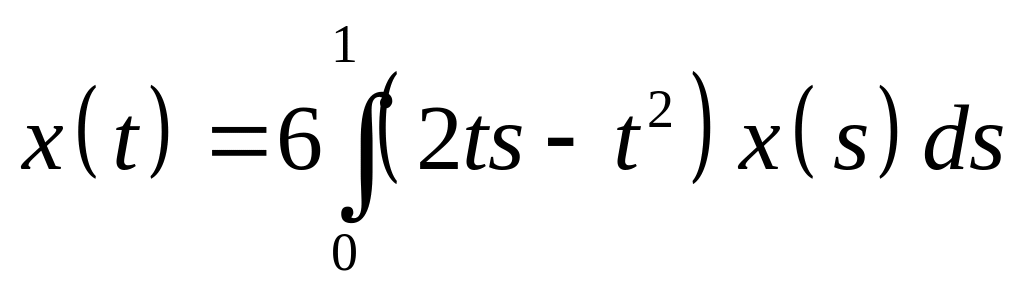 .
.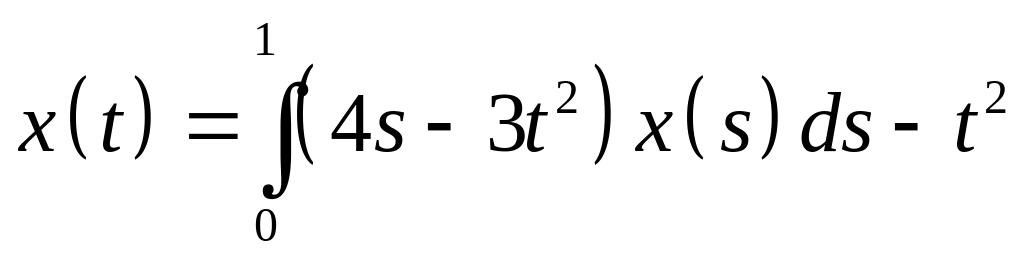 .
.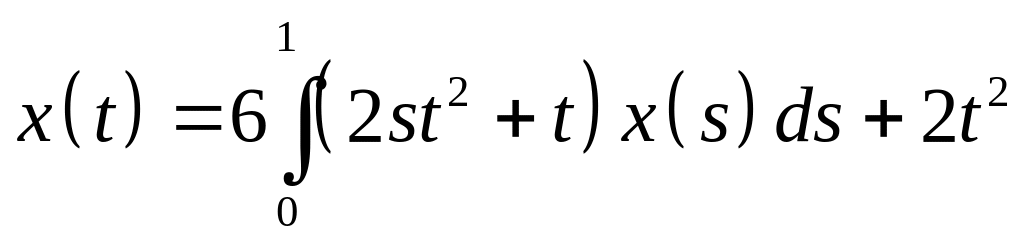 .
.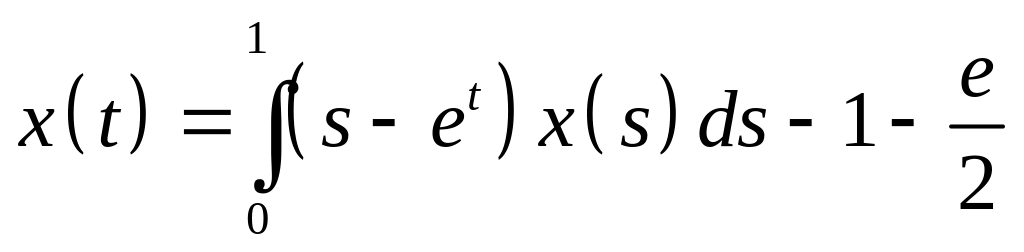 .
.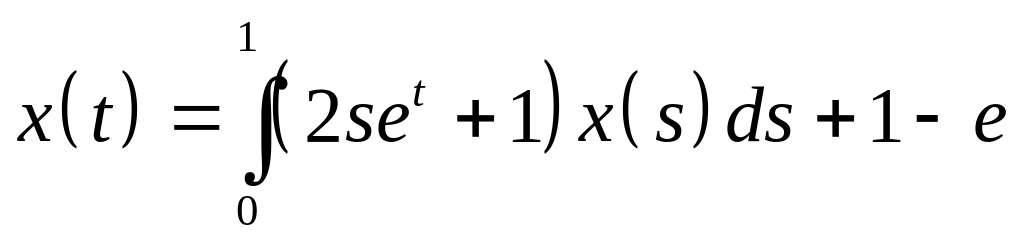 .
.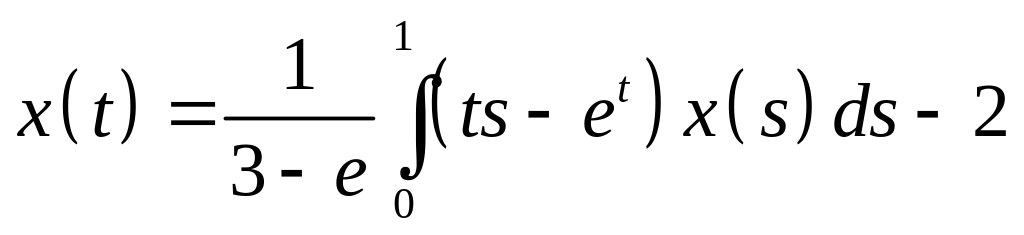 .
.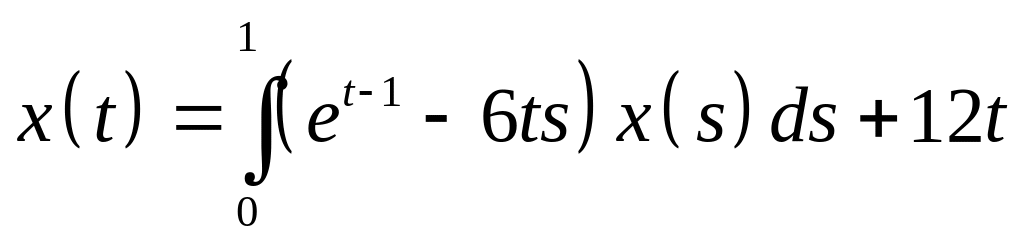 .
.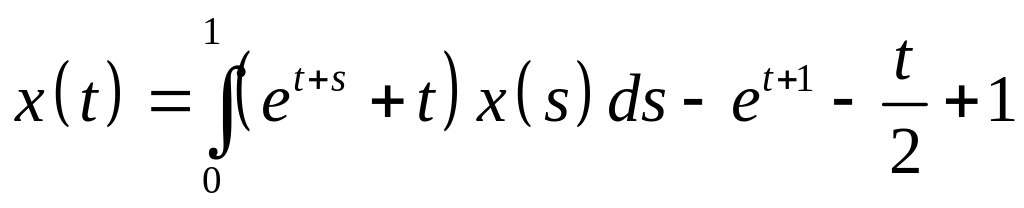 .
.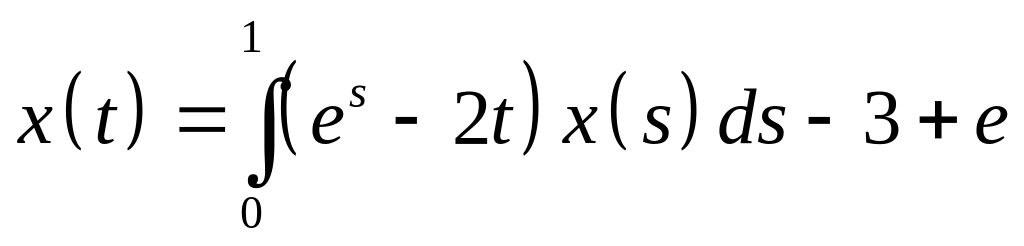 .
.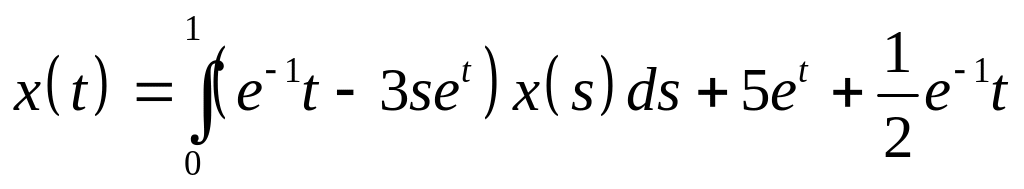 .
.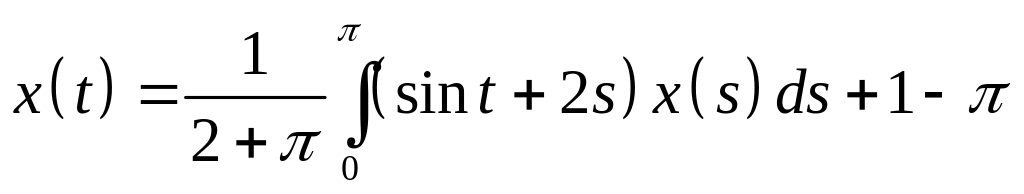 .
.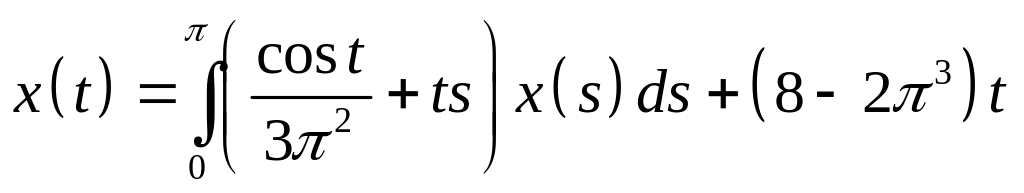 .
.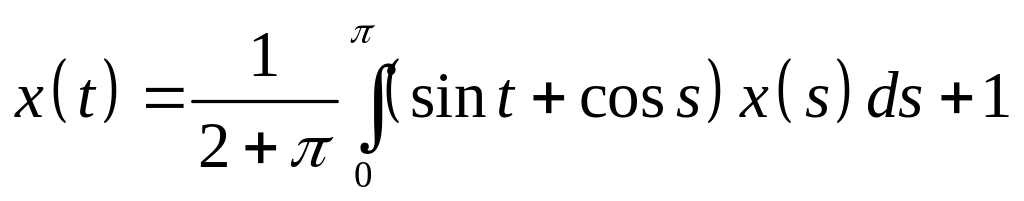 .
.
ЗАДАНИЕ 9
Решить интегральное уравнение с вырожденным ядром:
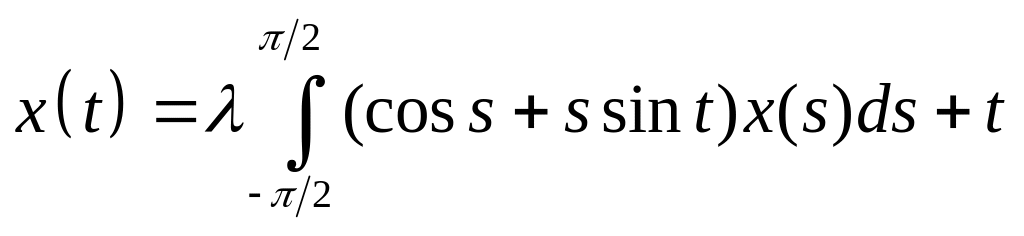 .
.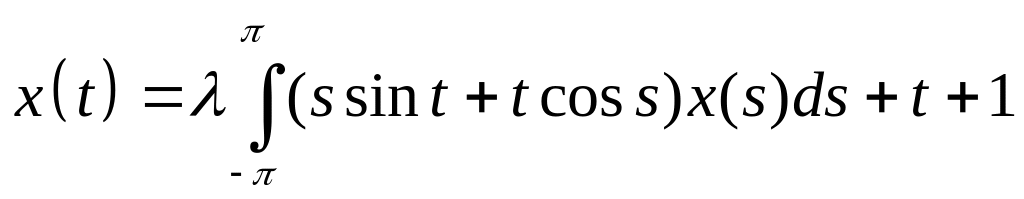 .
.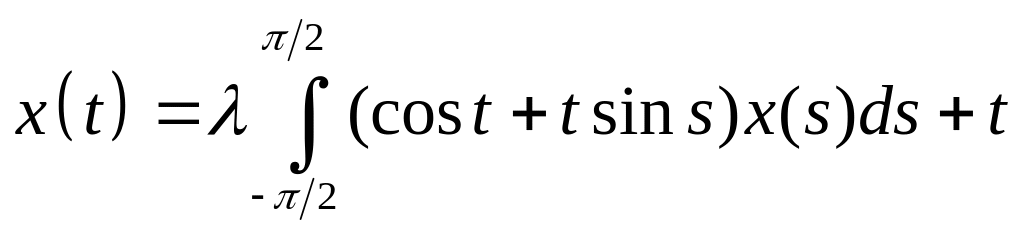 .
.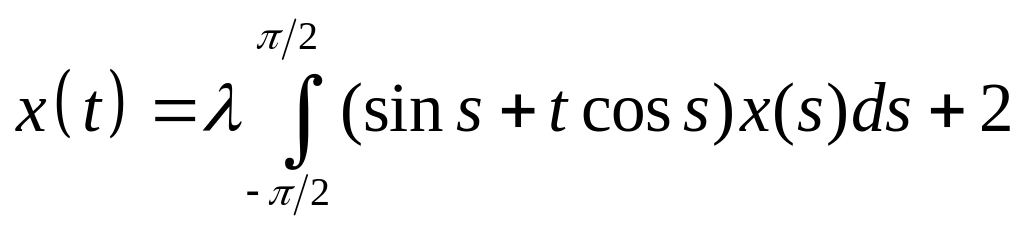 .
.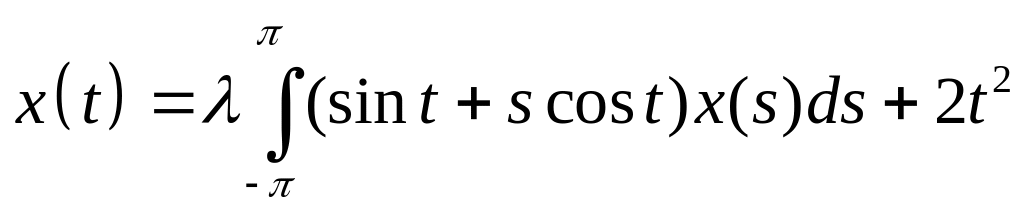 .
.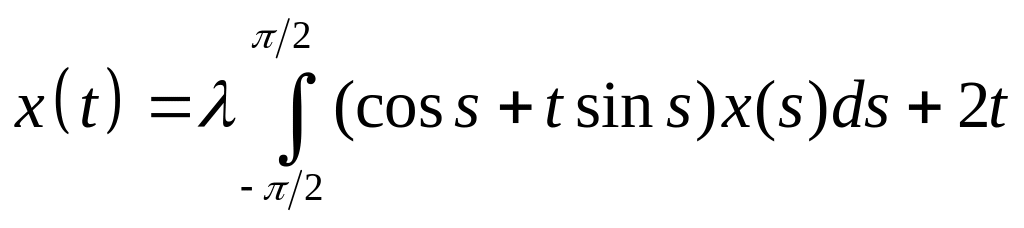 .
.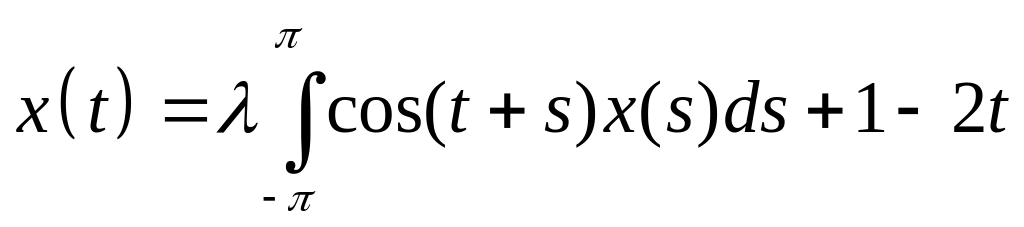 .
.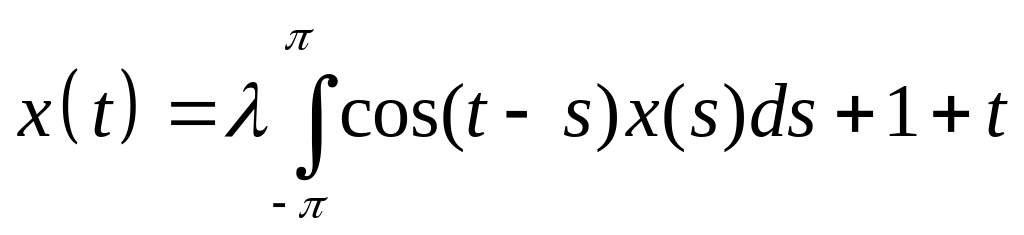 .
.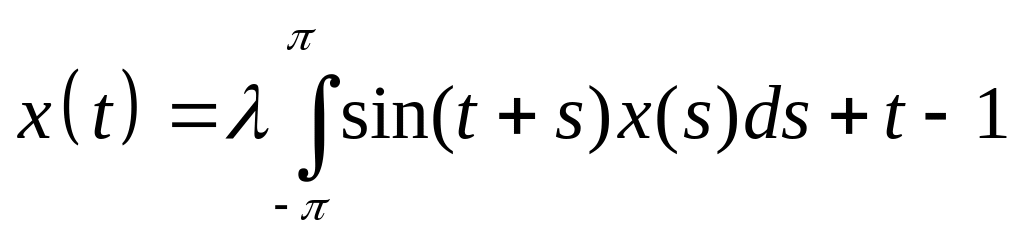 .
.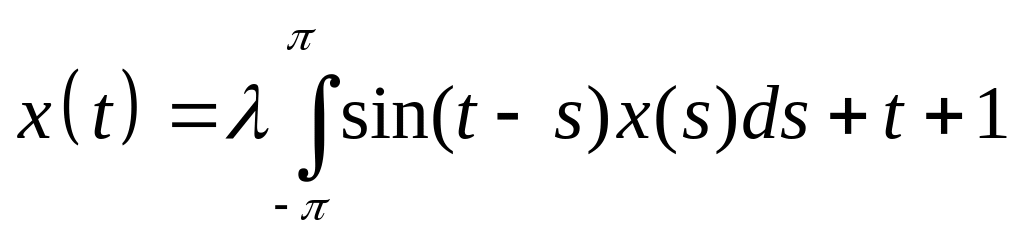 .
.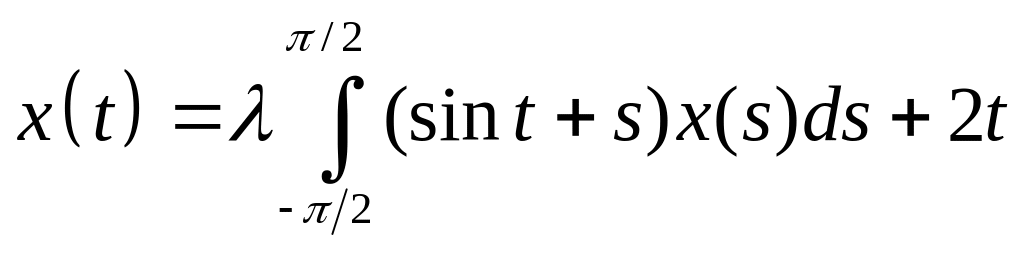 .
.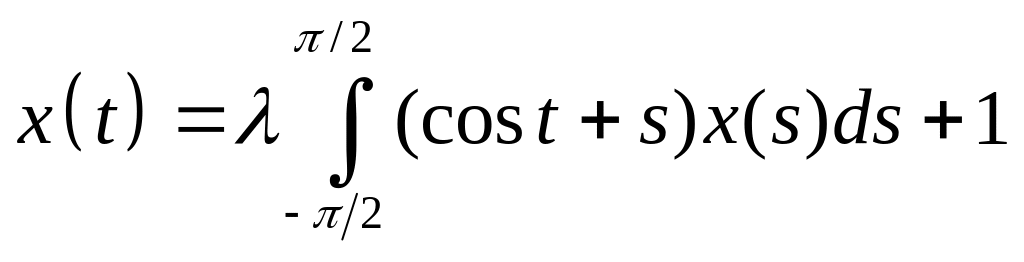 .
.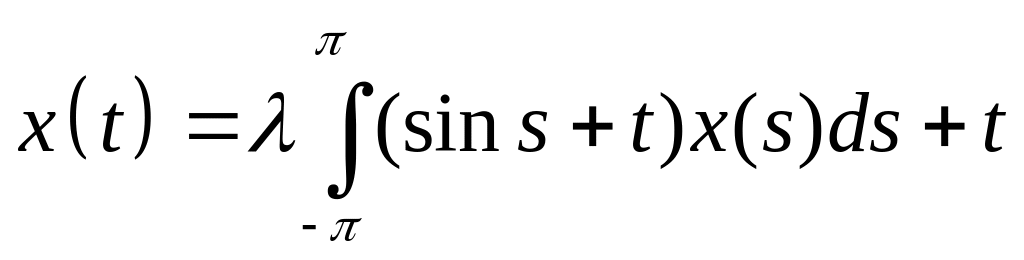 .
.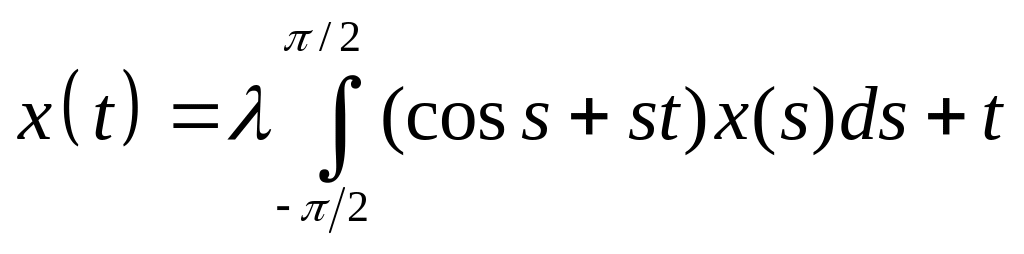 .
.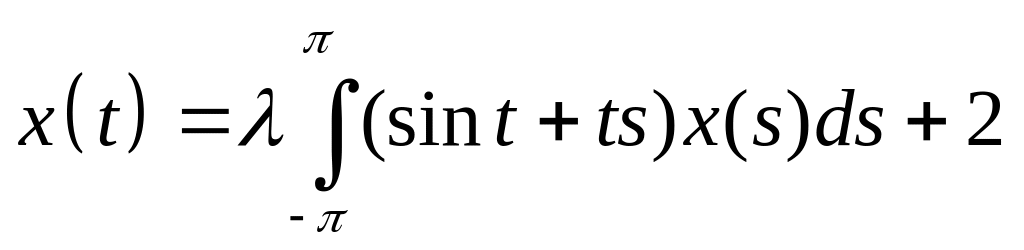 .
.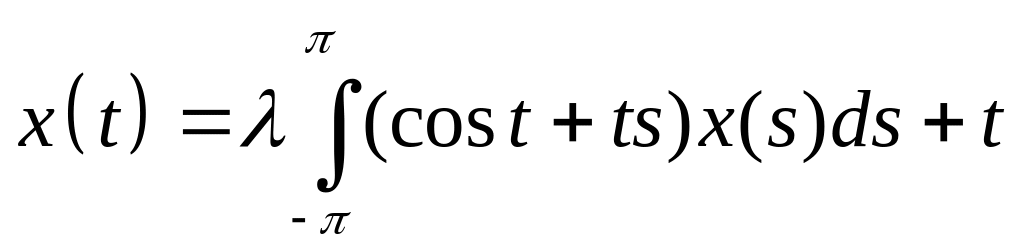 .
.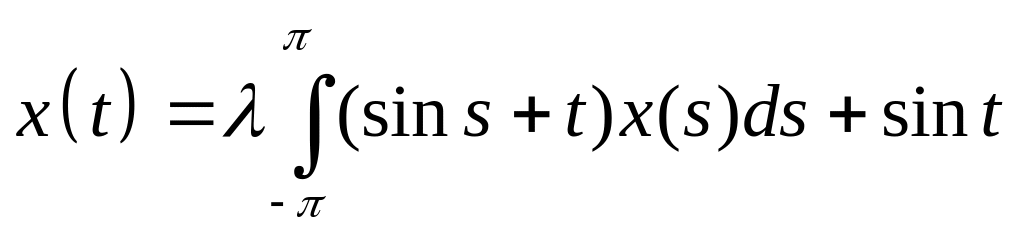 .
.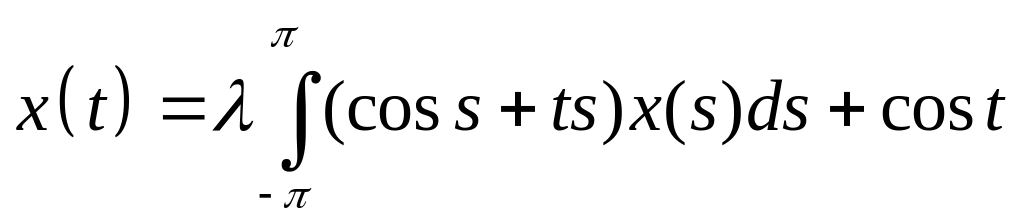 .
.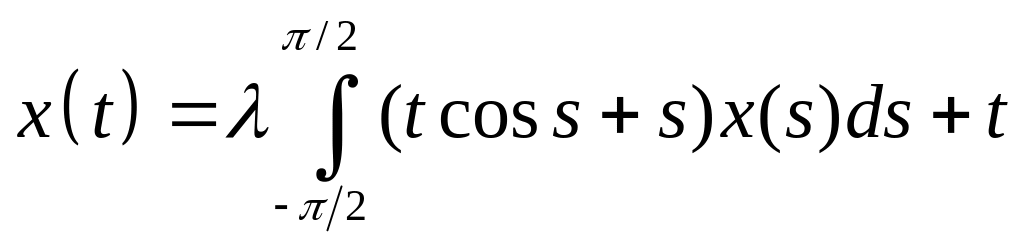 .
.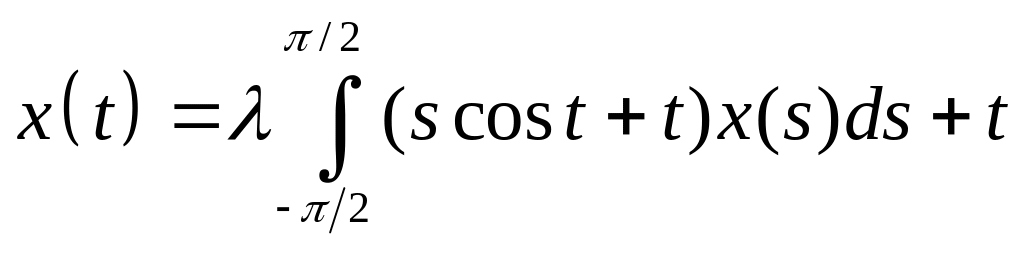 .
.
ЗАДАНИЕ 10
Найти резольвенту интегрального уравнения и с ее помощью решить его:
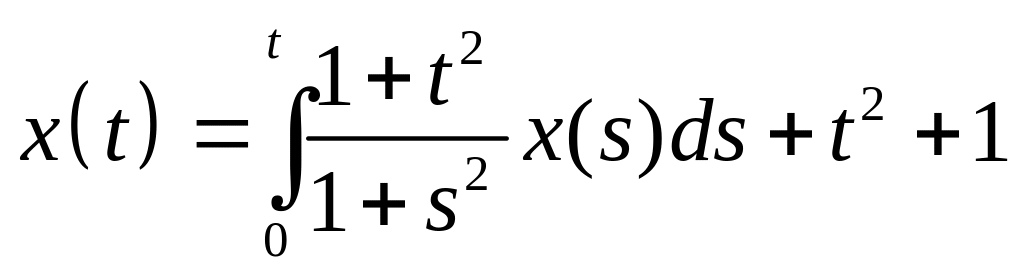 .
.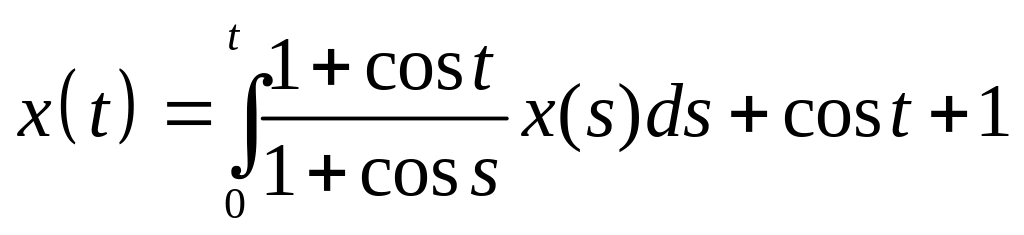 .
.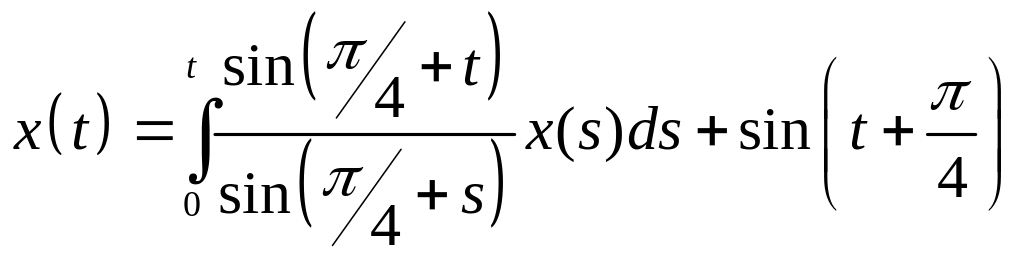 .
.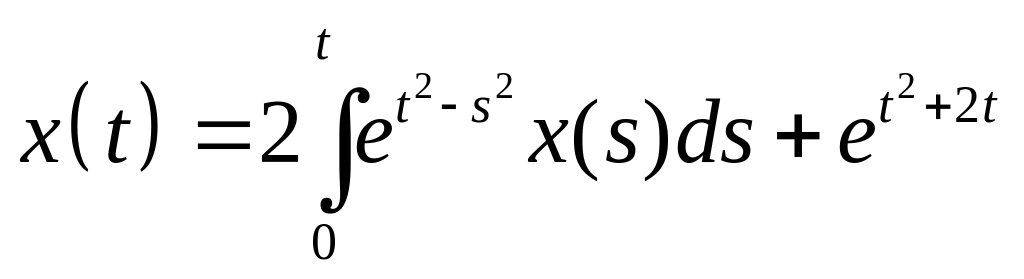 .
.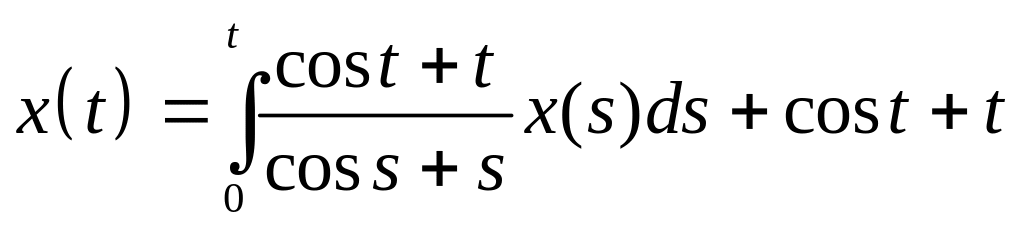 .
.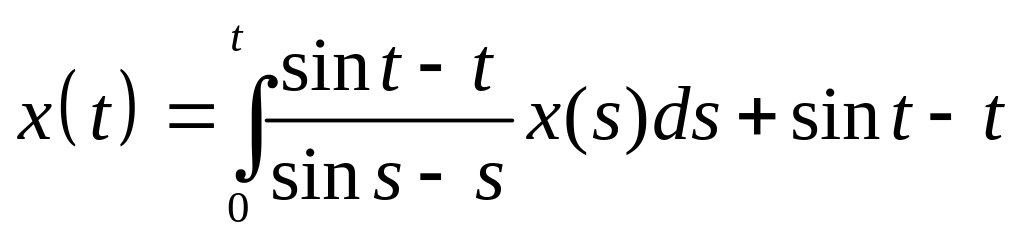 .
.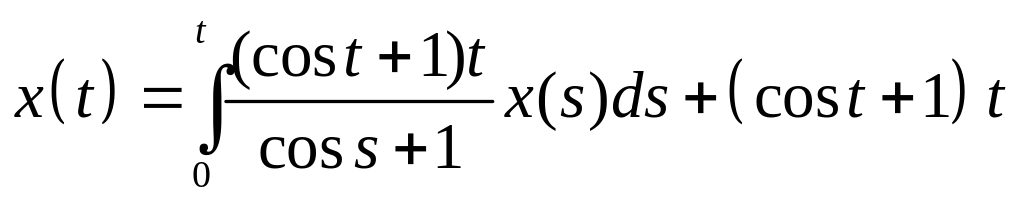 .
.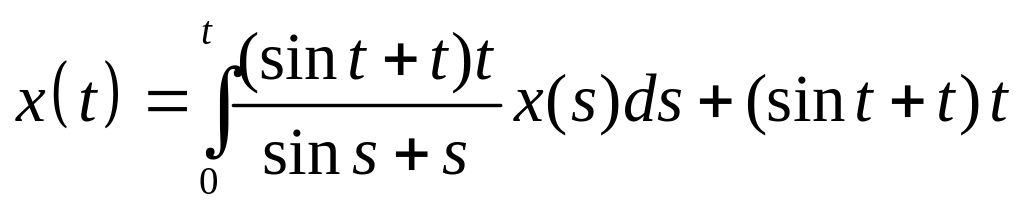 .
.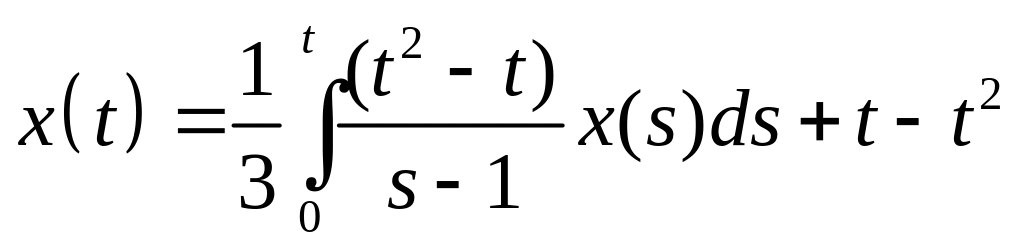 .
.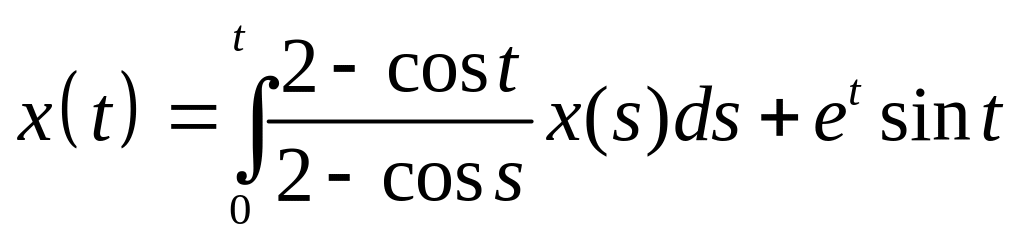 .
.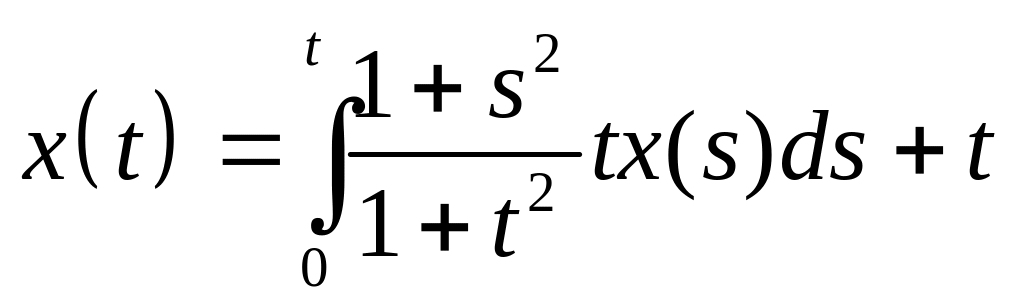 .
.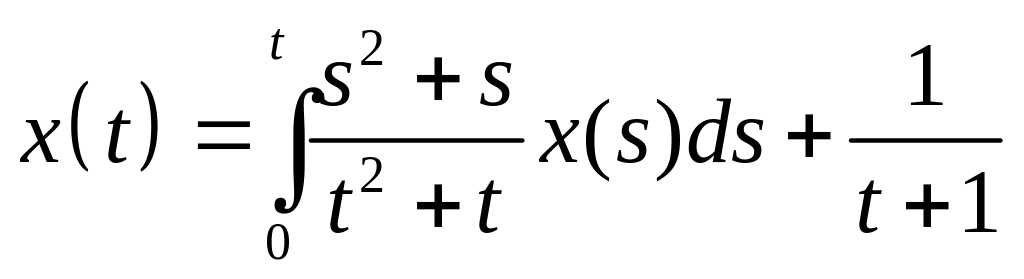 .
.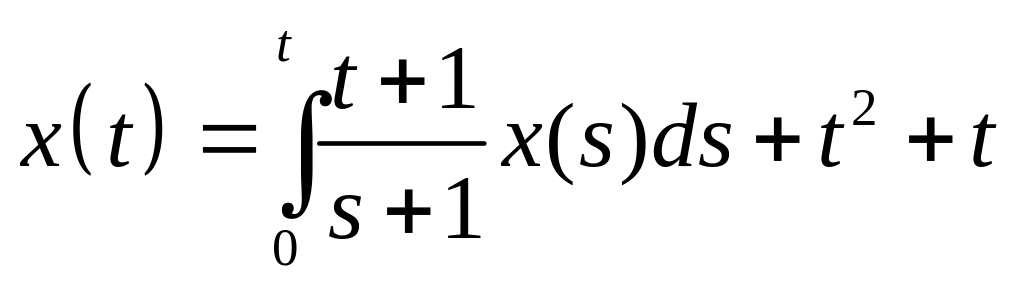 .
.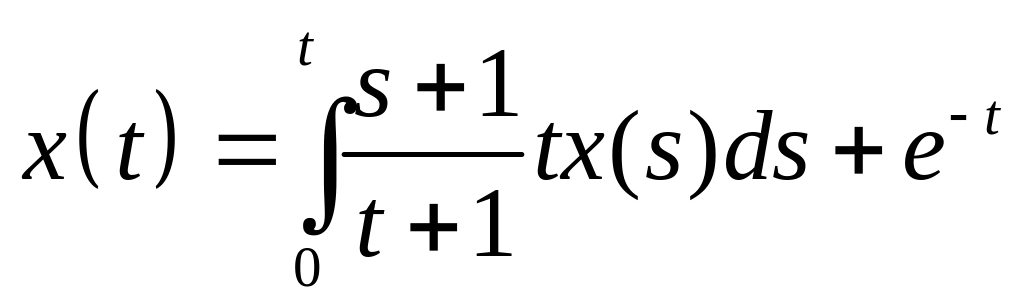 .
.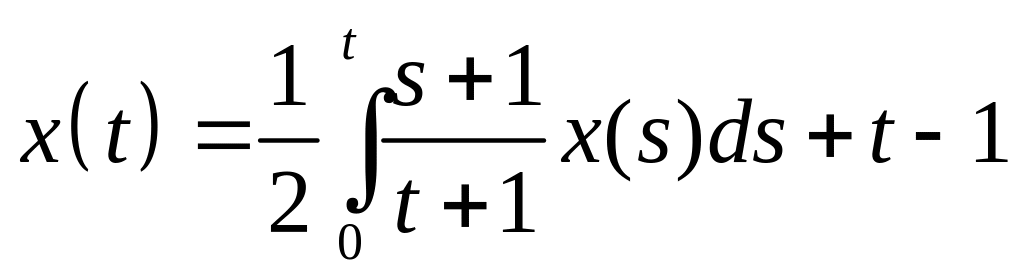 .
.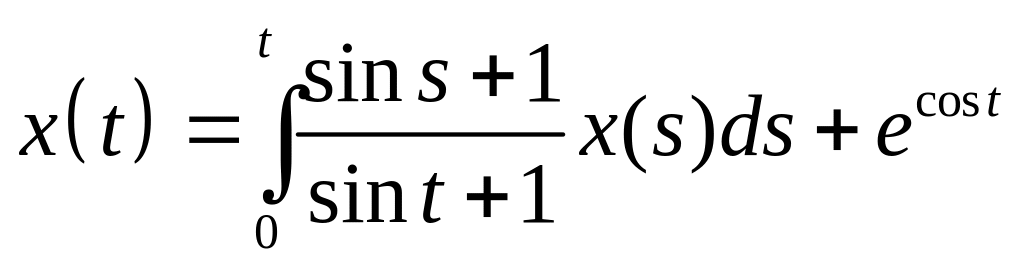 .
.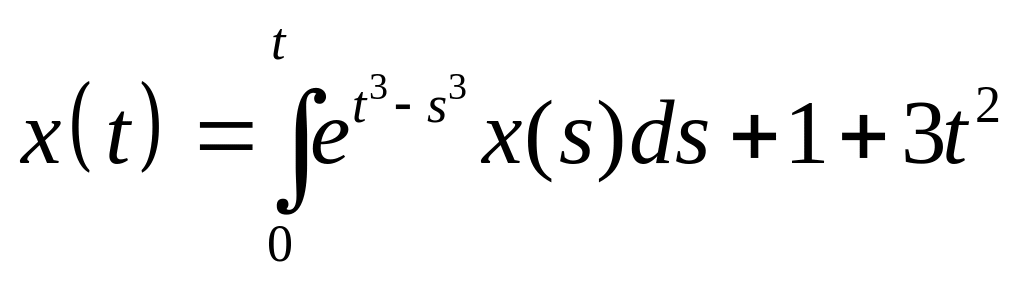 .
.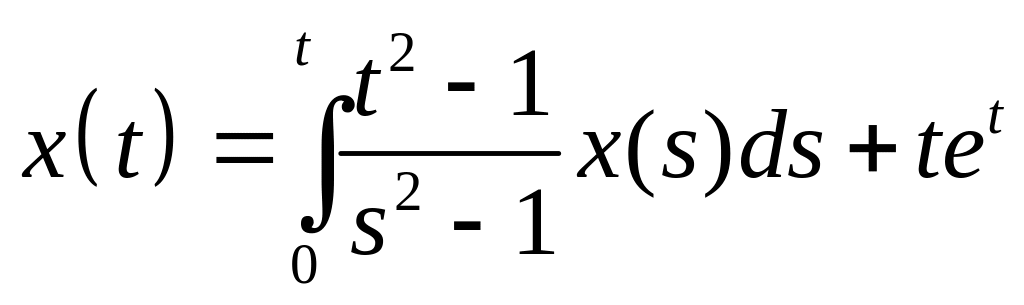 .
.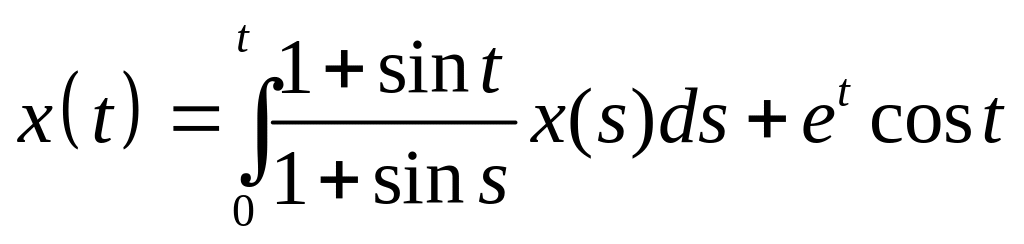 .
.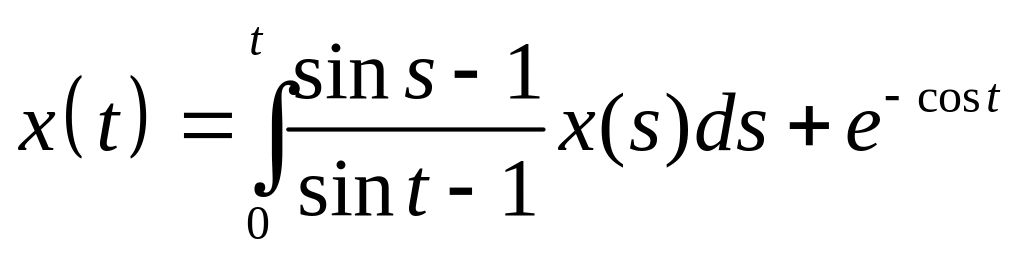
ЗАДАНИЕ 11
Исследовать на экстремум функционал:
ЗАДАНИЕ 12
Интегрируема
ли по Риману функция
![]() на отрезке
на отрезке
![]() ?
Интегрируема ли она по Лебегу относительно
меры Лебега
?
Интегрируема ли она по Лебегу относительно
меры Лебега
![]() на
?
Если функция интегрируема по Лебегу,
то найти
на
?
Если функция интегрируема по Лебегу,
то найти
![]() .
.
Примеры решения задач
ЗАДАЧА 1
Доказать,
что пространство
![]() непрерывных на
непрерывных на
![]() функций с расстоянием
функций с расстоянием
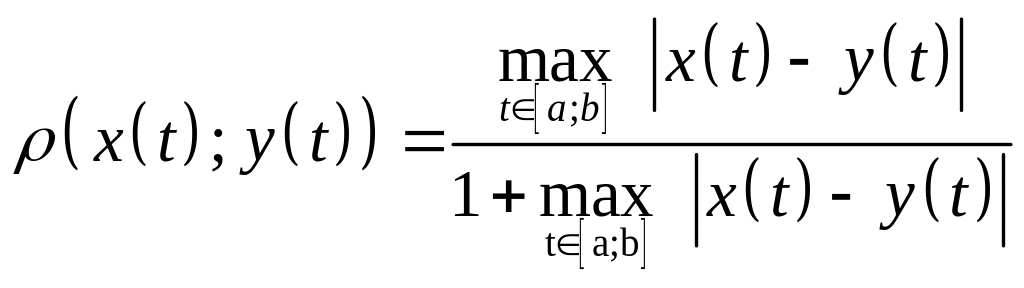 является метрическим.
является метрическим.
РЕШЕНИЕ
Для того чтобы доказать, что пространство является метрическим, покажем, что выполняются все аксиомы метрики:
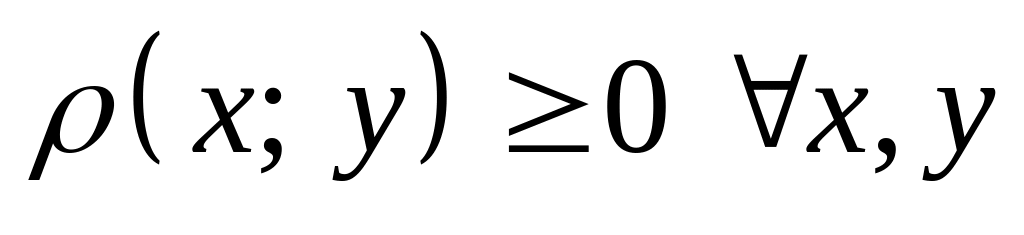 ,
причем
,
причем
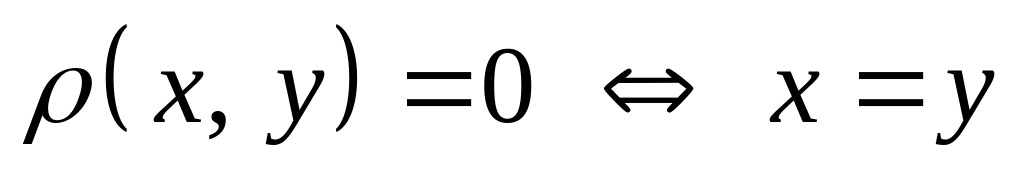 ;
;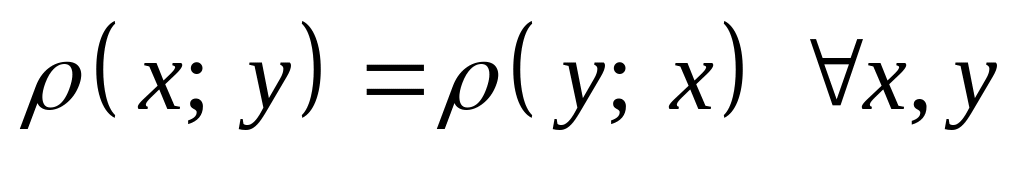 ;
;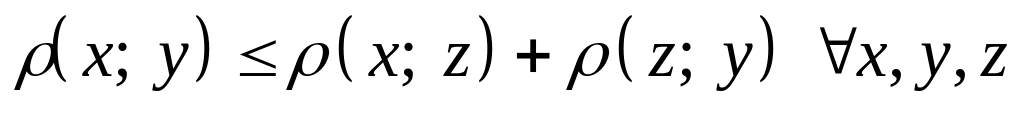 ;
;
Итак,
так как
![]() ,
то
,
то
![]() .
Следовательно,
.
Следовательно,
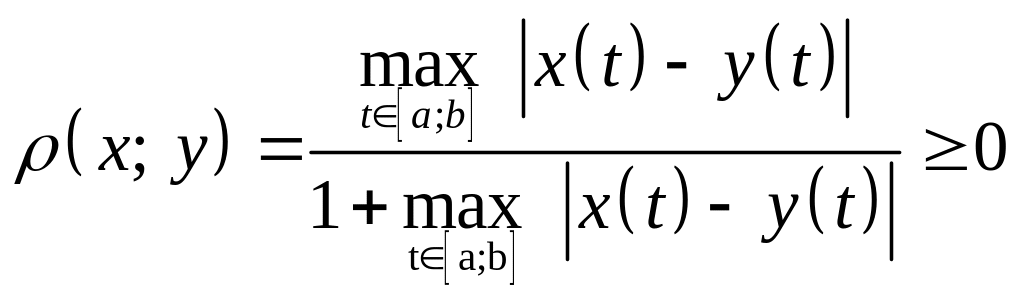 .
.
Причем,
если
![]() ,
то
,
то
![]() ,
и
,
и
![]() .
Обратно, если
,
то
.
Обратно, если
,
то
![]() .
Следовательно,
,
т.е.
.
.
Следовательно,
,
т.е.
.
Таким образом, 1-ая аксиома выполняется. Теперь вторая:
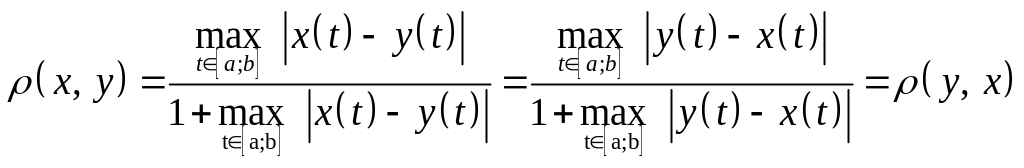 .
.
Для доказательства выполнимости третьей аксиомы, рассмотрим следующее неравенство:
![]() ;
следовательно,
;
следовательно,
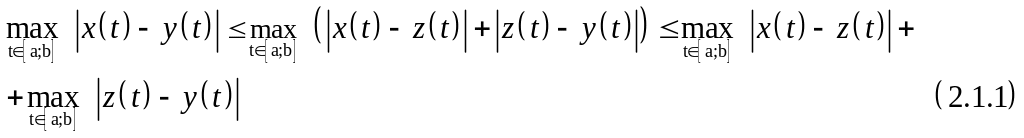
Так
как производная
![]() функции
функции
![]() положительна
положительна
![]() ,
следовательно сама
,
следовательно сама
![]() монотонно возрастает. Поэтому, в силу
неравенства (2.1.1):
монотонно возрастает. Поэтому, в силу
неравенства (2.1.1):
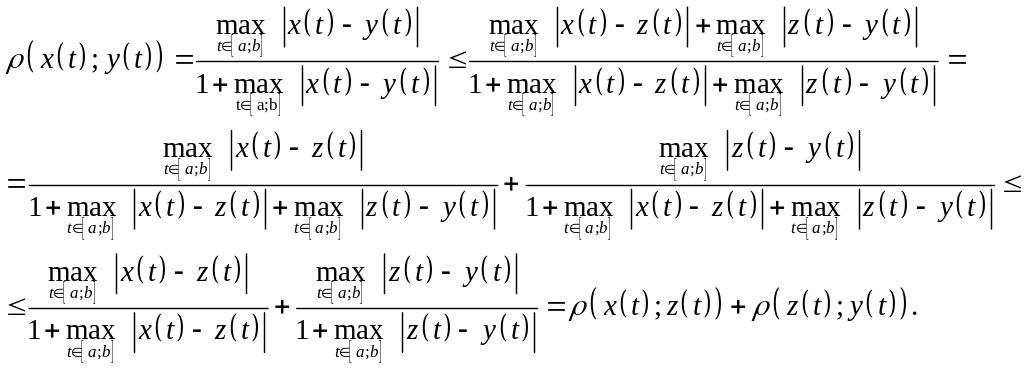
Таким образом, и третья аксиома выполняется, следовательно данное пространство является метрическим.