
- •Задание 1
- •Доказать, что формулой определяется метрика в .
- •Доказать, что формулой определяется метрика в .
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Задача 8
- •Задача 9
- •Задача 10
- •Задача 11
- •Задача 12
- •Библиографический список
- •Сборник индивидуальных заданий по функциональному анализу
- •426069, Г. Ижевск, ул. Студенческая, 7
Задание 4
Пусть
 и
и
 – некоторые подмножества топологического
пространства
,
причем замыкание множества
содержится в замыкании множества
– некоторые подмножества топологического
пространства
,
причем замыкание множества
содержится в замыкании множества
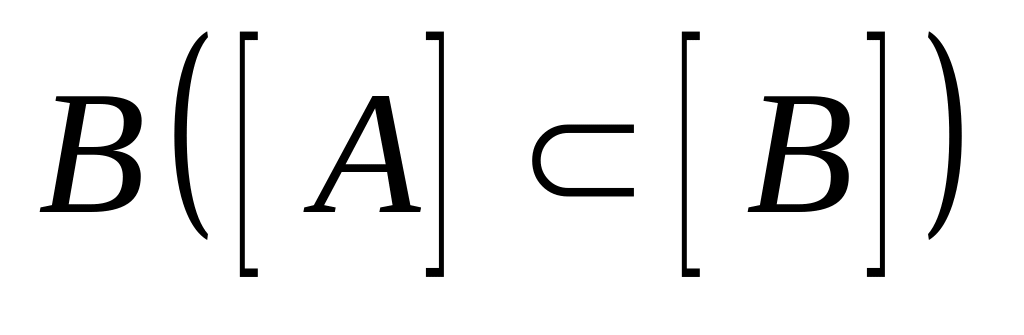 .
Можно ли утверждать, что всегда
является подмножеством
.
Можно ли утверждать, что всегда
является подмножеством
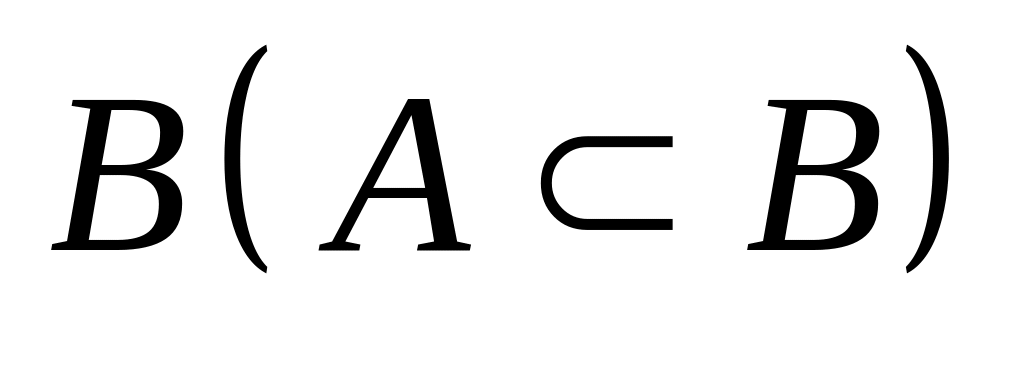 ?
?Пусть
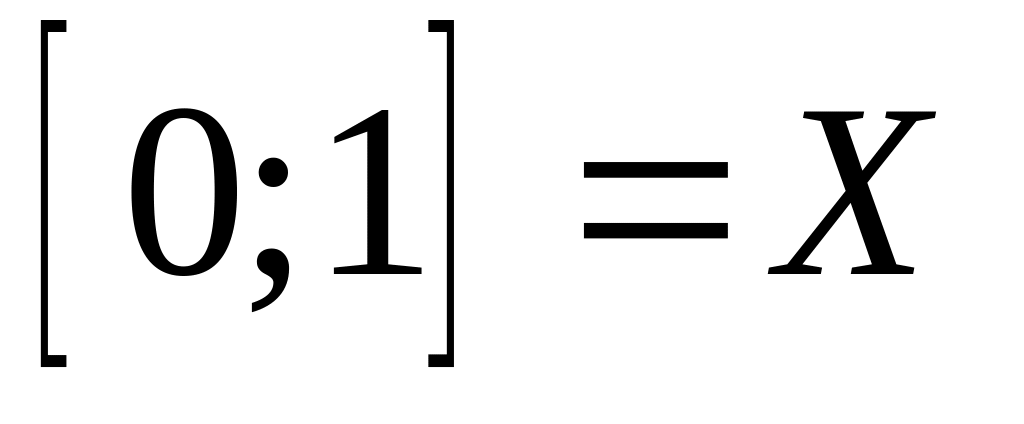 ,
а открытыми в нем являются те его
подмножества (наряду с
и
,
а открытыми в нем являются те его
подмножества (наряду с
и
 ),
которые получаются выбрасыванием из
него любого конечного или счетного
числа точек. Доказать, что:
),
которые получаются выбрасыванием из
него любого конечного или счетного
числа точек. Доказать, что:– топологическое пространство;
сходящимися в являются только те последовательности, элементы которых начиная с некоторого номера, совпадают.
Пусть , а открытыми в нем являются те его подмножества (наряду с и ), которые получаются выбрасыванием из него любого конечного или счетного числа точек. Доказать, что точка 0 является точкой прикосновения для множества
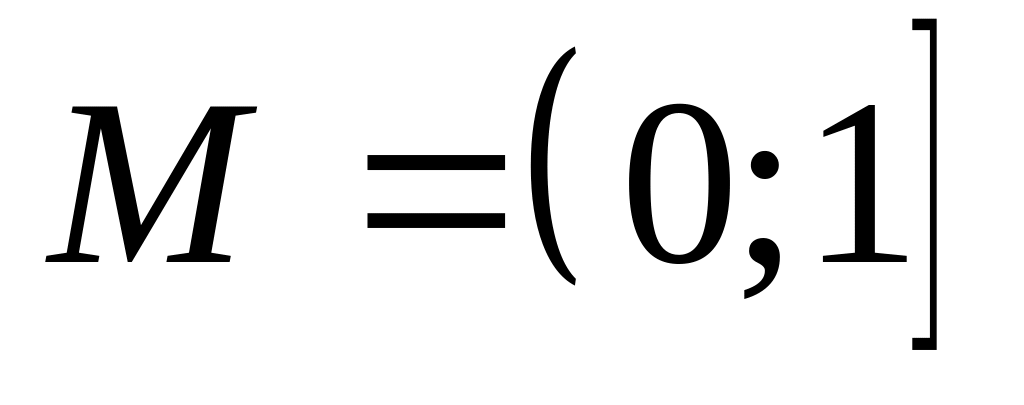 ,
но никакая последовательность из
,
но никакая последовательность из
 не сходится к 0 в
.
не сходится к 0 в
.Доказать, что в топологическом пространстве с тривиальной топологией каждая последовательность сходится к любой точке этого пространства.
Пусть
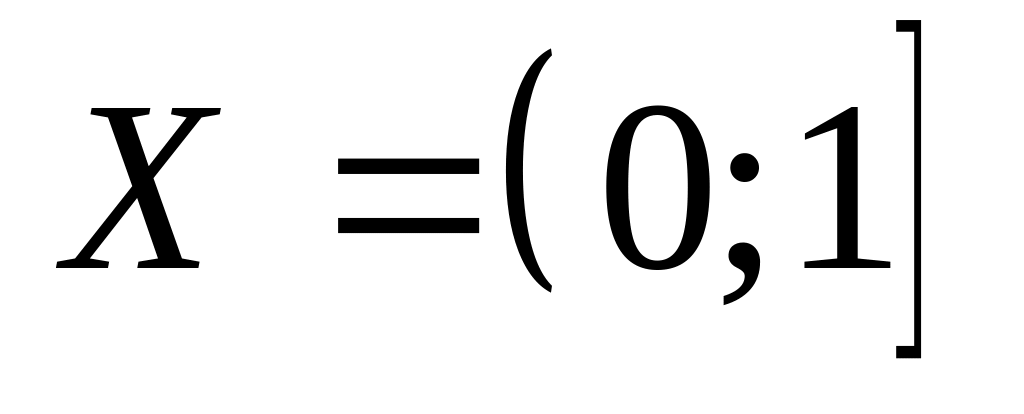 ,
а топология
,
а топология
 определяется множествами
,
,
интервалами
определяется множествами
,
,
интервалами
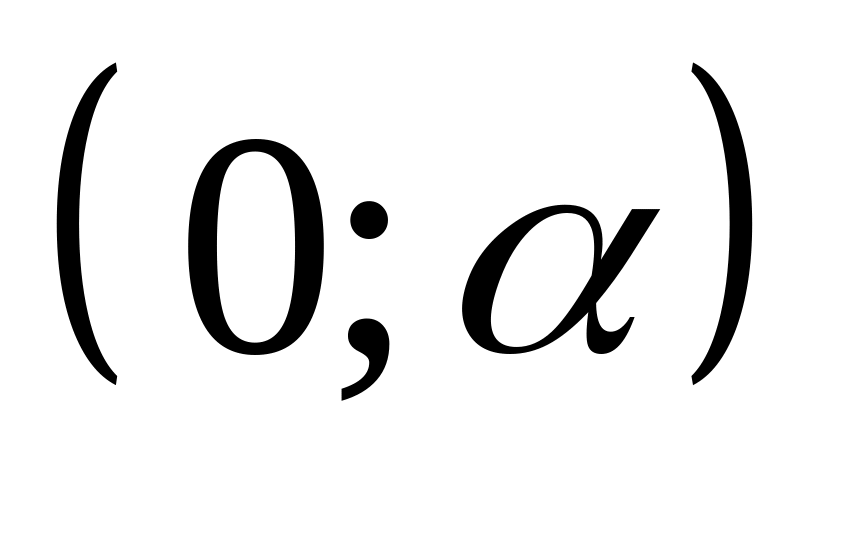 ,
где
,
где
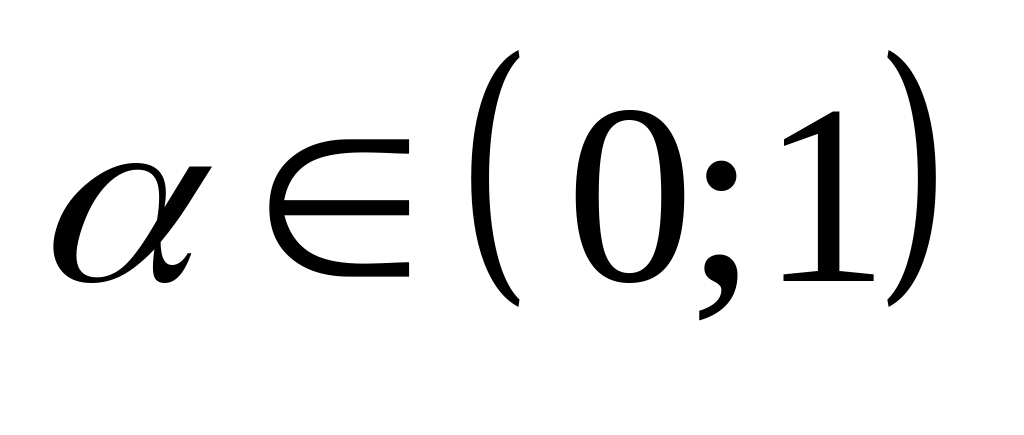 и множествами вида
и множествами вида
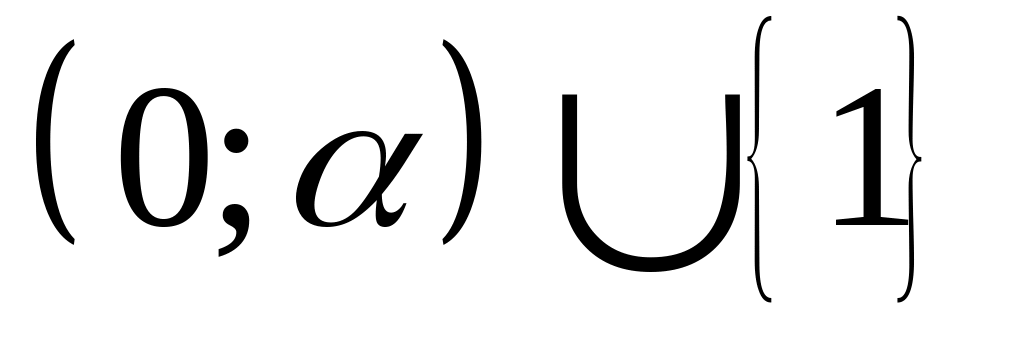 .
Доказать, что в пространстве
.
Доказать, что в пространстве
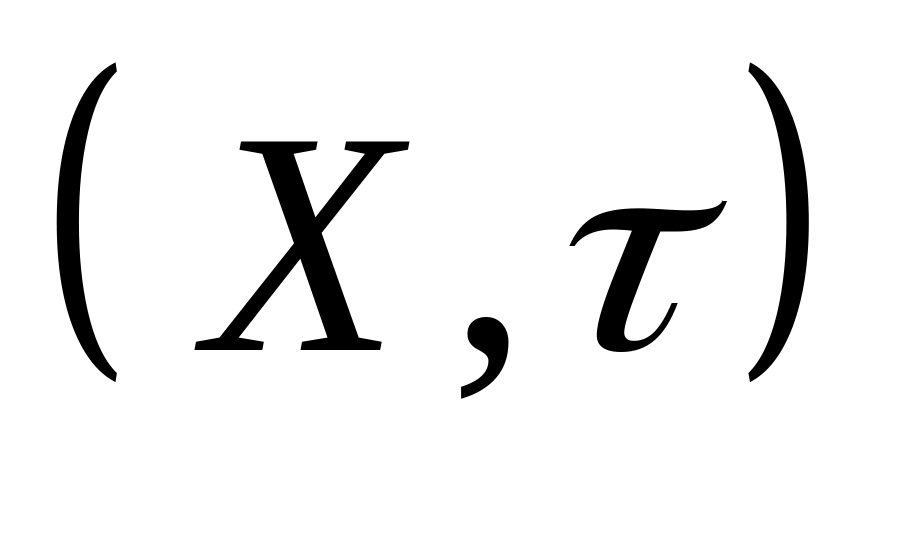 последовательность
последовательность
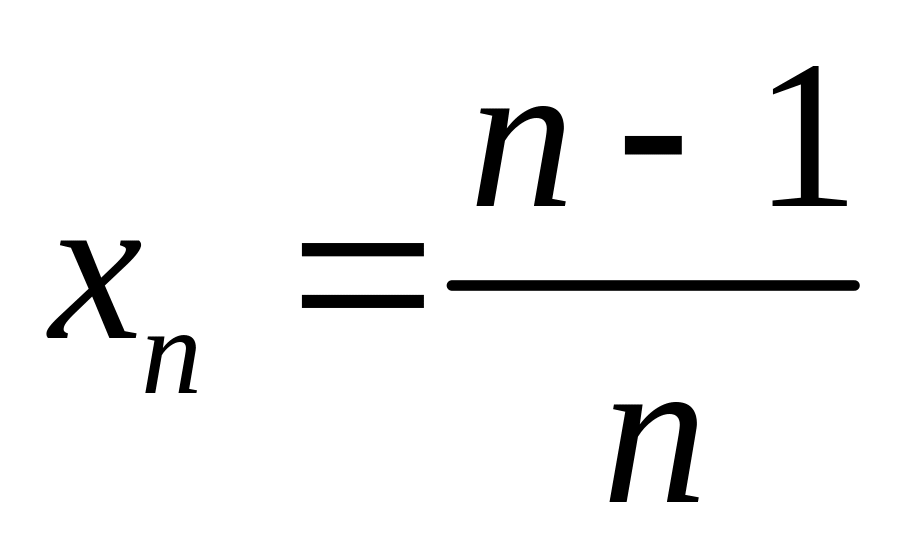 не имеет предела.
не имеет предела.Пусть
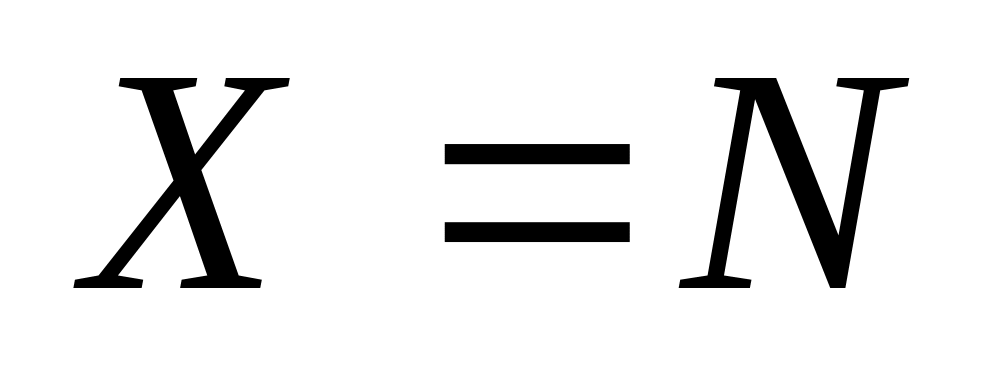 ,
а
,
а
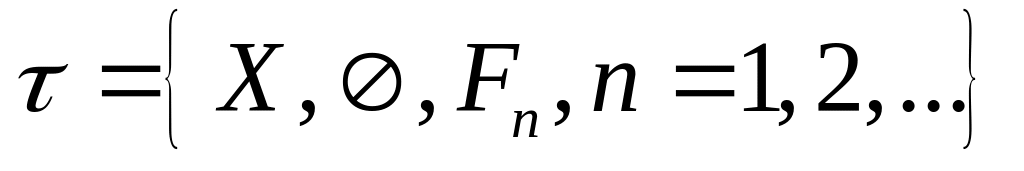 ,
где
,
где
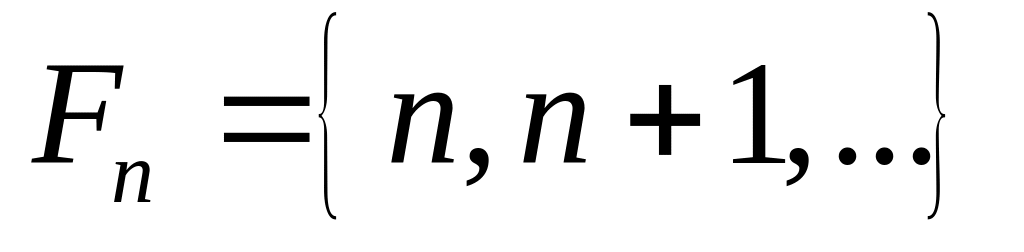 .
.
1) Будет ли компактным пространством?
2)
Найдите предел последовательности
![]() .
.
Что можно сказать о сходимости последовательности
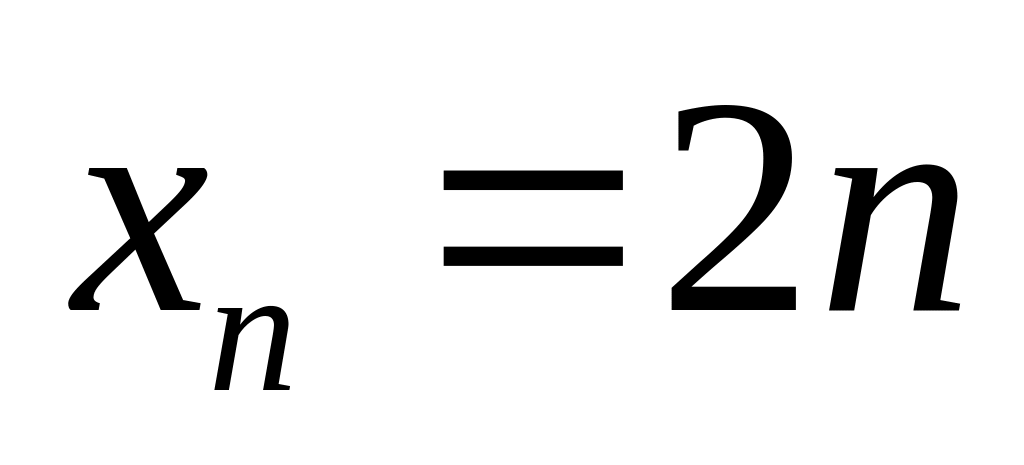 в топологическом пространстве
в топологическом пространстве
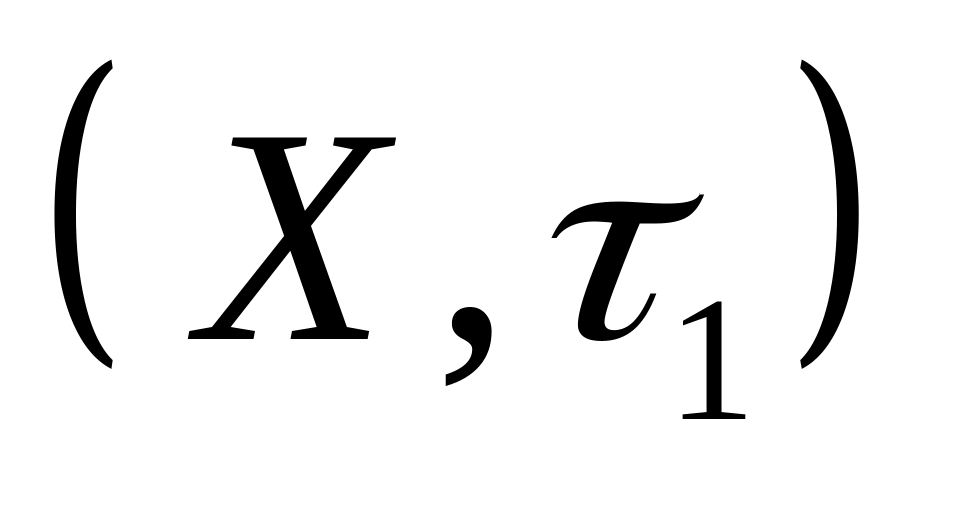 ,
если
,
,
если
,
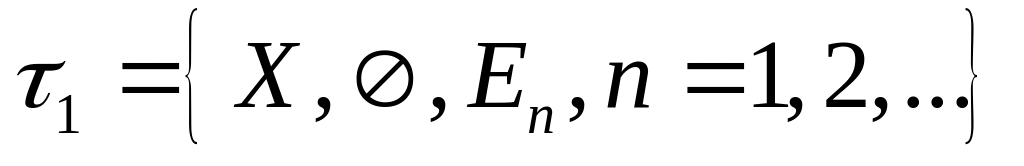 ,
где
,
где
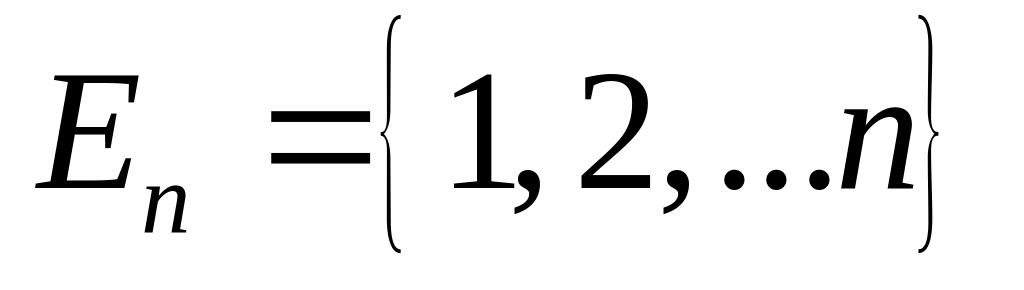 ?
Будет ли
компактным пространством?
?
Будет ли
компактным пространством?Пусть
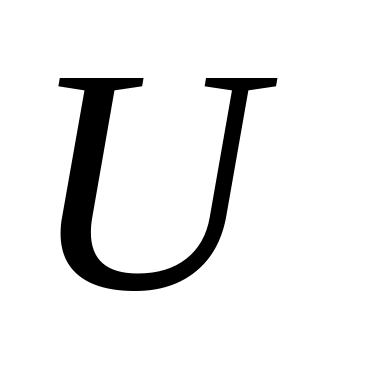 открыто,
открыто,
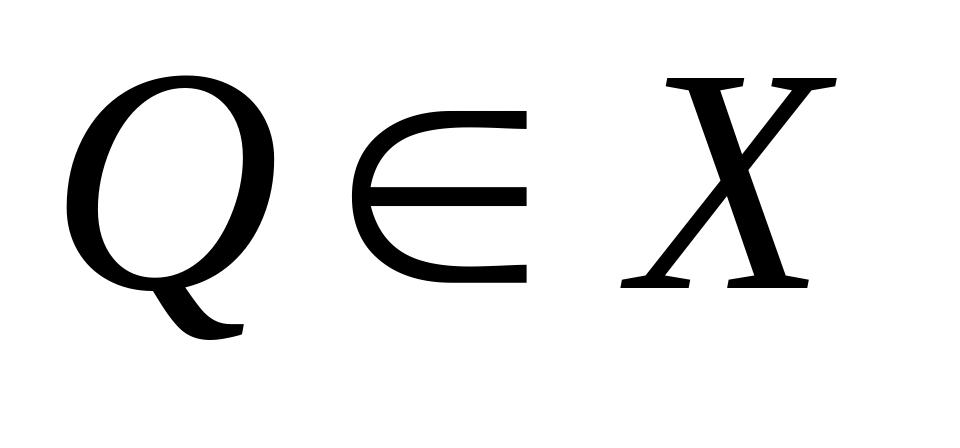 ,
где
,
где
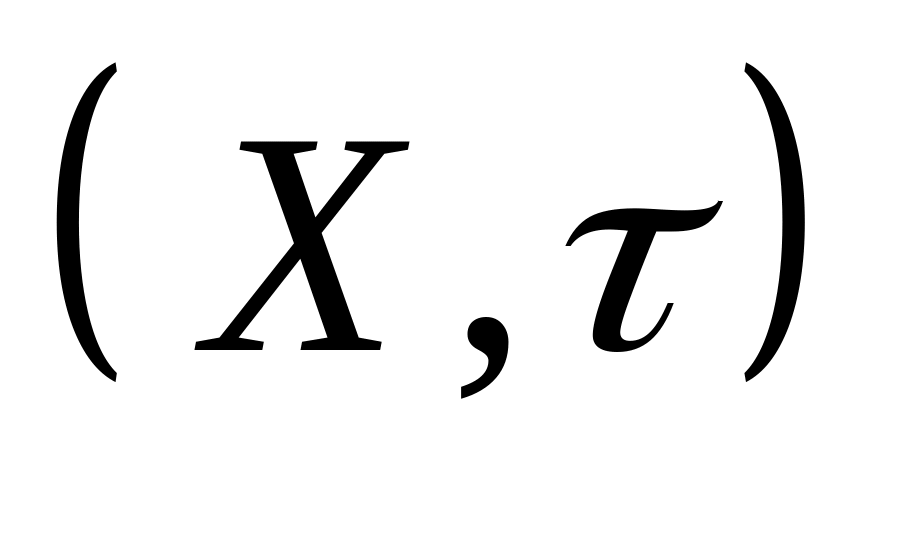 топологическое пространство. Доказать,
что
пересекается
с
топологическое пространство. Доказать,
что
пересекается
с
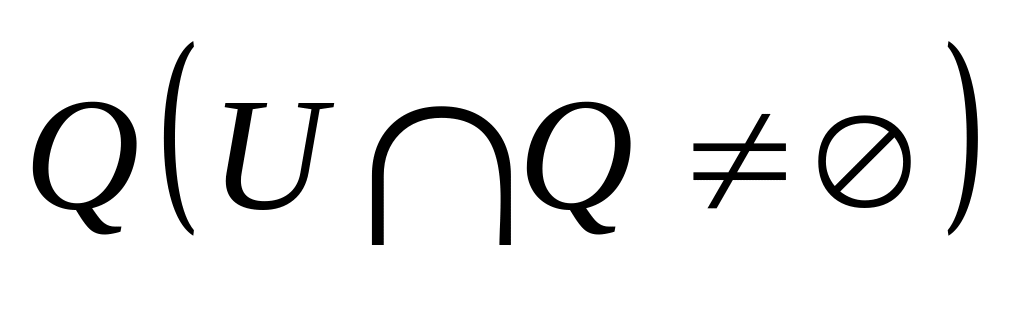 тогда и только тогда, когда
пересекается с замыканием
тогда и только тогда, когда
пересекается с замыканием
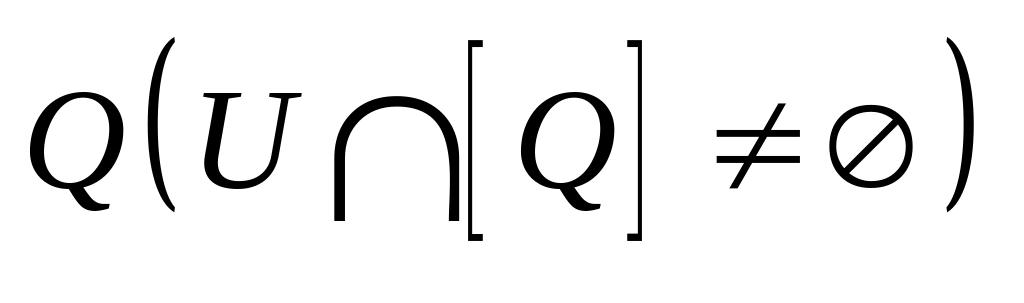 .
.Пусть
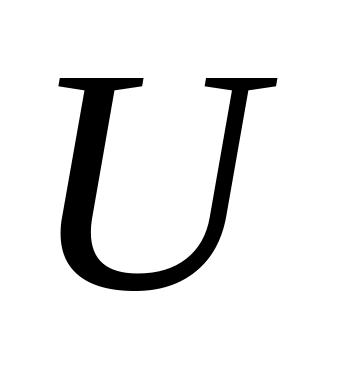 открыто,
открыто,
 ,
где
,
где
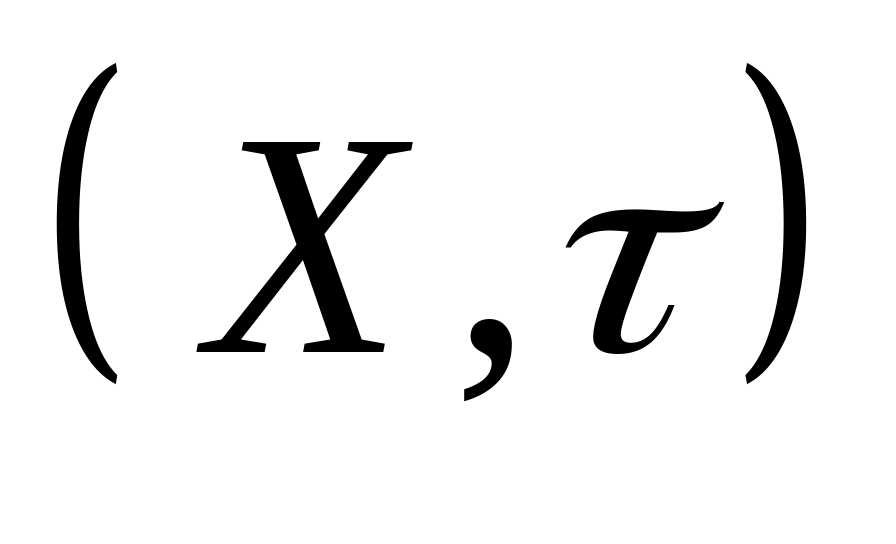 топологическое пространство. Доказать,
что
не пересекается с
топологическое пространство. Доказать,
что
не пересекается с
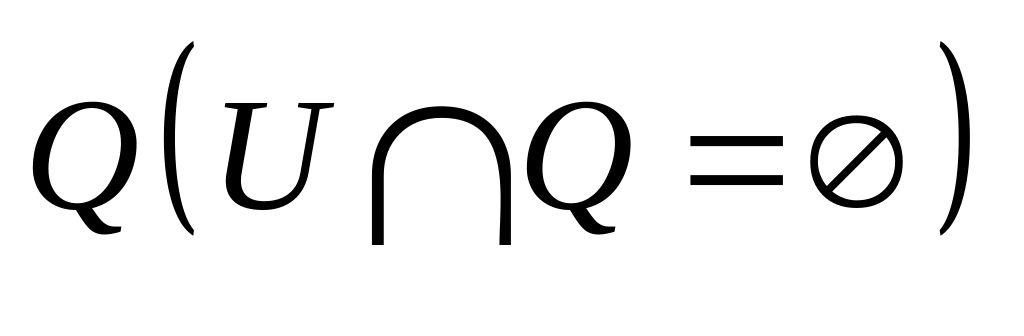 тогда и только тогда, когда
не пересекается с замыканием
тогда и только тогда, когда
не пересекается с замыканием
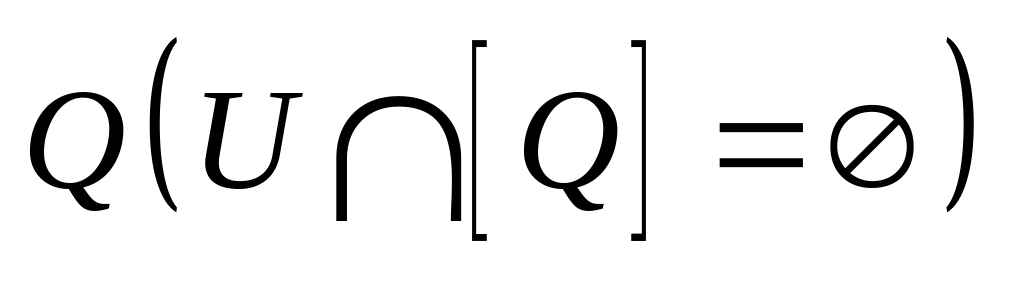 .
.Доказать, что в топологическом пространстве, если – открыто,
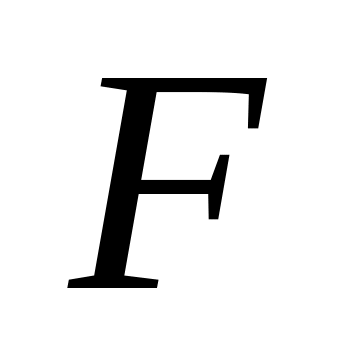 – замкнуто, то
– замкнуто, то
 – открыто, а
– открыто, а
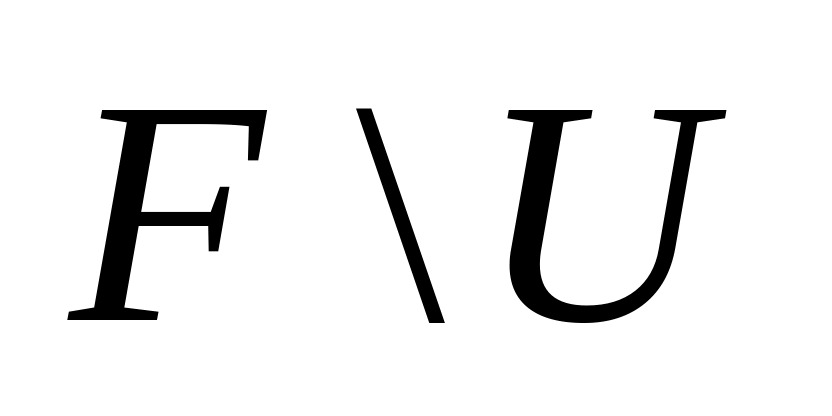 – замкнуто.
– замкнуто.Доказать, что если и
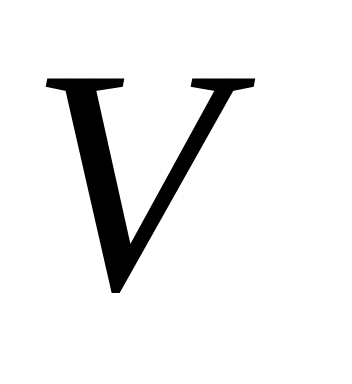 – открытые непересекающиеся множества
топологического пространства, то их
внутренности замыканий не пересекаются
– открытые непересекающиеся множества
топологического пространства, то их
внутренности замыканий не пересекаются
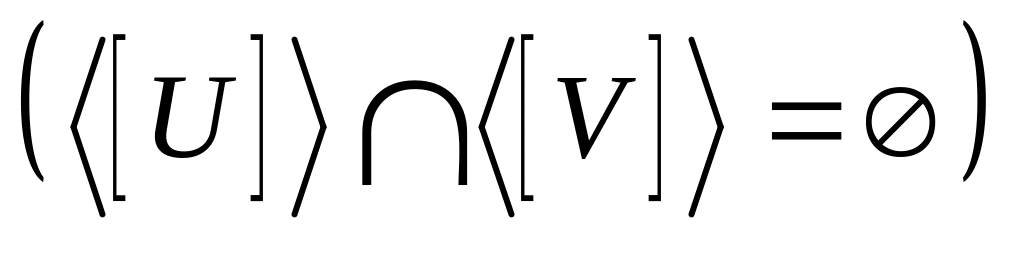 .
.Доказать, что если
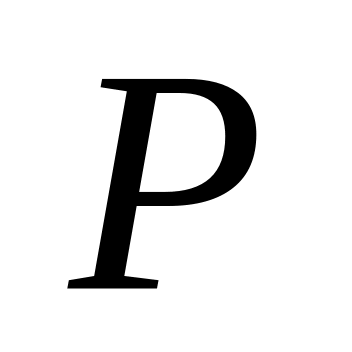 открыто в топологическом пространстве
открыто в топологическом пространстве
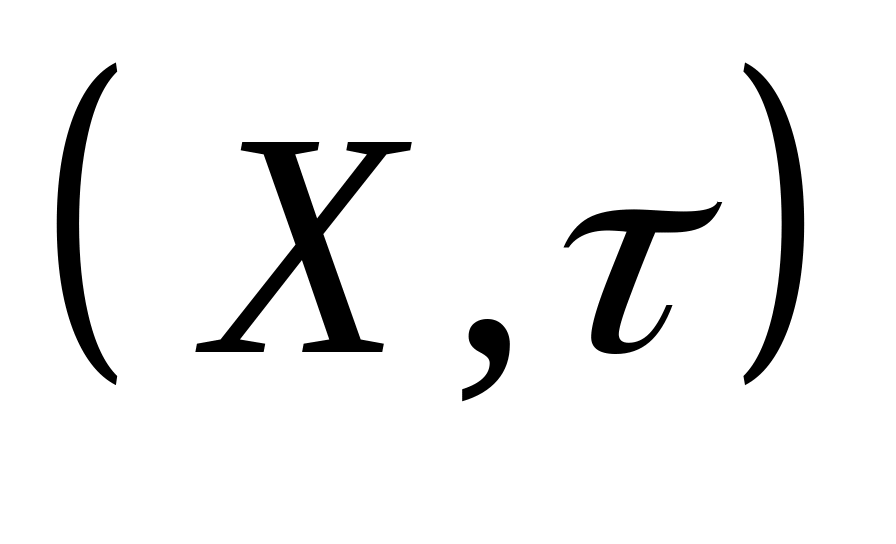 ,
,
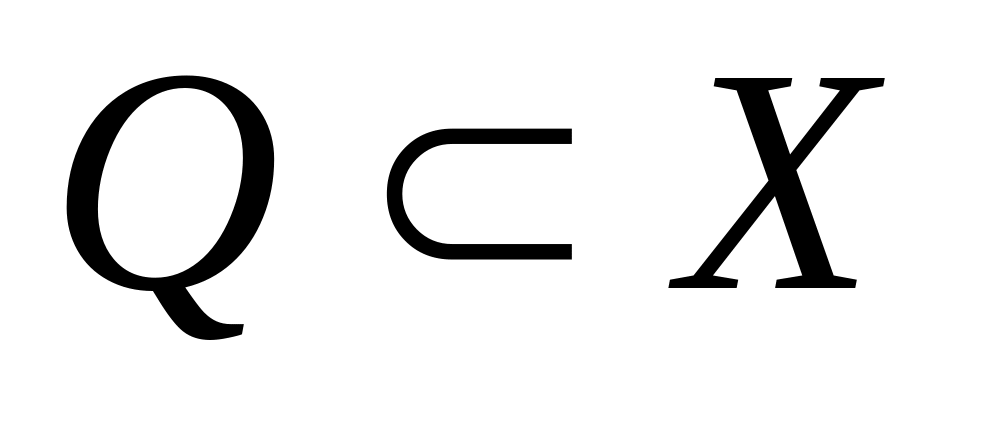 ,
то внутренность замыкания пересечения
множеств
и
,
то внутренность замыкания пересечения
множеств
и
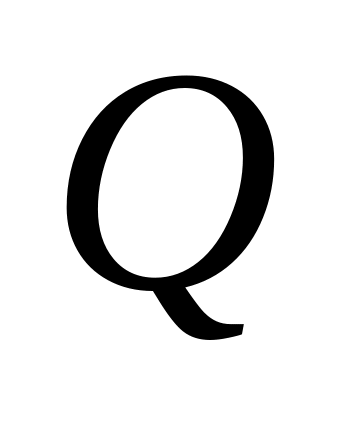 равна пересечению внутренностей их
замыкания
равна пересечению внутренностей их
замыкания
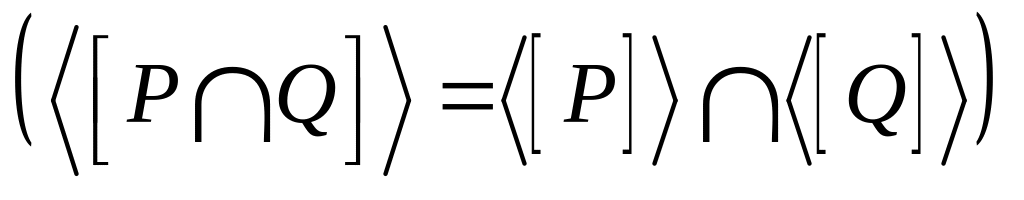 .
.Верно ли, что если – открыто в топологическом пространстве , то внутренность замыкания множества есть само
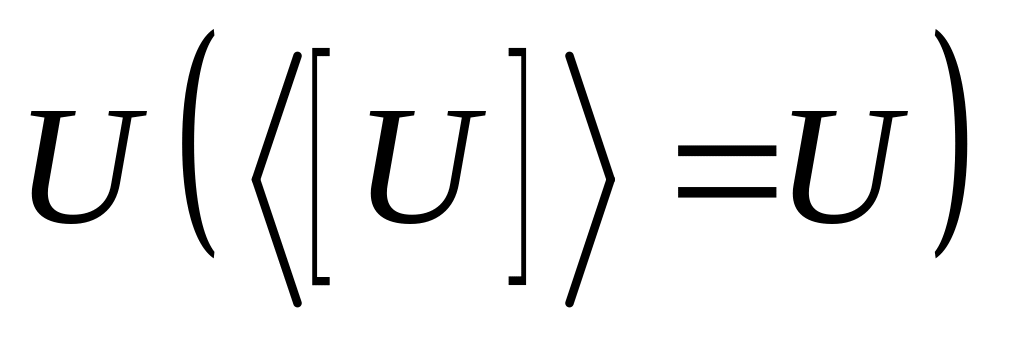 ?
?Верно ли, что если – замкнуто в топологическом пространстве , то замыкание внутренности множества есть само
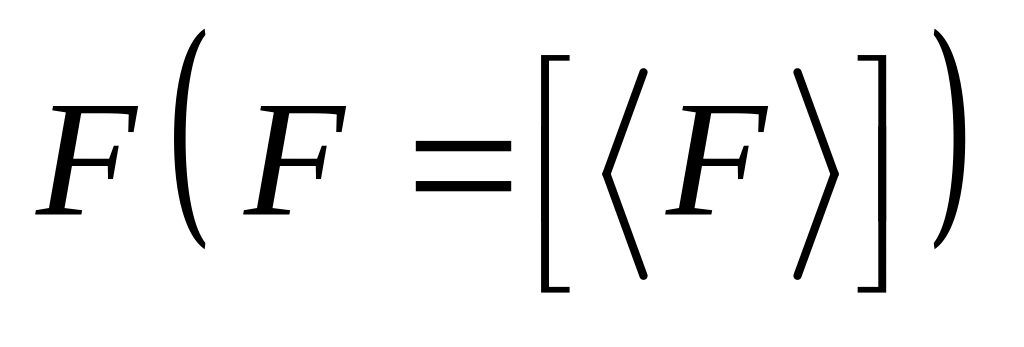 ?
?Верно ли, что в топологическом пространстве пересечение замыканий любых двух множеств равно замыканию их пересечения
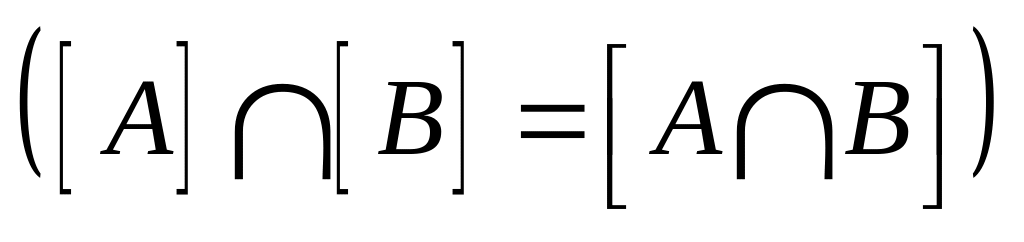 ?
?Верно ли, что в топологическом пространстве объединение внутренностей любых двух множеств равно внутренности их объединения
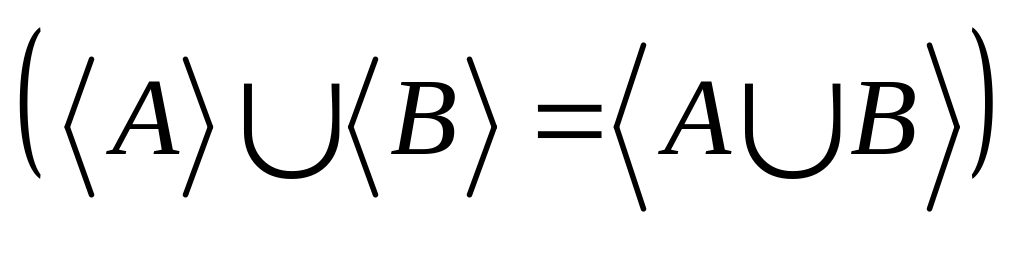 ?
?Пусть – топологическое пространство. Доказать, что:
если
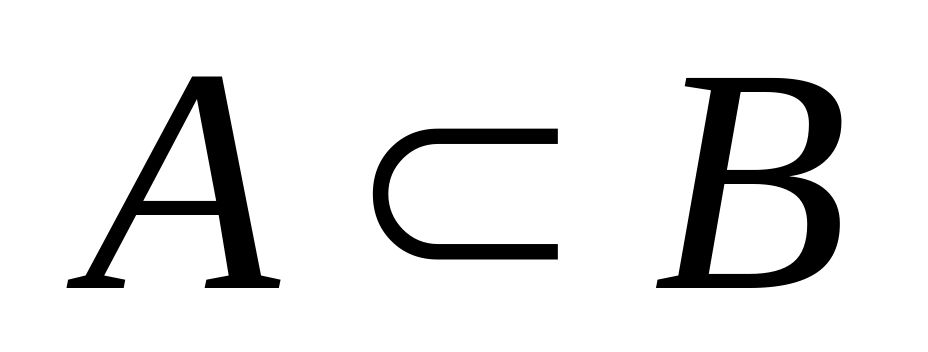 ,
то замыкание
содержится в замыкании
,
то замыкание
содержится в замыкании
 ;
;замыкание объединения любых двух множеств равно объединению их замыканий
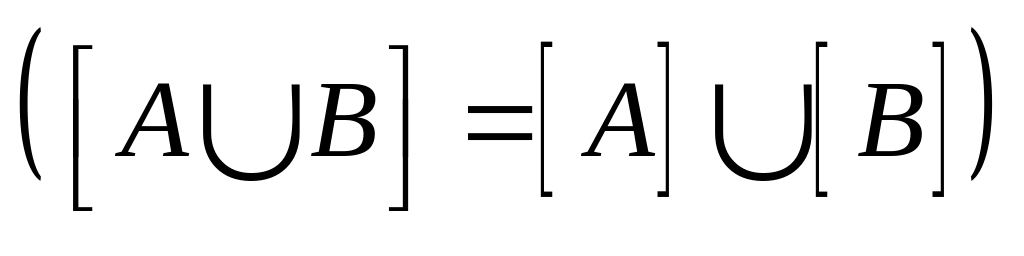 .
.
Пусть – топологическое пространство. Доказать, что:
если , то внутренность содержится во внутренности
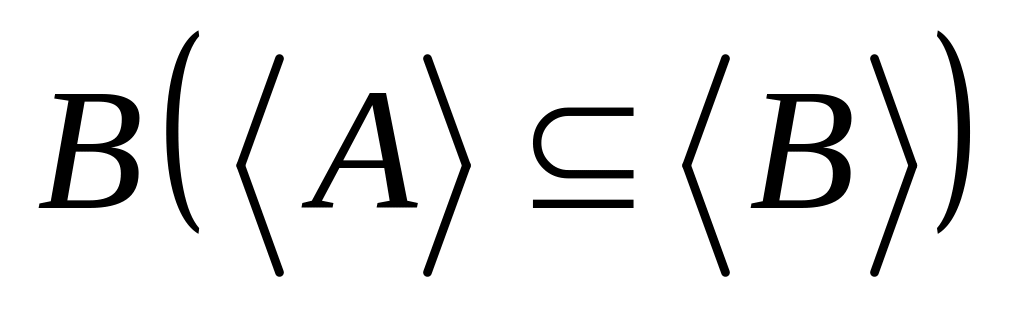 ;
;пересечение внутренностей любых двух множеств равно внутренности их пересечения
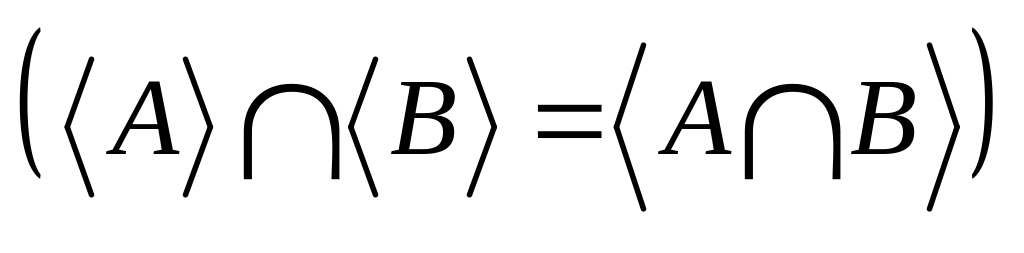 .
.
Доказать, что является
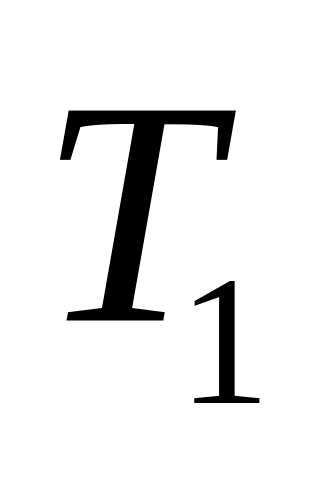 – пространством тогда и только тогда,
когда всякое его одноточечное подмножество
замкнуто.
– пространством тогда и только тогда,
когда всякое его одноточечное подмножество
замкнуто.Доказать, что для любых двух непересекающихся открытых множеств топологического пространства, замыкание любого из них не пересекается с другим.
