Вопрос 12

Поле -коммутативное кольцо, которое обладает свойствами группы и по умножению для не нулевых элементов.

Ноль- единичный элемент по сложению.

Единица- единичный элемент по умножению

(из лекции)

(из книжки)

Вопрос 14

Решетка

Пусть М -частично упорядоченное множество

<М,<= >

Для пар элементов а и b определены верхние и средняя границы

с =inf{c’, c’e M, c’<=a, c’<=b}

d = sup {d”:d”eM:a<=d”,b<=d”}

для конечных множеств супремум (sup)-это кол-ый максимум ;

инфинум ( inf) - это количественное минимальное число

с=a ∩ b опереция взятия минимума ( inf)

d= a ᴗ b операция взятия максимума (sup)

(из лекции)

(из книжки)

Решётка может быть также определена как универсальная алгебра с двумя бинарными операциями (они обозначаются + и ∙ или   и  ), удовлетворяющая следующим тождествам

1. a + a = a 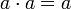 (идемпотентность)

2. a + b = b + a 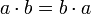 (коммутативность)

3. (a + b) + c = a + (b + c) 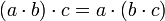 (ассоциативность)

4.  (поглощение).

Связь между этими двумя определениями устанавливается при помощи формул:

a + b = sup(a,b),  ,

и обратно. При этом для любых элементов a и b эквивалентны следующие утверждения:

;

ab = a;

a + b = b.

Понятия изоморфизма решёток как универсальных алгебр и как частично упорядоченных множеств совпадают. Однако произвольное изотонное отображение решётки R в решётку R' не обязано быть гомоморфизмом этих решёток как универсальных алгебр.

Примеры:

1. множество всех подмножеств данного множества, упорядоченное по включению;

2. всякое линейно упорядоченное множество; причём если  , то  ;

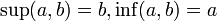3. множество всех подпространств векторного пространства, упорядоченных по включению, где 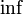  — пересечение, а   — сумма соответствующих подпространств;

4. множество всех неотрицательных целых чисел, упорядоченных по делимости:  , если b = ac для некоторого c. Здесь   — наименьшее общее кратное, а   — наибольший общий делитель данных чисел;

5. вещественные функции, определённые на отрезке [0, 1], упорядоченные условием 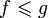 , если 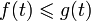  для всех 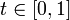 . Здесь

, где u(t) = max(f(t),g(t)).

(интернет)

Не все примеры не нашла. Если так и не найду, отсканирую в лекциях пример где мы разбирали все свойства.

16. Запишите определение основных операций алгебры логики. Дать определение функции алгебры логики.

Алгебра логики - раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними (из интернета).

Алгебра, образованная множеством В вместе со всеми возможными операциями на нем, называется алгеброй логики. Элементы данного множества часто обозначают 0 и 1, т.е. В={0, 1}. Наиболее распространенная интерпретация двоичных переменных – логическая: «да» - «нет», «истинно» (И) – «ложно» (Л).

Функцией алгебры логики (или логической функцией) от n переменных называется n – арная операция на B.

Итак, логическая функция f (x₁, …, x_n) – это функция, принимающая значения 0, 1. Множество всех логических функций обозначается P₂, множество всех логических функций n переменных – P₂(n).

Основные логические операции алгебры логики:

• Логическое отрицание (инверсия) (НЕ) – это логическая операция, применяемая к одному высказыванию. Высказывание А есть высказывание, которое ложно, когда А истинно, и истинно, когда А ложно. Высказывание называется отрицанием А.

Обозначение: ^¬А

• Логическое умножение (конъюнкция) (И) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Обозначение: А&В

• Логическое сложение (дизъюнкция) (ИЛИ) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда истинно хотя бы одно из высказываний. Обозначение: А˅В

• Логическое следование (импликация) – это высказывание ложно тогда и только тогда, когда А истинно, а В ложно. Обозначение: А→В

• Эквивалентность – это высказывание истинно тогда и только тогда, когда А и В оба истинны или оба ложны. Обозначение: А↔В