
- •Вопрос 1.
- •Вопрос 2 Бинарные отношения на множестве
- •Вопрос 3-4
- •Вопрос 5:
- •Вопрос 1.
- •Вопрос 2 Бинарные отношения на множестве
- •Вопрос 3-4
- •Вопрос 5:
- •Вопрос 10
- •Вопрос 11
- •Вопрос 12
- •Вопрос 14
- •16. Запишите определение основных операций алгебры логики. Дать определение функции алгебры логики.
- •17. Как задать функцию алгебры логики в виде таблицы истинности и формулы? Сколько существует логических функций от n переменных?
- •18. Опишите понятие «булева алгебра логических функций». Опишите правила основные свойства операций, представленных в булевой алгебре. Примените эти правила для упрощения формул.
- •19. Дайте определения сднф и скнф. Как построить такие представления для произвольной логической функции, заданной таблицей истинности или формулой?
- •20. Какие функции называются монотонными, линейными, самодвойственными, сохраняющими ноль и сохраняющими единицу? Приведите примеры таких функций. Докажите замкнутость классов таких функций. Вопрос 27
- •Вопрос 28
- •Вопрос 29
- •Вопрос 30
- •Вопрос 31
- •32)Дать определение графа и основных его видов:ориентированный и неориентированный,мультиграф,взвешенный граф,граф с петлями,планарный граф
- •33) Описать основные способы задания графов:матрица смежности,матрица инцидентности,список смежности.Степени вершин графа.Теоремы о свойствах степени вершин.
- •34)Что называется маршрутом в графе? Основные виды маршрутов : определения и примеры. Нахождение кратчайших маршрутов.
- •35)Дать определение эйлеровых циклов и цепей,условия их существования в графе.Описать построения эйлерова цикла.
- •36)Дать определиние гамильтонова цикла и цепи.
Вопрос 3-4
Пример 1
N-множество натуральных чисел
Отношение “≤” на множествах N и D рефлексивно, а отношение “<” антирефлексивно. N
Бинарное отношение называется симметричным, если (x,y) ∈R⇒(y,x) ∈R. То есть для любой пары отношение выполняется в обе стороны либо не выполняется вообще. Матрица симметричного отношения симметрична относительно главной диагонали.
Отношение R называется антисимметричным, если из (x, y) ∈R и (y,x) ∈R следует x = y.
Пример 2
1. Отношение “∩” является симметричным.
Отношение “≤” является антисимметричным.
Бинарное отношение называется транзитивным, если (x,y) ∈ R и (y,z) ∈ R, ⇒ (x, z),∈R .
Пример 3
1. Отношение “=” на D является транзитивным: .x=y и y=z ⇒ x=z
2. Отношение “≤” на является транзитивным.
3. Отношение включения для множеств транзитивно: . A⊆B и B⊆C⇒A⊆C
4. Отношение “∩” не транзитивно: из A∩B≠∅ и B∩C≠∅ не следует A∩C≠∅.
Бинарное отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.
Пример 4
1. Отношение равенства на D есть отношение эквивалентности.
3. Отношение “иметь один и тот же остаток от деления на какое-либо число” является эквивалентностью на N
Вопрос 5:
Рефлексивное, транзитивное и асимметричное отношение на множестве А называется частичным порядком на .
Такие бинарные отношения часто обозначаются символом “≤”. Тогда аксиомы частичного порядка можно записать в виде:
1) x≤x для всех – рефлексивность x ∈A;
2) из x≤y и y≤z следует x = y – антисимметричность;
3) из x≤y и y≤z следует x≤z – транзитивность.
Пример 6
1. Обычное отношение “≤” на множествах N и D является частичным порядком.
2. Отношение делимости на N.
Для любого множества отношение “⊆” является частичным порядком на множестве всех подмножеств U.
Отношение, обратное к частичному порядку “≤”, является частичным порядком, который называется двойственным к “≤” и обозначается “≥”. Таким образом x ≥y, , тогда и только тогда, когда y ≤x Если и x ≤y и x ≠ y, то используется обозначение x <y.
Бинарное отношение на называется отношением нестрогого частичного порядка (или нестрогим порядком) на , если оно транзитивно, антисимметрично и рефлексивно, то есть
Вопрос 10

(из книжки)
Непустое
множество G с
заданной на нём бинарной
операцией ![]() называется
группой (G,
* ),
если выполнены следующие аксиомы:
называется
группой (G,
* ),
если выполнены следующие аксиомы:
ассоциативность:
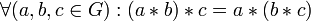 ;
;наличие нейтрального элемента:
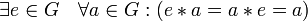 ;
;наличие обратного элемента:

(интернет)
Вопрос 11

(из книжки)
Кольцо
K=<M;x;+>
-k-коммутативная группа по сложению
-умножение является ассоциативным
- +> дистрибутивность
a * (c+b)=a*b+a*c
(из лекции)
Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:
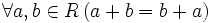 — коммутативность сложения;
— коммутативность сложения; — ассоциативность сложения;
— ассоциативность сложения; —
существование
нейтрального элемента относительно
сложения;
—
существование
нейтрального элемента относительно
сложения;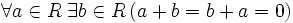 —
существование обратного
элемента относительно
сложения;
—
существование обратного
элемента относительно
сложения; —
ассоциативность
умножения (некоторые авторы не требуют
выполнения этой аксиомы[1])
—
ассоциативность
умножения (некоторые авторы не требуют
выполнения этой аксиомы[1])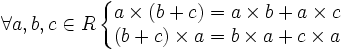 — дистрибутивность.
— дистрибутивность.
Иными
словами, кольцо —
это универсальная
алгебра ![]() ,
такая что алгебра
,
такая что алгебра ![]() — абелева
группа,
алгебра
— абелева
группа,
алгебра ![]() — полугруппа и
операция + дистрибутивна слева
и справа относительно
— полугруппа и
операция + дистрибутивна слева
и справа относительно ![]() .
Кольцо ассоциативно, если мультипликативный
группоид является полугруппой.
.
Кольцо ассоциативно, если мультипликативный
группоид является полугруппой.
Ассоциативные кольца могут обладать следующими дополнительными свойствами:
наличие единицы:
 (кольцо
с единицей);
(кольцо
с единицей);коммутативность умножения:
 (коммутативное
кольцо);
(коммутативное
кольцо);отсутствие делителей нуля:
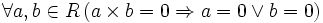 .
.
Кольца, для которых выполнены все вышеперечисленные условия, называются целостными (иногда также областями целостности или просто областями, хотя условие коммутативности не всегда считается обязательным).
Иногда под ассоциативным кольцом понимают ассоциативное кольцо с единицей. Но имеются примеры ассоциативных колец без единицы, например — нулевое кольцо, кольцо чётных чисел, или же любой несобственный идеал в кольце. Рассматриваются также неассоциативные кольца без единицы, например лиевские кольца и др.
(интернет)
