
- •Вопросы для самопроверки по дисциплине «Математика (Модуль 1)»
- •Чётность
- •Уравнение пучка прямых Уравнение прямой в отрезках
- •Общее уравнение прямой и его исследование
- •Предел числовой последовательности
- •Предел функции в бесконечности и в точке
- •Признаки существования предела
- •Свойства бесконечно малых
Признаки существования предела
Теорема 1. Если числовая последовательность монотонна и ограничена, то она имеет предел.
Теорема
2. Если в некоторой окрестности точки
![]() (или
при достаточно больших значениях
)
функция
(или
при достаточно больших значениях
)
функция
![]() заключена
между двумя функциями
заключена
между двумя функциями
![]() и
и
![]() ,
имеющими одинаковый предел
при
,
имеющими одинаковый предел
при![]() (или
),
то функция
имеет
тот же предел
.
(или
),
то функция
имеет
тот же предел
.
Пусть
при
![]() ,
,
![]() .
.
Это
означает, что для любого
![]() найдется
такое число
найдется
такое число
![]() ,
что для всех
,
что для всех
![]() и
удовлетворяющих условию
и
удовлетворяющих условию
![]() будут
верны одновременно неравенства:
будут
верны одновременно неравенства:
![]() (1.1)
(1.1)
или
![]()
Т.к. по условию функция заключена между двумя функциями, т.е.:
![]() ,
то из неравенств (1.1) следует, что
,
то из неравенств (1.1) следует, что
![]() ,
т.е.:
,
т.е.:
![]() .
.
А это
и означает, что
![]()
13. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать).
Предел функции в точке: Пусть функция задана в некоторой окрестности точки , кроме, быть может, самой точки .
Определение.
Число
называется
пределом функции
![]() при
стремящемся
к
(или
в точке
),
если для любого, даже сколько угодно
малого положительного числа
,
найдется такое положительное число
при
стремящемся
к
(или
в точке
),
если для любого, даже сколько угодно
малого положительного числа
,
найдется такое положительное число
![]() (зависящее
от
),
что для всех
,
не равных
и
удовлетворяющих условию
,
выполняется неравенство
(зависящее
от
),
что для всех
,
не равных
и
удовлетворяющих условию
,
выполняется неравенство
![]() .
.
Это
предел функции обозначается:
![]() или
при
или
при
![]() .
.
Если
при стремлении
к
переменная
принимает
лишь значения, меньшие
,
или наоборот, лишь значения большие
,
и при этом функция
стремится
к некоторому числу
,
то говорят об односторонних пределах
функции
соответственно
слева
![]() и
справа
и
справа
![]()
1. Предел константы равен самой этой константе:
![]() с
= с.
с
= с.
2. Постоянный множитель можно выносить за знак предела:
[ k • f (х)] = k • f (х).
3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций:
[ f (х) ± g (х)] = f (х) ± g (x).
4. Предел произведения функций равен произведению пределов этих функций:
[ f (х) • g (х)] = f (х) • g (x).
5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:
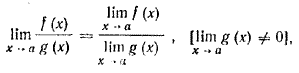
14. Бесконечно малые величины (определение). Свойства бесконечно малых (одно из них доказать). Бесконечно большие величины, их связь с бесконечно малыми.
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Свойства бесконечно малых
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если an — бесконечно малая последовательность, сохраняющая знак, то
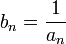 — бесконечно
большая последовательность.
— бесконечно
большая последовательность.
Связь бесконечно больших и бесконечно малых величин устанавливает следующая теорема.
Теорема
2.16
Пусть
![]() --
функция, бесконечно большая при базе
--
функция, бесконечно большая при базе
![]() .
Тогда величина
.
Тогда величина
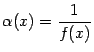 --
бесконечно малая при базе
.
--
бесконечно малая при базе
.
Доказательство.
Для начала заметим, что на всех достаточно
далёких окончаниях
![]() базы
будет
базы
будет
![]() ,
так что функция
,
так что функция
![]() определена
на этих окончаниях. Далее, пусть взято
некоторое
определена
на этих окончаниях. Далее, пусть взято
некоторое
![]() .
Положим
.
Положим
 и
выберем такое окончание
,
что
и
выберем такое окончание
,
что
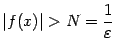 при
при
![]() из
этого окончания. Тогда
из
этого окончания. Тогда
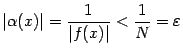 при
таких
,
что и означает, что
при
таких
,
что и означает, что
![]() .
.
Замечание
2.9
Утверждение, обратное к доказанной
теореме, вообще говоря, неверно: если
--
бесконечно малая при базе
,
то функция
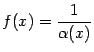 не
всегда является бесконечно большой при
базе
,
хотя бы потому, что может быть не
определена ни на каком окончании
базы
.
Простейший пример -- это постоянная
величина
не
всегда является бесконечно большой при
базе
,
хотя бы потому, что может быть не
определена ни на каком окончании
базы
.
Простейший пример -- это постоянная
величина
![]() ,
которая, очевидно, бесконечно мала при
любой базе (
,
которая, очевидно, бесконечно мала при
любой базе (
![]() ),
но
),
но
![]() не
имеет смысла ни при каких
.
Однако если сделать дополнительное
предположение, что
не
имеет смысла ни при каких
.
Однако если сделать дополнительное
предположение, что
![]() при
всех
из
некоторого окончания
базы
,
то обратное утверждение становится
верным.
при
всех
из
некоторого окончания
базы
,
то обратное утверждение становится
верным.
15. Второй замечательный предел, число е. Понятие о натуральных логарифмах.
16. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры.
17. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке.
18. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему).
19. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
20. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции.
21. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.
22. Достаточные признаки монотонности функции (один из них доказать).
23. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).
24. Достаточные признаки существования экстремума (доказать одну из теорем).
25. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры.
26. Общая схема исследования функций и построения их графиков. Пример.
27. Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия.
28. Понятие об эмпирических формулах и методе наименьших квадратов. Подбор параметров линейной функции (вывод системы нормальных уравнений).
29. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала 1-го порядка.
30. Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать).
31. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
32. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
33. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
34. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона–Лейбница.
34. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства).
35. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
