2. Знаходження коренів поліномів

Для знаходження коренів поліномів є вбудована функція polyroots(a). Аргументом функції є вектор коефіцієнтів полінома , тобто для рівняння вектор а має вигляд

Якщо в поліномі відсутні деякі члени, то на відповідних місцях замісто коефіцієнтів слід писати 0. Знайдемо корені полінома

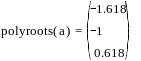_{Коефіцієнти полінома можуть бути і комплексними:}

3. Знаходження коренів системи лінійних рівнянь

Методы решения систем линейных уравнений можно разделить на две основные группы: прямые методы и итерационные. Прямые методы дают точное решение за конечное число операций; к ним относятся, например, методы Крамера и Гаусса. Итерационные методы дают решение системы уравнений как предел последовательных приближений.

3.1. Рішення системи лінійних рівнянь алгебри як матричне рівняння Ax=b:

1) Створюємо квадратну матрицю А коефіцієнтів при змінних у лівих частинах рівнянь.

2) Створюємо вектор-стовпчик В з вільних членів.

3) Знаходимо розв’язок системи як k = A^-1B.

4) Виконуємо перевірку знайдених коренів.

5) Знаходимо рішення системи за допомогою функції lsolve(A, B).

Приклад. Знайти корені системи рівнянь:

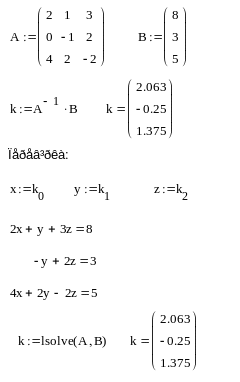
3.2. Рішення лінійної системи методом Гауса

Функція augment(A,b) формує розширену матрицю системи додаванням до матриці системи справа стовпця правих частин. Функція rref приводить розширену матрицю системи до ступінчастого вигляду, виконуючи прямий і зворотний ходи гауссова виключення. Останній стовпець містить рішення системи.

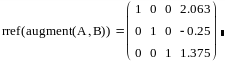
3.3. Решение системы методом Крамера

Порядок выполнения работы.

1. Вычисляем D определитель матрицы А.

2. Зададим матрицу DX1, заменой первого столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX1.

3. Зададим матрицу DX2, заменой второго столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX2.

4. Зададим матрицу DX3, заменой третьего столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX3.

5. О 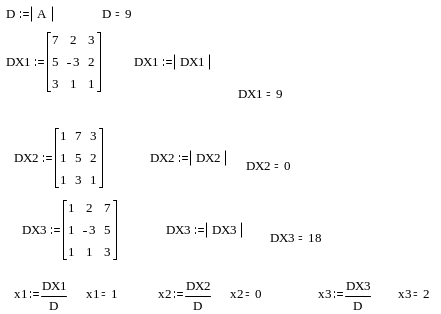пределяем решение системы линейных уравнений x_1, x₂, x₃.

3.4.Рішення системи лінійній алгебрі рівняння методом простих ітерацій

Порядок виконання завдання

1. Введіть матриці C і d.

2. Преобразуйте исходную систему Cx=d до вигляду x=b+Ax.

3. Визначте нульове наближення рішення.

4. Задайте кількість ітерацій.

5. Обчисліть послідовні наближення.

3.5. Рішення системи лінійних рівнянь алгебри методом Зейделя

Порядок виконання завдання

1. Введіть матриці С і d.

2. Перетворіть систему Cx=d до вигляду x=b+A1x+A2x.

1. Визначте нульове наближення рішення.

2. Задайте кількість ітерацій.

3. Обчисліть послідовні наближення.

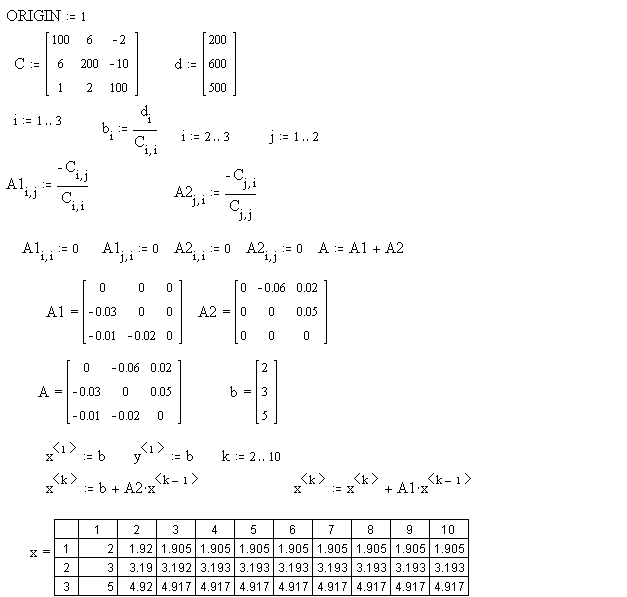
Початкові дані для розв’язку рівнянь і систем:

№ варіанта	Рівняння	Система лінійних рівнянь
1
2
3
4
5	(перші три корені)
6
7
8	(перші три корені)
9
10

Лабораторна робота №3