Соотношение между током и напряжением на элементах электрической цепи
Р езистор
Для амплитуд и действующих значений закон Ома справедлив.
На
резисторе фаза напряжения и тока
совпадает (синфазное напряжение и ток):
И
ндуктивность
– сопротивление индуктивности на
частоте 
:
Тогда закон Ома справедлив.
Ток
отстает от напряжениния на 
(по фазе):
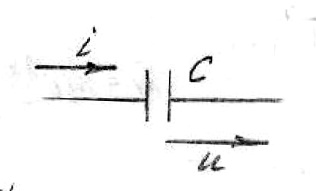
Емкостть
=
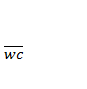
Зако Ома справедлив.
Напряжение отстает от тока по фазе на :
В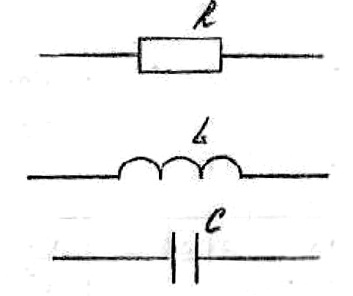
ывод:
; 
; 
Если в цепи действууют гармонические источники одной чистоты, то все токи и напряжения также будут гармоническими функциями с той же частотой (для линейных цепей)
Символьный метод расчета. (Метод комплексных амплитуд).
О
бозначения:
m,
Например:
; 
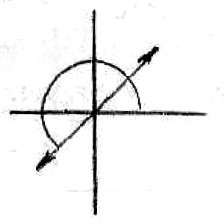
Векторное представление гармонической функции
Декартова система координат:
(Тригономическая форма)
Полярная
система коорд инат : 
(показательная форма)
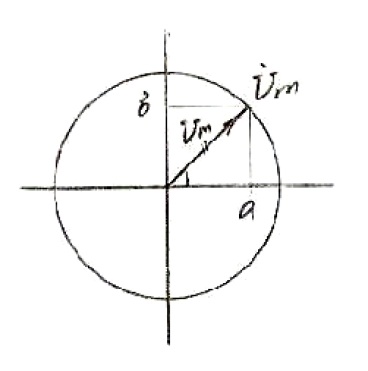
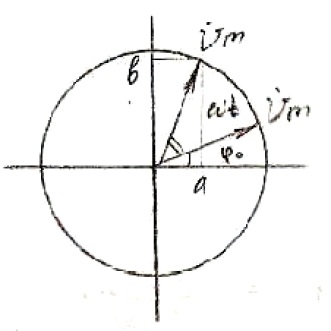
cos:
sin:
U (t) – мгновенное значение напряжения, пропорция времени
- комплексное мгновенное значение
напряжения, вращающийся вектор.
Vm - амплитуда напряжений; неподвижный вектор.
V - действующее значение напряжения; скаляр.
-
оператор вращения.
; 
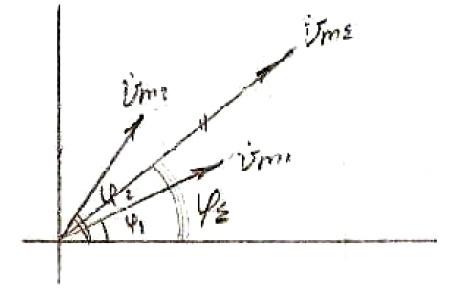
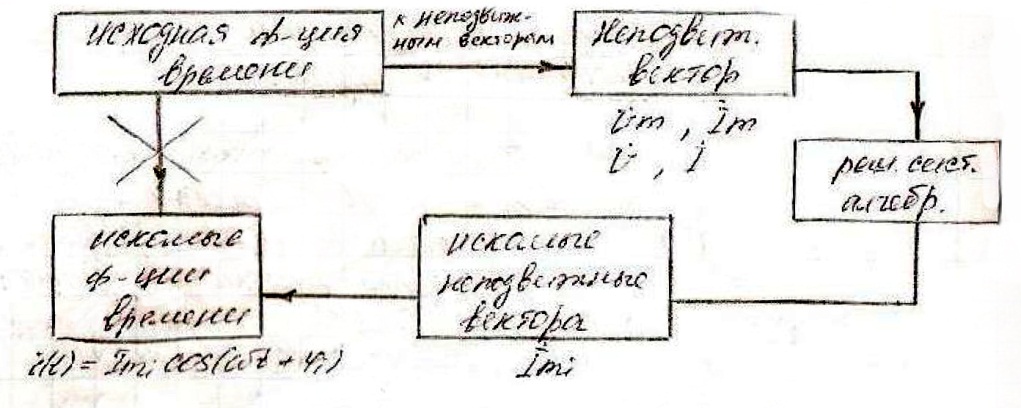
Переход от функциии времени к комплексным амплитудам называют алгебродезацией.
Некоторые операции с комплексными числами
Декартова система координат: Полярная система координат:
X=a+jb
y=c+jd
1) 2=x+y
Z
=x+y=a+jb+c+jd=
=(a+c) + j(b+d)
Rl123 Jm123
2
)
E=x+y
2=(a+jb)-(c+jd)=
=(a-c) + j(b-a)
Rl (2) Jm 123
3) 2=x-y