• Искомый объем продукции первого вида

• объём продукции второго вида

Цель максимум прибыли.

1 руб.* X1 – прибыль от реализации 1 вида продукции

2 руб.* X2 - прибыль от реализации 2 вида продукции

Целевая функция

Обозначим в целевой функции коэффициенты при переменных через С1 и С2, тогда целевая функция будет иметь вид:

В ведем систему ограничений, которая характеризует использование оборудования. Планирование использования машин по цехам не должен превышать наличие этого оборудования по цеху А (из таблицы).

- Ограничение первое по цеху А

- Ограничение второе по цеху Б

• Ограничение третье по цеху В

- Общие ограничения

Решение задачи возможно двумя методами графоаналитическим и симплексным.

2 . Представим решение задачи графоаналитическим методом. С этой целью используем изложенные выше правила и построим координатную плоскость.

9

8 (1)

7

6

5

4 А В (3)

3

2 С

1 (2)

О 1 2 3 4 5 6 7 8 9 10 11 Д 12 13 14 15 16

Фигура получилась от пересечения линейных форм. Многоугольник определяет ОДР, с целью нахождения вершины (значения наилучшей альтернативы). Введем дополнительный уровень, произвольно, находящийся в ОДР.

К графическому методу решения задачи выбора из совокупности альтернатив наилучшей, всегда можно свести к решению двухмерной задачи графическим способом.

А налитический способ нахождения координаты точки С., используется при отсутствии необходимости графического представления оптимального решения. В этом способе система уравнений (применимо к ранее формулированной задачи) будет иметь вид:

Поставим полученные решения в уравнение 2, имеем

получим:

X2=2

9+3Х2 = 15

Задача оптимизации доходов.

Завод изготавливает детали для автомобиля. Выпуск второго типа деталей (X1,X2). Завод располагает фондом рабочего времени 4000 ч/ч в неделю. Для производства одной детали типа X1 требуется 1 ч/ч, и для X2 2ч/ч. Производственная мощность завода позволяет выпускать X=2250 и X=1550 деталей в неделю. Каждая деталь типа X2 требуют 2 кг металлических стержней, и 5 кг листового метала. Для производства X1 (1 деталь) необходимо 5 кг стержней и 2 кг листового металла. Уровень запаса каждого вида металла составляет 10000кг. Ежедневно завод поставляет 600 деталей 1 вида своему заказчику. Существует также профсоюзное соглашение в соответствие, с которым общее число производимых в неделю деталей составляет не менее 1500штук.

Требуется определить сколько деталей каждого типа нужно производить, чтобы максимизировать общий доход за неделю, если доход за неделю X1=30 у.е., X2=40 у.е.?

Критерий максимум доход, целевая функция имеет вид:

Ф

- План производства 1 детали (объем производства)

- План производства 2 детали

ормализация задачи: пусть переменная

Т огда целевая функция будет иметь вид:

в ведем ограничения:

1. ограничение по фонду рабочего времени, планированное рабочее время не должно иметь ограничение

2. по производственной мощности

3. по уровню запасов, планированное использование материалов каждого вида не должно превышать 10000 кг

4. по обязательствам поставки первых деталей

5. по профсоюзному ограничению

6. условие не отрицательности

Решение:

С троим систему координат, при фиксированном времени.

7

6

5

4

(2)

3

2 С д

1 Д

1 2 3 4 5 6 7 8

Построение областей ограничения

Строим целевую функцию (произвольно)

Оптимальная точка определения плана производства достигается максимальным доходом.

Это точка Д (1500, 1250)

Аналитический способ:

Резюме

Рассмотренный выше задачи оптимизации планирования производства по критерию максимум прибыли и дохода, при решения графическим или аналитическим методом, в случаи небольшой размерности переменных наглядны и точны в своих решениях.

Линейное программирование методом потенциалов

в транспортных задачах.

В транспортных задачах обычно имеется база А располагающих каким-либо количеством машин n и объекты (потребители) Б нуждающихся в этих машинах, количество потребляемых машин объектами Б (m).

Машины объектам Б нужны для выполнения запланированного объема работ.

База А и объекты Б заинтересованы в обеспечении min простоя машин которые зависят от плана распределения их по базам и объектам. В ЛП потенциалами являются некоторые числа U_Ai и U_Бj соответственно к базам и объектам. Сумма которых для клеток табличного плана содержащих цифры распределенных машин, применяется равным результатов времени простоев:

U_Аi+U_Бj=C_ij (12.1)

Там где в клетках табличного плана нет распределения машин по объектам эта сумма будет не более стоимости результатов (Cij*Хij)

UАi+UБj (Cij*Хij) (12.2)

План распределения машин по объектам отображенный в таблице планов всей клетки которого отвечают условиям 12.1, 12.2 являются оптимальными.

Задача: транспортная и РУР для ее решения.

Описание реального объекта.

Пусть имеются предприятия занимающихся механизацией трудоемких работ и располагает набором однородных технических средств в количестве n=30 еденицам. Машины размещаются на 3х базах Реутово (А1), Железнодорожный, (А2) Балашиха, (А3) при этом базы А1и А2 имеют по 11 машин, а база А3 8ед. Использование этой техники планируется на 4х объектах Б1,Б2,Б3,Б4.

Объекты Б1 нуждаются в 5ед.

Б2 и Б3 нуждаются в 9ед.

Б4 нуждается в 7ед.

Эффективность эксплуатации max средств во многом зависит от того на сколько интенсивно они используются или не используются простаивают. При этом чем меньше время простоев, тем выше эффективность технических средств.

Под простоем здесь понимается количество свободного времени (Тij) в течение которого ТС базой Аi не используются объектом Бj. Общая характеристика использования ТС с указанием ее наличия и потребности на объектах и базах приведено в таблице 12.1

Базы	Кол-во ТС	Б1	Б2	Б3	Б4
А1	11	5	9	9	7
А2	11	7	8	5	3
А3	11	2	4	5	9
Uвj

Требуется разработать такой план распределения ТС по объектам, при котором суммарное время простоев ТС будет минимальным.

Последовательность действий выбора наилучшей альтернативы методом потенциалов.

* составляем исходный план распределения машин по следующим правилам:

а) в правом верхнем углу клеток таблицы поместим цифры простоев ТС, а в левые нижние углы тех же клеток цифры характеризующие количество распределяемых единиц ТС.

б) в нижнюю строку исходной отправной таб. Вводится потенциал UВj, а в правый крайний столбец вводится потенциал UАi.

* правило заполнения строк:

а) при заполнение первой строки выбираем направление то, время простоя минимально, т.е А1и Б4, здесь время простоев имеет стоимость С1 4=3. Количество машин на этом направлении устанавливаются как минимальный из их общего количества имеющая на А1 и потребного для Б4=7ед. При таком распределении достигается либо полный расход ТС , данной базы, либо полное насыщение данного объекта. В данной задачи полностью насыщается объект Б4. На базе А1 остается 4ед.

б) остаток ТС на базе А1 целесообразно направить на объект Б3 и по первому плану составляет количество простоев.

в) т.к все ресурсы А1 исчерпаны, а в направлении А1 Б3 остаются потребности в 5ед. Используя правила выше изложенные заполним строки в направлении А2 иА3.

Проверяем теперь соблюдение условий потенциалов для свободны клеток с этой целью просуммируем для каждой из них соотношения потенциалы баз и объектов и сравним их значения с временем простоев проставленных в таб. 12.1.

Проверка соблюдений условий потенциалов для свободных клеток

UБ3=С13-UА1=5-0=5

UБ4=С14-UА1=3-0=3

UА3=С33-UБ3=1-5=-4

UБ2=С23-UА3=3-(-4)=7

UА2=С22-UБ2=4-7=-3

UБ1=С21-UА2=2-(-3)=5

Сравним значения суммы потенциалов баз UАi и UБj с временем простоя таблицы 12.1

UА1+UБ1 5+1 7

UА1+UБ2 7+0 8

UА3+UБ1 -4+5 6

UА2+UБ3 -3+5 5

UА2+UБ4 3-3 9

UА3+UБ4 -4+3=-1 2

Этот план транспортировки распределения средств по объектам и базам является оптимальным , в случаи если хотя бы в одной из клеток нарушены условия по стоимостям простоя, то план подлежит улучшению путеи перехода к следующей итерациональной процедуре.

Резюме:

Из изложенного видно, что оптимизация плана распределения ТС в процессе РУР для транспортной задачи по критерию min простоя сводится в 4 этапа:

1 этап Составление описание задачи и отправной таблицы по строкам.

2 этап Расчет потенциалов

3 этап Расчет псевдо стоимости

4 этап Проверка оптимальности переход к улучшению плана в случаи нарушения условий хотя бы в одной клетке.

методы оптимального распределения однородных и неоднородных ресурсов

Динамическое программирование в задачах распределения однонородных ресурсов.

Впервые, такого класса задач были решены методом динамического программирования применительно к военным целям и метод специально разрабатывался для распределения определенного количества однотипного оружия, по однотипным или разнотипным целям.

Алгоритм метода динамического программирования был перенесен с задач военного характера на задачи которые стоят перед менеджером распределяющего финансирования ресурсов по исполнителям.

Все действия которые менеджер совершает в процессе распределения однородного ресурса, многоэтапный протекающий во времени.

Алгоритм динамического программирования включают следующие этапы:

Общий этап

Имеется некая управляющая операция (распределение финансов генеральным директором) распадающаяся (естественно или исскуственно) на m шагов.

На каждом шаге осуществляется распределение и перераспределение ресурсов участвующих в операции с целью улучшения ее результатов в целом. Эти распределения ресурсов в МДП (метод динамического программирования) называются управлениями U-операциями.

Эффективность операций в целом (приращение денег в банке) оценивается тем же показателем что и показатель эффективности управления. При этом Э(U) зависит от всей эффективности управления на каждом шаге операций. Тогда Э =Э(U)=Э(U1,U2….Un).

Управление при каждом показатель Э достигается max называется оптимальным управлении Uopt

Задачи динамического программирования заключаются в том, в том чтобы определить на каждом шаге Uiopt, где i=(1,m) и тем самым оптимальное управление в целом.

В большинстве задач МДП

Э = Эj max, где Эj-эффективность операций на этом шаге.

Динамическое программирование при решение задач распределения задач распределения ресурсов осуществляется в два круга. В начале от последнего шага к первому. Затем в обратном направлении от первого к последнему.

На первом круге (от последнего шага к первому) находится условно-оптимальное управлении.

Оно выбирается таким чтобы все предыдущие обеспечивали max Эi+1го шага. Иначе на каждом шаге имеется такое управление Ui которое обеспечивает оптимальное продолжение операции при Эi-1 или Эi+1.Этот принцип выбора управления называется принципом оптимальности Белмона. Так продолжается до первого шага.

Поскольку первый шаг имеет предыдущего, то полученные для него условное Uopt терпит свой условный характер и становится просто оптимальным управлением, играющий роль исходного для второго круга.

Второй круг оптимизации начинается с первого шага для каждого оптимального управления U1opt известно, имея все шаги после него устанавливают Uiopt оптимальное управление становится понятным или известен алгоритм действий который при его реализации на 2м круге обеспечит оптимальность всей операции в целом. На практике встречается много задач по распределению однородных ресурсов решаемых МДП, одно наиболее часто к этому методу приходится прибегать в задачах распределения однородных ресурсов.

Обычно в задачах распределения однородных ресурсов имеет место многоэтапность процессов, протекающих во времени.

В методе динамического программирования имеется некоторая управляемая операция (процесс - объект), распадающаяся на m-этапов. На каждом этапе осуществляется распределение n- нераспределенных ресурсов, участвующих в операции с целью улучшения ее результатов в целом.

Эти распределения ресурсов в динамическом программировании называются управлением операцией (процесс преобразования управляющего ресурса в управляющее воздействие).

Эффективность операции в целом оценивается тем же показателем, что и эффективность ее управления.

При этом Э(U) зависит от всей совокупности управлений на каждом этапе операции:

Закон управления, при котором показатель достигает max, называется оптимальным управлением ( ).

Задача динамического программирования всегда требует определить оптимальное управление на каждом этапе , i = (1,m) и тем самым оптимальное управление в целом.

В большинстве задач, в том числе и задач распределения ресурсов требуется обеспечить:

, где - эффективность операции на i- этапе процесса (операции).

Все вышеизложенное является постановкой задач динамического программирования в общем виде.

Примечание:

задача ДП как и другие задачи управления решается при наличии управленческого ресурса.

Решение задач ДП заключается в следующем алгоритме: оптимизация методом последовательных приближений, итераций в задачах ДП производится в 2 круга: в начале от последнего этапа к первому производится распределение начального ресурса от последнего этапа к первому, а затем в обратном направлении от первого к последнему.

На первом круге от последнего этапа к первому находятся т.н. псевдо оптимальное управление (иногда условно оптимальное). Оно выбирается таким, чтобы все предыдущие этапы обеспечивали этапа.

В общем, на каждом этапе имеется такое управление , которое обеспечивает псевдо оптимальное продолжение операции на этапе, этот принцип выбора управления называется принципом оптимальности Беллмана.

Так продолжается до первого этапа, но поскольку перед первым этапом нет предыдущего, то полученное от него псевдо оптимальное управление теряет свой псевдохарактер и становится просто начальным управлением, которое должно быть переведено в оптимальное.

Второй круг оптимизации начинается с первого этапа, для которого псевдо оптимальное управление, полученное на первом круге, переводится в путем вычитания из

(псевдо оптимум), (14.1)

где - разница между начальным значением ресурса на начало года и конечным значением ресурса на конец года.

Имея для всех этапов псевдо оптимальное управление и значения на конец каждого этапа накопленного ресурса (14.1) будем иметь оптимальное управление на каждом этапе второго круга. На этом первая итерация заканчивается. Итерационные процедуры продолжаются до тех пор, пока не будет достигнуто начальное значение начального ресурса, характеризующего возможности субъекта, проводящего операции.

Рассмотрим алгоритм ДП при решении задачи распределения однородного ресурса, имеющей следующие

исходные данные:

Фирма планирует совместную работу сталелитейного и автомобилестроительного заводов на трехлетний период. Начальный запас стали составляет 2300т., начальные мощности 1200т. стали и 200шт. автомобилей в год. Сталь (сырье) расходуется на производство автомобилей в количестве 4т. на 1 автомобиль на автозаводе, а на производство собственной стали на литейном заводе в соотношении 1т. затрат на 4т. выпуска.

Кроме того сталь расходуется на увеличение мощности автозавода в соотношении 10т. затрат, прирост мощности 1 авто в год и на увеличение мощности сталезавода в соотношении 1т. затрат, прирост мощности сталезавода 0,15т. в год.

Решение о распределении стали на следующий год принимается по показателям очередного года.

Требуется определить мах объем выпуска продукции (авто) за весь планируемый период.

Решение сводится к построению процесса распределения начального запаса стали т. по трем потребителям: автозавод на развитие, сталезавод на развитие, сталезавод на собственное производство в течение трех плановых лет. Процесс максимизации выпуска авто складывается из следующих этапов, последовательно протекающих во времени и отражающих реальный процесс.

Этап 1: на сталезаводе

Планирование выпуска объема стали, необходимого для производства авто на автозаводе, исходя из начальной собственной мощности при наличии начального запаса =1200т. , шт.

Этап2: планирование выпуска объема стали на собственное производство определяется коэффициентом пропорциональности равным 1т. затрат на 4т. выпуска = 0,25

Этап3: планирование выпуска объема стали на увеличение мощности сталезавода

= 0,15т. к 1т. затрат.

На автозаводе:планирование выпуска авто, исходя из начальной мощности завода .

Планирование выпуска объема авто с учетом мощности ее развития.

= 4т./10т. затрат =0,4

Согласно методу динамического программирования применительно к нашей задаче имеем 3 управления: в каждом плановом периоде соответственно.

На основании вышеизложенного алгоритма составляем исходную таблицу:

	Развитие автозавода =0,4	Развитие сталезавода =0,15	Собственное развитие сталезавода =0,25
1	200(1+0,4) = 280	1200*1,15 =1380	4*280*1,25 =1400
2	280(1+0,4) =392	1380*1,15 =1587	4*392*1,25 =1960
3	392(1+0,4) =548	1587*1,15 =1825	4*548*1,25 =2740

1220 4792 6100

Определить псевдо оптимальное управление первого круга, начиная с третьего периода.

Здесь наша задача заключается в том, чтобы найти количество стали необходимое для выпуска авто в каждом периоде.

На втором плановом периоде:

На первом плановом периоде:

На втором круге оптимизации при определении оптимального управлений и при переходе к ним от псевдооптимальных имеем =850т.

Нам необходимо для производства 280 авто на начало планового периода 850т. стали, а на конец планового периода в соответствии с количеством стали на сталезаводе, выпущенной для развития, в соответствии формулой (14.1) будем иметь оптимальное значение

Определяем оптимальное управление на конец второго периода:

На конец третьего периода:

-355 / 4 = 89 максимально возможный выпуск авто при таком начальном запасе без пересмотра коэффициентов и без пересмотра итерационной процедуры :280+392+548-89 =1131 авто.

Если такой план выпуска авто при таком начальном ресурсе не устраивает менеджера, у него есть инструмент, который позволит ему сменить с 0,4 до цифры другой итерационной процедуры.

Задача: Распределение однородных ресурсов

Пусть имеются 5 видов ресурсов m=5, предназначенных для 4х объектов (этапа производственного плана) n=4. Из предыдущей практики было известно характеристики объектов и ресурсов: материальный эффект, при распределении на j объект любой единицы ресурсов Аi. Коэффициент Li характеризует возможности каждого из ресурсов применительно к конкретному объекту.

Характеристики заданы в таблице 14.1.

Хар-ка ресурсов	1	2	3	4
Ai	16	14	12	2
Li	0,1	0,1	0,1	0,1

Требуется определить количество единиц ресурса Х использование которых на каждом из объектов обеспечить.

Решение:

В данной задаче нет естественного разделения операций на шаге. Такое разделение введем исскуственно в соответствии с требованиями 1го пункта алгоритма. За шаги последовательное распределение ресурсов по объекту n=4.

На первом шаге обозначим Х1-количество ресурсов направляемых на 4-й объект, счет шагов с конца. При этом расчет эффективности этого решения, в силу специфических особенностей задачи планирования производства, произведенных по выражению.

Э1=f1(x1)=A4Pi=A4(1-e^-L4X1)=2(1-е^-0,1х1) 14.1

Где Рi=1-е^{-Li х1}

В выражении 14.1 значение х1, известно т.к это количество ресурсов, которое осталось от условного оптимального U управлении на предпоследних от конца (2м от конца шаге).Переберем все возможные значения х1 и для каждого из них рассчитываем f1(х1) или Эi.

Как видно из условий задачи х1 может принимать значения m=0,1,2,3,4,5. Подставляем в 14.1 значения m и после расчетов получаем:

Х1	f1(Х1)
0	0
1	0,19
2	0,363
3	0,518
4	0,659
5	0,787

На втором шаге (с конца) выделяется Х2 ресурсов, а соответственно Э2=f2(х2) должно учитывается по мимо эффекта от второго шага также эффект в результате условно – оптимального управления на первом с конца шага, тогда;

Э2=f2(X2)=Аn-1[1-е^-Ln-1(x1-x2)] 14.3

Max – ый эффект получаемый за 2 шага получается по формуле. Подставляя значения A3 и L3 в 14.2 и проведем расчеты для распределения ресурсов на втором шаге.

Таблица 14.3

Х2	f2(Х2)	Х1(Х2)
0	0	0
1	1,15	0
2	2,175	0
3	3,108	0
4	3,954	0
5	4,722	0

В таб. 14.3, по формуле 14.2 проведены расчеты всех возможных расчетов Х2. Эффективности и одновременно определены значения Х2 зависящие от Х1 при котором f2(х2) достигает max.

Далее аналогично определяем для всех возможных Х3 значения f3(Х3) и Х3(Х2). Таб 14.4

Х3	f3(X3)	Х3(Х2)
0	0	0
1	1,33	0
2	2,541	0
3	3,508	2
4	4,68	2
5	5,804	2

Э3=f3(Х3)=А2(1-е^{-L2{x3-f2(x2)}})

Аналогичным путем рассчитываются условно – оптимальное на 4ом шаге с конца на первом с начала, но но на этом шаге имеется исходная начальная единица ресурсов предназначена для всех этапов, то начинается 2й круг оптимизации в обратном порядке.

По сколькую в начале для всех объектов имеются 5ь единиц ресурсов m=5, а после выделения ресурсов на один из объектов в соответствии с условно – оптимальным управление Х3(Х2)=2, то тогда Х4(Х3)=3

Х4=U4=5ед-2ед=3ед.

Оптимальное управлении на 3ем с конца шаге должно быть таким, что при распределении оставшихся 3х единиц ресурса выдерживался принцип оптимальности при этом Х3=2 Х1=3 Остальные 0

В этом случаи Э =16(1-е^-0,1*3)+14(1-е^-0,1*2)=6,68 суммарный эффект.

Резюме:

Изложенный алгоритм динамического программирования применительно к задачам распределения ресурсов по этапам производственного позволяет в соответствии с принципом Басмана получить оптимальное управление по всему плану путем получения условно – оптимальных управлений на каждом из его этапов и шагов.

Нелинейное программирование в задачах распределения разнородных ресурсов.

Нелинейное программирование (НП) – это математические методы определения max или min целевой функции при наличии ограничений в виде неравенств или уравнений.

Целевая функция или хотя бы одно из ограничений – нелинейное.

Смысл решения задач НП заключается в определении условий, обращающих ЦФ в экстремум.

Нелинейное программирование НП – это метод выбора наилучшего плана распределения неоднородных ресурсов, доставляющий в экстремум ЦФ.

Методом НП решаются задачи распределения неоднородных ресурсов при следующей формулировке её в общем виде.

Пусть имеется m разнородных ресурсов, которое предполагается распределить по n потребителям.

Известны либо оценочные, либо вероятностные возможности переработки i-ого ресурса j-ым потребителем, а так же эффективность использования Э_ij

Распределение ресурсов по потребителям характеризуется параметром управления

, где 0 – если i-ый ресурс не направляется j-ому потребителю, а 1 –наоборот

требуется распределит ресурсы по потребителям так (т.е. выбрать такие значения U_ij), что бы величина:

1. суммарной эффективности использования всех видов ресурсов была max.

2. что бы величина полной вероятности достижения целевой функции была max.

Рассмотрим первый случай .

Для него (13.1)

Где x_ij –кол-во ресурсов i-ого типа, назначенные j-ому потребителю при ограничения 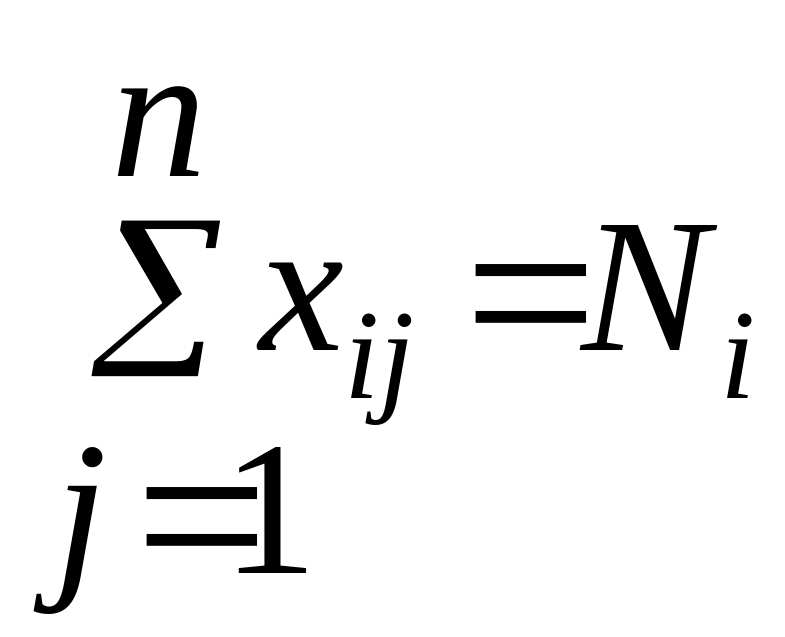(13.2)

Где N_i – кол-во единиц ресурса i-ого вида

Задача

Даны 2 группы разнородных ресурсов (m=2), которые можно включить в 3 проекта (n=3)

В первой группе ресурсов 6 единиц (N₁=6); во второй группе – 10 ед. (N₂=10).

Оценки важности проектов заданы таблицей.

Проекты	1	2	3
Pj – оценка	0,3	0,2	0,5

Эффективность вложений ресурсов различного рода Э_ij задана в таблице

Номер групп ресурсов	Номера проектов
	1	2	3
1	0,4	0,1	0,5
2	0,2	0,4	0,2

Распределение ресурсов по проектам характеризуется исходной матрицей

А = ||X_ij||

Требуется распределить разнородные ресурсы так по проектам, чтобы Э_Σ=max

Решение выполняется итерационным процессом

Алгоритм решения:

1. В области изменения максимизирующей функции определяется исходная отправное допустимое решение Э_ij удовлетворяющая ограничительные условия задачи.

2. с помощью специального Е критерия проверяется достаточно ли близко полученное решение к оптимальному (жилаемому).

3. если полученное отклонение , то путём построения, так называемого, возможного направления и определения в этом направлении конечного шага приближения к оптимуму, получают новое допустимое решение, которое увеличиное значение макс.функции.

4. процесс расчётов носит характер итерации, на котором до полученного решения с максимальным откланением (min^(K)>Δ).

это и будет решение близкое с заданной точностью приближения Е.

реализация расчётов по алгоритму.

1. определяется отправное допустимое решение А⁽⁰⁾=||x_ij⁰||

где, А⁰ – матрица, характеризующая отправное распределение ресурсов по проектам.

Примечание: в качестве отправного распределения может быть взято любое (и произвольное в том числе) распределение с ограничительным условием задачи.

Чем отправное распределение ближе к оптимальному, тем меньше итераций понадобится.

Берём произвольно

Столбцы – номера проектов

Строки – номера видов ресурсов

Далее осуществляется итерационная процедура. В результате выполнения к – итераций, получается К-ое приближение к оптимальному.

2. Определяется компонента матрицы возможного направления итерационных шагов, имеющая вид:

S^(K)=||S_ij^(K)||, где S_ij^(K)=

Величина находится с помощью матрицы y_ij^(K).

Резюме: при заданном Е критерии 0,01 необходимо после шага 4 итерации. В которых Δ^(K) больше Е кроме 4-ой итерации.

Точность приближения к оптимуму определяются ЛПР и Е может ровняться и 0,02; и 0,01; и 0,1; и 0,2. Примечание : в курсовых работах точность должна быть не менее 0,1.

методы оптимизации закупок и запасов продукции

Вероятностные методы принятия решений в задачах оптимизации закупок

Вероятность какого-либо события – это отношение количества исходов (m) в опытах к общему количеству опытов (n).

P = m/n 16.1.

Априорная вероятность (доопытная) – вероятность события до проведения эксперимента.

Апостериорная вероятность (послеопытная) - вероятность наступления события в конце эксперимента.

Безусловная вероятность – вероятность наступления события, не связанного в опыте ни с каким другим событием. ( ).

Условная вероятность – вероятность события T при условии, что произошло событие S. ( ).

Формула полной вероятности:

(16.2), где: - безусловная вероятность события T; - условная вероятность того, что событие Т наступит при наступлении события ; - априорная вероятность события .

Формула Байеса:

(16.3)

Пример. Прогноз погоды на 12 июня показал, что день будет солнечным (событие ). Этот прогноз может быть ошибочным с условными вероятностями P( / )=0.9 и P( / )=0.3; апостериорные вероятности событий: - солнце, - дождь; априорные вероятности: P( )=0,8, P( )=0,2. тогда по формуле Байеса найдем апостериорные вероятности:

P =(0.9*0.8)/(0.9*0.8)+(0.3*0.2)=0.923 – вероятность солнца;

P =1-0.923=0.0769 – вероятность, что пойдет дождь. При решении задач, содержащих случайные события, необходимо иметь статистику наступления этих событий. Этой статистикой менеджер располагает практически всегда. Используя такую статистику, менеджер может с успехом решать задачи, в которых имеется зависимость конечного результата от случайного спроса.

Обычно такой класс задач подразумевает наличие трех видов критериев в принятии решений:

1. max-max (т.е. максимальный из максимумов);

2. min-max (минимальный из максимумов);

3. max-min (максимальный из минимумов).

Используя такого плана критериев, можно оперировать при решении задач оптимизации закупок, оптимизации создания резерва запасов и других аналогичных задач. Можно использовать как вероятностный подход, так и без учета вероятности.

При вероятностном подходе часто используется статистическая средняя математического ожидания, имеющая вид:

(16.4).

Пример. Определить среднюю длину куска ткани, если результаты замеров представлены в таблице:

длина	42	41	40	39	38	37	n
частота							100
m	5	15	60	10	8	2
P=m/n	0.05	0.15	0.6	0.1	0.08	0.02

= (42*0,05)+(41*0,15)+(40*0,6)+(39*0,1)+(38*0,08)+(37*0,02)=40,5м

Задачи по оптимизации закупок

Описание. Владелец кондитерской ежедневно закупает пирожное по С= 7руб. за 1шт., а продает по Ц=13руб. На следующий день оставлять пирожное нельзя, поэтому в конце дня он проводит распродажу оставшихся пирожных поЦр= 3руб. за штуку. Статистика фактических данных о реализации пирожных за прошлые 50 дней приведена в таблице.

Фактический спрос на пирожное

Спрос шт/день	1	2	3	4	5	результат
частота	5	10	15	15	5
P=m/n	0.1	0.2	0.3	0.3	0.1

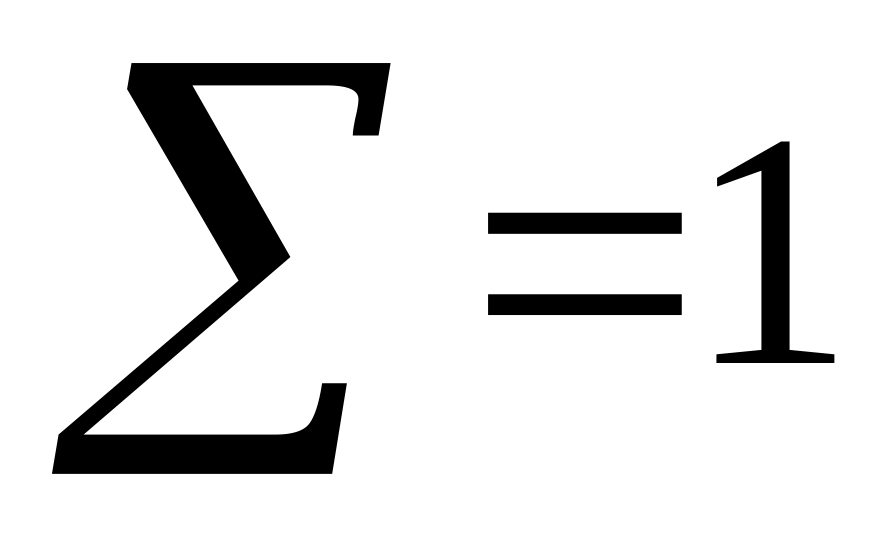
Требуется определить, сколько пирожных необходимо закупить на следующий день, используя вышеуказанные критерии (max-max, min-max, max-min).

Решение. Рассчитаем в следующих таблицах доходы и убытки в день, которые будут зависеть от количества закупаемых и реализованных пирожных.

Строим матрицу по доходам

Закупки N	1	2	3	4	5
Спрос M
1	6	2	-2	-6	-10
2	6	12	8	4	0
3	6	12	18	14	10
4	6	12	18	24	20
5	6	12	18	24	30