15 Вопрос
Размерность линейного пространства:
Линейное пространство V называется n-мерным (имеет размерность n), если в нем:
1) существует n линейно независимых векторов;
2) любая система n + 1 векторов линейно зависима.
Обозначения : n = dim V; .
Базис линейного пространства:
Базисом
в n-мерном
пространстве называется любая
упорядоченная система из n
линейно независимых векторов.
Обозначение:
Теорема о базисе:
Каждый вектор может быть разожжен по базису единственным образом.
16 Вопрос
Действия с векторами в координатной форме:
Пусть
относительно фиксированного базиса
векторного
пространства V над полем K
,
,
где
–
произвольные векторы, и пусть
–
произвольный скаляр. Тогда справедливы
равенства:
1)
или
;
2)
или
.
Другими словами, при сложении векторов их координаты складываются, а при умножении скаляра на вектор его координаты умножаются на этот скаляр.
Преобразование вектора координат при переходе к новому базису:
Теорема.
Пусть
(e)={
}
и (f)={
}—
два базиса в n-мерном линейном пространстве
L.
Координаты
вектора
в
базисе (e)
и координаты
вектора
в
базисе (f)
связаны соотношением
где
,
—
матрица перехода от базиса (e)
к базису (f)
и обратная к ней.
Пример:
)
Дано:
Записать
вектор
в
базисе векторов
.
Решение:
Чтобы
векторы образовывали базис нужно, чтобы
они были некомпланарны, т.е. их векторное
произведение (объем параллелепипеда
на векторах) не равнялось нулю.
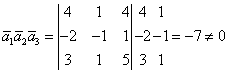Вектор
в старом базисе:
В
новом:
Старые
координаты связаны с новыми
Решив
эту систему с помощью обратной матрицы,
найду координаты вектора
в
новом базисе
Матрица,
связывающая старые и новые координаты:
Новые
и старые координаты связаны
отношением:
b=BbI
b – матрица
старых координат;
B – матрица,
связывающая координаты старые и новые;
BI
– матрица новых координат.
Отсюда:
bI=B-1b
Найду
обратную матрицу B-1.
Определитель
≠0 , значит обратная матрица существует.
Найду
алгебраические дополнения:
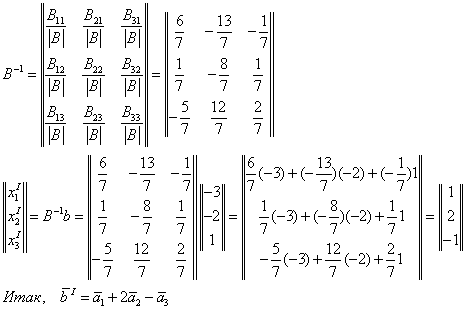
17 Вопрос
Линейное подпространство линейного пространства
Определение.
Множество M векторов линейного пространства
L, такое, что для любых
и
из
M и любого числа
справедливо
,
называется линейным подпространством
линейного пространства L.
Всякое подмножество элементы которого в свою очередь образуют линейное пространство называются подпрастранством.
Линейное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр.
Пример. Множество M арифметических векторов из Rn, у которых последние компоненты — нулевые, образует линейное подпространство в Rn:
Можно
доказать, что если M — линейное
подпространство линейного пространства
L, то нулевой элемент пространства L
принадлежит M и если
,
то и
.
Справедливо следующее утверждение
Линейное подпространство линейного пространства является линейным пространством.
Чтобы подмножество было подпространством, необходимо и достаточно, чтобы
;для всякого вектора
,
вектор
также
принадлежал K,
при любом
;для всяких векторов
,
вектор
также
принадлежал K.
Последние два утверждения эквивалентны следующему:
для всяких векторов , вектор
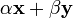также
принадлежал K
для любых
.