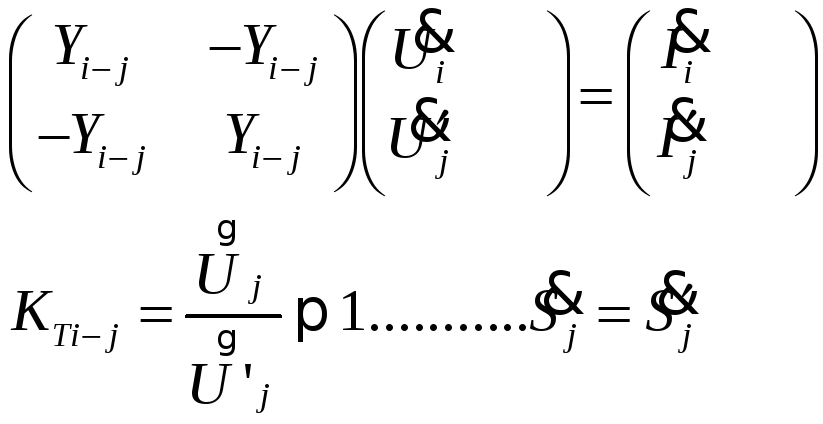Алгоритмы - шпоры (Final)

1’ Области рационального использования средств ВТ. Характеристики каждой из областей.

1’ Эксплуатационные расчёты:

а) прогнозирование графика нагрузки.

б) оценка состояния (формирование модели режима на основе телеизмерений,

расчёт режима)

в) расчёт токов КЗ

г) расчет переходных процессов

д) оптимизационные расчеты

2’ Проектные расчёты:

а) расчёты режимов

б) расчет токов КЗ

в) расчет устойчивости

г) выбор трассы линии, выбор конфигурации сети, определение осуществимости.

3’ Планирование развития ЭС:

Решается сложная оптимизационная задача, но с учетом ограничений:

- по устойчивости

- по надежности

- по качеству

4’ Научные исследования.

- от расчёта устойчивости до синтеза структуры автоматического регулирования

5’ Применение компьютеров в контурах управления (противоаварийная автоматика, …), т. е. выполняется задача информационно-вычислительного обеспечения диспетчера.

Несмотря на высокое развитие, факторы экономного использования памяти не потеряли своей актуальности.

2’ Техническая постановка задачи расчету установившегося режима. Самостоятельное и подчиненное значение расчетов УР. Результаты расчета УР

Получение параметров УР имеет самостоятельное значение, т.е. позволяет ответить на вопрос, осуществим ли режим (возможна ли передача мощности от источника к потребителю, меньше ли допустимых значений токи в элементах сети, допустимы ли значения напряжений в узловых точках сети).

Помимо этого, результаты расчёта УР могут являться данными для других расчётов (подчиненное значение):

- проверка статической устойчивости

- проверка динамической устойчивости

- расчет токов КЗ

- решение задач по эквивалентированию.

В результате расчета УР находим:

- напряжения в узлах ЭС

- потокораспределение в сети

- суммарные потери активной и реактивной мощности

- некоторые специаьлные программные комплексы позволяют также:

а) учесть изменение частоты

б) осуществить проверку апериодической статической устойчивости

в) судить о точности измерений (контрольные замеры)

3’ Классификация элементов ЭЭС (активные, пассивные, узловые, линейные). Модели всех элементов ЭЭС. Классификация узлов.

Для выполнения расчетов УР ЭС необходима информация о схеме сети и её параметрах, о потребителях (нагрузках подстанций) и источниках электроэнергии (электростанциях), т. К. реальными элементами энергосистем являются:

1) генераторы электростанций (СГ), синхронные компенсаторы (СК), статические тиристорные компенсаторы (СТК) и другие источники.

2) нагрузки подстанций, представленные в виде мощности нагрузки Sн, управляемого шунтирующего реактора (УШР) или в виде проводимости шунта нагрузки Yш. 3) электрическая сеть – элементы, передающие и преобразующие электроэнергию, т. е. ЛЭП, трансформаторы и автотрансформаторы, а также нерегулируемые статические устройства продольной и поперечной компенсации, схемы замещения которых содержат активные, индуктивные и емкостные сопротивления, образующие продольные или поперечные (связанные с нейтралью) ветви. Все реальные элементы энергосистемы можно разделить на активные и пассивные. Активные – элементы, генерирующие и потребляющие электроэнергию, которые в расчетах УР представляются в виде источников тока (задающих токов). В ряде случаев ветвь намагничивания Т или АТ вводится постоянным отбором мощности, задаваемым аналогично нагрузке, в виде источника тока. Пассивные – элементы, параметры схем замещения которых в расчетах УР принимаются постоянными, не зависящими от напряжений и токов в этих элементах

Все активные элементы – узловые, т.е. поперечные ветви.

Пассивные эл-ты – узловые (поперечные) или продольные ветви.

Для расчёта УР все реальные эл-ты должны быть смоделированы. Расчетная схема эл. системы составляется на 1 фазу с нейтралью.

4’ Модель ветви, модель узла. Генераторные, нагрузочные узлы. Базисный уз.

Для расчёта УР все реальные эл-ты должны быть смоделированы. Расчетная схема эл. системы составляется на 1 фазу с нейтралью. Обычно все элементы, классификация которых приведена выше, ипользуются в современных ПВК для расчета режимов и укладываются в 2 модели элементов ЭС.

1) Модель ветви. Т.к. в состав продольных элементов входят не только линии электропередач, но и трансформаторы или АТ, то модель ветви представляется как модель ЛЭП (П-образная сх. замещ-я) + модель Т или АТ (Г-образная сх. замещ-я). Если схема замещения электрической системы не приводится к одной ступени напряжения, то в схемы зам-я тр-рных эл-тов вводятся идеальные к-ты трансф-ции.

2) Модель узла. Каждый узел может характеризоваться в расчете УР следующей парой параметров:

- активной и реактивной генерируемой мощностью Pг, Qг

- комплексным напряжением (модулем Ui, фазой δ)

- активной и реактивной мощностью нагрузки Pн, Qн

- активной и реактивной проводимостью на землю (Yш=g+-jb)

5’ Обобщённая статическая характеристика по напряжению (СХН). Возможность представления нагрузки различными способами на основе СХН.

а) представление нагрузки постоянным сопротивлением:

б) представление нагрузки постоянным током:

в) представление нагрузки постоянной мощностью:

6’ Представление исходных данных об ЭЭС для расчета УР в ней.

Таблица по формату f8.0, включает в себя массивы узлов и ветвей.

Массив узлов:

- код массива (0201)

- номер узла

- Uном – номинальное напряжение в узле

- Pг – активная генерируемая мощность

- Qг – реактивная генерируемая мощность

- Pн – активная мощность нагрузки

- Qн – реактивная мощность нагрузки

- Umod – модуль напряжения в узле

- Qmin – ограничение по генерируемой мощности

- Qmax - ограничение по генерируемой мощности

Массив ветвей:

- код массива (0301)

- Nn - номер узла начала ветви

- Nk - номер узла конца ветви

- R – активное сопротивление ветви

- x – реактивное сопротивление ветви

- Yc – проводимость ветви на землю

- Tk – коэффициент трансформации

- Tf – коэффициент трансформации

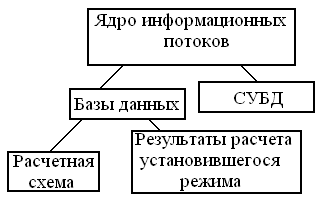
7’ Ядро информационно-вычислительной системы. База данных. Модели данных. СУБД и ее функции.

Основные модели баз данных:

1. Иерархическая (дерево)

2. Сетевая (самопроизвольная связь)

3. Реляционная (таблица). Достоинство: простота модификации и логичная структура. Недостаток: Медленнодействующая.

СУБД – совокупность языковых и программных средств, обеспечивающих доступ, управление, создание баз данных.

Функции СУБД:

1. Формирование БД (начальное заполнение)

2. Модификация структуры БД и изменение записей.

3. Сортировка и упорядочение данных.

4. Генерация отчетов

5. Обработка стандартных запросов

6. Интерфейс с другими программными продуктами

8’ Основные уравнения, описывающие установившийся режим ЭЭС. Узловое уравнение состояния ЭЭС (в форме баланса токов, мощности).

Из (1) и (2) =>

- Узловое уравнение в форме баланса токов.

- Узловое уравнение в форме баланса мощности.

Y – матрица узловых проводимостей, размерность (n*n)

U – вектор-столбец междуфазных, линейных значений

напряжений. (столбец неизвестных (nx1) )

S - столбец заданных мощностей  

Uд^-1 - квадратная матрица (nxn), в которой присутствуют элементы только на главной диагонали.

Система (2) – нелинейна.

Допущения:

1. Вся система приведена к одному номинальному напряжению

2. Все мощности в узлах заданы (все генераторные узлы – неопорные)

Примечение: ^ - сопряженное значение

· - комплексное значение

9’/11’ Базисный и балансирующий узлы. Требования к выбору балансирующего узла.

Балансирующий узел => не задана мощность => после решения

системы (n-1) уравнений можно будет найти Sбал куда будут включены все небалансы.

Базисный узел – столбец.

Балансирующий узел – строка.

Требования к выбору балансирующего узла:

1. Мощность станций, связанных с балансирующим узлом должна быть на порядок больше мощностей остальных станций в исследуемой ЭС.

2. В балансирующем узле должны быть резервы активной и реактивной мощности.

3. Напряжение в этом узле не должно зависеть от режима.

4. Этот узел должен быть наиболее мощной станцией в ЭС, либо это д.б. часть другой ЭС, высшей ступени иерархии (сэквивалентированная).

Про базисный:Если - решение системы уравнений,то

- так же решение этой системы.

Доказательство:

Следовательно, чтобы избежать неоднозначности системы решений, необходимо задать базисный узел, где δбаз=0.

10’ Базисный узел. Необходимость задания базисного узла в расчетах УР.

1. Если - решение системы уравнений, то и

- так же решение этой системы.

Доказательство:

Следовательно, чтобы избежать неоднозначности системы решений, необходимо задать базисный узел, где δбаз=0.

2.

Если мы задали мощности => мы задали потери, а потери, в свою очередь, зависят от напряжения, которое является неизвестным.

=> Во всех узлах задать мощность нельзя.

В базисном узле необходимо задать модуль напряжения и его фазу.

=> Вычеркиваем столбец базисного узла => (n-1) неизвестное напряжение

=>Необходимо вычеркнуть уравнение балансирующего узла, в котором задана мощность.

12’ Узловое уравнение состояния ЭЭС в форме баланса токов или мощности при условии совмещения базисного и балансирующего узлов.

Узловое уравнение в форме баланса токов.

Узловое уравнение в форме баланса мощности.

Y – квадратная матрица узловых проводимостей, размерность

(n-1)*(n-1)

U – вектор-столбец междуфазных, линейных значений

напряжений. (столбец неизвестных (n-1)x1

^

S - столбец комплексно-сопряженных значений мощности в узлах схемы зам. (n-1)*1

^ ^

Uд^-1= diag(1/Ui) - диагональная матрица комплексно сопряженных значений в узлах схемы зам. (nxn), в которой присутствуют элементы только на главной диагонали.

Yjбаз – столбец проводимостей ветвей, связанных с базисным узлом. (n-1)*1

Uбаз – напряжение в базисном узле.

13-14’ Формирование матрицы узловых проводимостей. Алгоритм и программная реализация

1)Если среди элементов, ограничивающих ветвь i-j нет «земли», то она формирует 4 эл-та матрицы Y.

2)Если среди номеров узлов, ограничивающих ветвь, есть ветвь земли, то проводимость этой ветви входит только в 1 диаг. элемент

Y_ii = Y₂₂ → +Y_2-0

Программная реализация (↓ - переход на новую строку)

Subroutine matry (nn,nk,z,yc,m,n,y,l)

Dimension nn(1),nk(m),yc(n)

Complex z(m), y(l,l)

Do i=1,n ↓ do j=1,n ↓ y(i,j)=(0,0) ↓ end do ↓ end do ↓ do i=1,n ↓ y(i,j)=(0,0) ↓ do k=1,m ↓ i=nn(k) ↓ j=nk(k) ↓ c=(1,0)/z(k) ↓ if(i*j.ne.0)then ↓ y(i,j)=-c ↓ y(j,i)=-c ↓ y(i,i)=y(i,i)+c+0.5*cmplx(0,yc(k)) ↓ else ↓ j=i+j ↓ end if ↓ y(j,j)=y(j,j)+c+0.5*cmplx(0,yc(k)) ↓ end do ↓ end do

15-16’ Учет трансформаторных связей при формировании матрицы узловых проводимостей

17’ Прямые и итерационные методы решения систем линейных алгебраических уравнений (СЛАУ). Необходимость использования этих методов для решения задач расчета установившихся режимов.

1) прямые (точные) методы – дают решение за конечное число арифметических итераций, которое определяется вычислительной схемой метода а также порядком и структурой матрицы коэффициентов СЛАУ. (Гаусса)

2) Итерационные – это методы, в которых за счет многократного выполнения однообразных вычислений (итераций) получается решение с наперед заданной точностью. Чем выше точность, тем больше количество итераций. (м. Зейделя, min ф-ции ошибки, релаксационные методы)

2ое уравнение (бал. мощностей) – сугубо нелинейное – решается с помощью линеаризации в каждой точке.

Матричные узловые ур-я в форме баланса токов или мощностей – это системы нелинейных уравнений, которые характеризуются как простотой формирования, так и большими возможностями с точки зрения эффективной организации процесса их решения. Нелинейные Ур-я содержат в общем случае n комплексных уравнений с n комплексными неизвестными напряжениями в узлах

В результате получаем СЛАУ, которую необходимо решать на каждой итерации.

18’ Метод Гаусса с обратным ходом. Вычислительная схема пр и обр хода. +/- метода

1 этап: Прямой ход: n шагов – матрица коэффициентов приводится к треугольному виду:

2 этап: Обратный ход – находятся X_n-1,….X₁

1 этап: , а для для К-го шага:

2 этап:

«+» : 1) прямой (точный) метод, получаем решение за конечное число шагов. 2) если диагональн элементы >> недиагональных, то хорошая точность расчета

«-» : 1)вычисления по формулам (2) и (3) дают большую погрешность, если диагональн элементы → 0 (малы)

2)вычисления по формулам (4) и (5) могут дать большие погрешности, если вычитаются близкие величины (при detA → 0). Неточность задания исходных данных может привести к большой погрешности, ПРИМЕР: сис-ма уравнений 1000x₁+x₂=1002; 2001x₁+2x₂=2005; решая ее получим x₁= 1, x₂= 2. Изменив исх данные с ε=0,1% система будет: 1001x₁+x₂=1002; 2001x₁+2x₂=2005; решив новую систему получим: x₁= -1, x₂= 2003.

3)При выполнении прямого хода метода Гаусса первоначально слабозаполненная матрица коэффициентов, если не принять спец. мер, после 1го шага оказывается полностью заполненной.

19’ Алгоритмическая и программная реализация метода Гаусса с обратным ходом.

Алгоритм:

Прямой ход:

Обратный ход:

20’ Принципы учета слабой заполненности сетевых матриц при использовании метода Гаусса.

1) Порядок исключения ненулевых элементов в методе Гаусса должен быть таким, чтобы в процессе исключения появились минимальное кол-во новых ненулевых элементов;

Итог: 1) Надо либо менять порядок следования исходных узлов

2) Либо не изменяя порядка исключения переименовывая узлы (см билет 23)

Порядок исключения: в первую очередь должны исключаться узлы менее всего связанные с другими узлами (имеющие наименьшее число инцидентных связей с другими элементами)

2) Хранить в памяти машины нужно только ненулевые элементы и только с ними нужно производить арифметические операции (см билет 24)

21’ Порядок исключения неизвестных в методе Гаусса с обратным ходом.

1) Порядок исключения ненулевых элементов в методе Гаусса должен быть таким, чтобы в процессе исключения появились минимальное кол-во новых ненулевых элементов;

Итог: 1) Надо либо менять порядок следования исходных узлов

2) Либо не изменяя порядка исключения переименовывая узлы (см билет 23)

Порядок исключения: в первую очередь должны исключаться узлы менее всего связанные с другими узлами (имеющие наименьшее число инцидентных связей с другими элементами)

2) Хранить в памяти машины нужно только ненулевые элементы и только с ними нужно производить арифметические операции (см билет 24)

22’ Коэффициент заполненности матриц. Хранение ненулевых элементов матриц.

- кол-во элементов; n – кол-во узлов; m – ветвей

В больших схемах

Вывод: чем больше кол-во узлов схемы тем меньше коэффициент заполненности

Хранить необходимо только ненулевые элементы матрицы Y, причем только верхний Δ, так как матрица Y – симметрична

(см билет 24)

Требования к схемам хранения матриц.

1) Компактность

2) Простота формирования

3) Простота использования

а) простота выборки элементов

б) гибкость изменения хранимой информации

(т.к. поле 1 шага появл. новые ненул элементы)

I. Задаем только ненул. элементы:

Экономия от n² до 4n чисел

23’ Алгоритмы упорядочения, их классификация.

2) компромисс между программно не очень сложной перенумерацией и экономией памяти машины

3) процесс упорядочивания проходит до начала исключения узлов

4) осуществляется на каждом шаге прямого хода

5) нумерация, предполагающая миним. требуемый объем памяти, мин. суммарное кол-во ненулевых элементов

При программной перенумерации происходит только имитация процесса исключения неизвестных

24’ Хранение слабозаполненных матриц. Схемы упаковки матриц. Требования к схемам хранения матриц.

1) Компактность

2) Простота формирования

3) Простота использования

а) простота выборки элементов

б) гибкость изменения хранимой информации

(т.к. поле 1 шага появл. новые ненул элементы)

I. Задаем только ненул. элементы:

Экономия от n² до 4n чисел

II. Организуем отдельно массив диагональных элементов, для которых не храним номер строки и столбца:

III.

IV.

25’ Алгоритм формирования матрицы У в компактной форме.

Только те эл-ты, которые есть в верхнем Δ

Создается доп массив NADR – номер ячейки массива VALUE, с которого начинаются проводимости, связанные с этим узлом

7 – потому что 6 эл-тов всего в VALUE, показывает что больше ни с чем не связано.

26’ Алгоритмическая и программная реализация формирования матрицы Y в компактной форме.См.25 Программа:

Subroutine ysz (nn, nk, z, yc, y, diag, nzero, value, icol, nadr, n, m)

Complex z(m), yc(m), diag(n), value (1)

Dimension nzero(n), icol(1), nadr(n)

do i=1,m

diag(i)=(0.0)

nzero(i)=0

end do; do i=1,m

i1=nn(i)

i2=nk(i)

y(i)=(1,0.)/z(i)

if(i1*i2.ne.0) then j=i2

if (i2.gt.i1) j=i1

nzero(j)= nzero(j)+1

diag(i1)= diag(i1)+y(i)+0.5*yc(i)

else i2=i1+i2

endif

diag(i2)= diag(i2)+y(i)+0.5*yc(i)

end do

nadr(1)=1 do i=2,n

nadr(i)= nadr(i-1)+ nzero(i-1)

end do do i=1,m

i1=nn(i)

i2=nk(i)

if(i1*i2.ne.0) then j=i2

if (i2.gt.i1) j=i1

k=nadr(j)

nadr(j)= nadr(j)+1

value (k)=-y(i)

icol(k)= i1+i2=j

endif

end do end return

27’ Итерационные методы расчета УР. Алгоритм расчета УР методом Зейделя.

1)Поузловые методы – м., где исх переменные ищутся из каждого след. ур-я последовательно.

2)Одноврем. реш. ур. – все ур. системы реш-ся одновременно на каждой итерации.

Бал.токов: метод Гаусса, обращения, факторизации матрицы

Бал. Мощностей: метод Ньютона

Эффективность:

1)кол-во вычислений на кажд. Итерации;

2)суммарное кол-во итераций;

3)суммарное время вычислений.

Нет абсолютно эффективных и абсолютно сходящихся методов

28’ Метод Зейделя применительно к решению нелинейного узлового ур-я в форме баланса токов.

YU=U_д^-1S-Y_jбазU_баз примечание: над U_д^-1S надо ^

Правая линейная часть, левая нелинейная часть.

U₁^(k)=1/Y₁₁*( S₁/U₁^(k-1)- Y_1базU_баз-Y₁₂U₁ ^(k-1)- Y₁₃U₃ ^(k-1)-_….. -Y_1nU_n ^(k-1))

U₂^(k)=1/Y₂₂*( S₂/U₂^(k-1)- Y_2базU_баз-Y₂₁U₂ ^(k)- Y₂₃U₃ ^(k-1)-_….. –Y_2nU_n ^(k-1))

………..

U_n^(k)=1/Y_nn*( S_n/U_n^(k-1)- Y_nбазU_баз-Y_n1U₁ ^(k)- Y_n2U₂ ^(k)-_….. –Y_n-1nU_n-1 ^(k))

Итерационная формула Зейделя:

U_i^(k)=1/Y_ii*( S_i/U_i^(k-1)- Y_iбазU_баз-Σ^(i-1) Y_ijU_j ^(k)-Σ Y_ijU_j ^(k-1))

S_бал=U_балΣY_балjU_j

Должно быть задано макс. кол-во итерацмй,номер балансирующего узла,точность

max ׀U_i ^(k)- U_i ^(k-1)׀≤ε_k≈0.5÷0.05

max ׀P_нб׀≤ε_р ≈ 0.5 МВт max ׀Q_нб׀≤ε_Q ≈ 1 Мвар

Примечание: везде над S/U надо поставить ^