1 Вопрос

Векторным произведением векторов и называется вектор , который определяется следующими условиями:

1. Его модуль равен где - угол между векторами и .

2. Вектор перпендикулярен к плоскости, определяемой перемножаемыми векторами и .

3. -правая тройка (Вектор направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы и , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки)

Свойства:

Геометрические свойства:

1. Модуль этого произведения равен площади параллелограмма на этих векторах как на сторонах, модуль от ( ) = S

2. Векторное произведение 2-х векторов равно 0 тогда и только тогда, когда они коллиниарны (параллельны).

Алгебраические свойства:

1. a*b=-b*a –антипереместительное

2. [k*a , b]=k[a , b] – ассоциативность

3. [a+b , c]=[a , c]+[b , c] – дистрибутивность

Координатная форма:

Пусть ,

Тогда



2 Вопрос

Смешанным произведением трёх векторов называют число, равное

Тоесть здесь первые два вектора умножаются векторно и затем полученный вектор умножается скалярно на третий вектор . Очевидно, такое произведение есть некоторое число.

Геометрический смысл:

Смешанное произведение 3-х векторов равно обьёму параллелепипеда, построенного на этих 3-х векторах как на рёбрах, со знаком + если эти 3 вектора правая тройка. .

Следствия:

1. оббьем параллелепипеда равен

2. (a,b)*c= a*(b,c)

Координатная форма

Если векторы заданы в координатной форме то можно показать, что их смешанное произведение находится по формуле:

Компланарность векторов:

есть необходимое и достаточное условие компланарности векторов , , .

1. Доказательство.

   1. Предположим, что , т.е. , тогда или или .

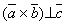Если , то или или . Поэтому – компланарны.

Если , то , , - компланарны.

2. Пусть векторы – компланарны и α – плоскость, которой они параллельны , т. е. и . Тогда , а значит , поэтому или .

3 Вопрос

F(x,y,z)=0 – называется уравнением поверхности П, если ему удовлетворяют координаты точки лежащей на этой поверхности и не удовлетворяют координатам никакой точки не лежащей на ней.

Поверхность П называется поверхностью n-ого порядка, если она определяется алгебраической поверхностью n-ой степени.(где n- наивысшая степень в уравнении).

Любая плоскость задаётся уравнением 1-ой степени:

Ax + By + Cz + D = 0

Уравнение плоскости проходящей через данную точку с данным нормальным вектором:

Теорема. Если в пространстве задана точка М₀(х₀, у₀, z₀), то уравнение плоскости, проходящей через точку М₀ перпендикулярно вектору нормали (A, B, C) имеет вид: 

A(x – x₀) + B(y – y₀) + C(z – z₀) = 0.

Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор . Т.к. вектор  - вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору . Тогда скалярное произведение

 = 0

Таким образом, получаем уравнение плоскости

Теорема доказана.