Кривизна. Радиус кривизны.

Рис. 13.

Пусть M и M₁ – две близь лежащие точки одной линии. и ₁ – орты, проведенные в этих точках к линии. Перенесем орт ₁ в точку M (рис. 13). Угол  между ортами и ₁ называется углом смежности линии на участке MM₁. Средней кривизной линии на этом участке называется отношение угла смежности к длине дуги этого участка:

.

Кривизной линии в точке M называется предел, к которому стремиться средняя кривизна на участке MM₁, когда точка M₁ стремиться к точке M:

.

Радиус кривизны линии  в точке M равен обратной величине кривизны линии в этой точке:

Докажем, что производная орта касательной по длине дуги линии равна отношению орта главной нормали к радиусу кривизны этой линии:

.

Направление вектора  стремиться к направлению орта . Так как, когда точка M₁ стремиться к точке M, вектор  , оставаясь в соприкасающейся плоскости, стремится стать перпендикулярным вектору .

Величина вектора  , как основания равнобедренного треугольника, равна  =2 sin(/2), но =1 – орт, следовательно, при s0  .

Касательное и нормальное и полное ускорения движущейся точки.

Определим ускорение точки, когда её движение задано естественным способом. Подставив выражение (6) в формулу (2), получим:

.

Касательное ускорение точки характеризует изменение вектора её скорости по величине. Вектор касательного ускорения направлен по касательной к траектории движущейся точки в ту же сторону, что и вектор скорости точки, когда движение точки ускоренное, и в обратную сторону, когда – замедленное. Величина касательного ускорения равна первой производной по времени от величины скорости точки:

. (7)

Если касательное ускорение точки равно нулю, то точка движется равномерно.

Нормальное ускорение точки характеризует изменение вектора её скорости по направлению. Вектор нормального ускорения направлен по главной нормали к траектории движущейся точки в сторону вогнутости траектории. Величина нормального ускорения равна отношению квадрата скорости точки к радиусу кривизны её траектории:

. (8)

Если нормальное ускорение точки равно нулю, то точка движется прямолинейно.

Рис. 14.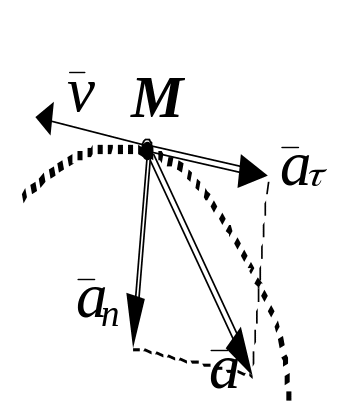

Зная касательное и нормальное ускорение точки, её полное ускорение можно построить (рис. 14), как диагональ прямоугольника со сторонами, равными _ и _n.

Величина полного ускорения точки определяется по теореме Пифагора:

.

Полное ускорение точки характеризует изменение вектора скорости этой точки во времени (и по величине и по направлению).

На рис. 14 полное ускорение точки построено для случая её замедленного движения, так как направление векторов скорости и касательного ускорения противоположно.

Классификация движения точки.

1. Если _= 0, _n= 0, то точка движется равномерно прямолинейно, и её полное ускорение равно нулю: =0.

2. Если _= 0, _n 0, то точка движется равномерно криволинейно, и её полное ускорение равно нормальному ускорению: = _n(8).

3. Если _ 0, _n= 0, то точка движется неравномерно прямолинейно, и её полное ускорение равно касательному ускорению: = _(7).

4. Если _ 0, _n 0, то точка движется неравномерно криволинейно, и модуль её полного ускорения определяется выражением: .