
- •Предмет теоретической механики.
- •Элементы высшей математики.
- •Кинематика.
- •Кинематика точки.
- •Векторный способ задания движения точки.
- •Вектор скорости движущейся точки.
- •Вектор ускорения движущейся точки.
- •Координатный способ задания движения точки.
- •Связь между векторным и координатным способами задания движения.
- •Проекции вектора скорости движущейся точки.
- •Проекции вектора ускорения движущейся точки.
- •Естественный способ задания движения точки.
- •Алгебраическая величина скорости движущейся точки.
- •Связь между естественным и координатным способами задания.
- •Естественная система координат.
- •Кривизна. Радиус кривизны.
- •Касательное и нормальное и полное ускорения движущейся точки.
- •Классификация движения точки.
- •Равнопеременное движение точки.
- •Кинематика твердого тела.
- •Виды движения тела.
- •Поступательное движение тела.
- •Кинематика поступательного движения тела.
- •Вращательное движение тела. Кинематические характеристики тела при вращательном движении.
- •Равнопеременное вращательное движение тела.
- •Скорость точек вращающегося тела.
- •Ускорение точек вращающегося тела.
- •Вращательная скорость. Формула Эйлера.
- •Вращательное и осестремительное ускорение. Формула Ривальса.
- •Кинематика вращательного движения тела.
- •Плоское движение тела. Плоское движение тела– совокупность поступательного и вращательного движения.
- •Кинематические характеристики тела при плоском движении.
- •Скорость точек плоской фигуры.
- •Мгновенный центр скоростей плоской фигуры.
- •1. Доказательство существования мцс.
- •2. Определение скоростей точек плоской фигуры с помощью мцс.
- •3. Способы определения положения мцс.
- •Ускорение точек плоской фигуры.
- •Мгновенный центр ускорений плоской фигуры.
- •1. Доказательство существования мцу.
- •2. Определение ускорений точек плоской фигуры с помощью мцу.
- •3. Способы определения положения мцу.
- •Кинематика плоского движения тела.
- •Касательное и нормальное ускорение точек плоской фигуры.
- •Сферическое движение тела. Углы Эйлера. Уравнения сферического движения тела.
- •Кинематические характеристики тела при сферическом движении.
- •Скорость точек тела при сферическом движении.
- •Ускорение точек тела при сферическом движении.
- •Свободное движение тела. Уравнения и кинематические характеристики свободного движения тела.
- •Скорость точек тела при свободном движении.
- •Ускорение точек тела при свободном движении.
- •Сложное движение точки. Основные понятия сложного движения точки.
- •Скорость точки при сложном движении.
- •Ускорение точки при сложном движении. Теорема Кориолиса.
- •Ускорение Кориолиса.
- •Сложное движение тела.
- •Сложение вращений вокруг пересекающихся осей.
- •Сложение вращений вокруг параллельных осей.
- •Пара вращений.
- •Сложение поступательных движений твердого тела.
- •Сложение поступательного и вращательного движений твердого тела.
- •1. Плоско параллельное движение.
- •2. Винтовое движение.
- •3. Свободное движение.
- •Рекомендуемая литература
- •Оглавление
Свободное движение тела. Уравнения и кинематические характеристики свободного движения тела.
Рис. 43.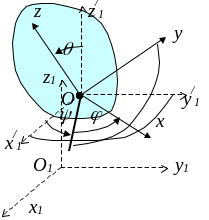
положение другой системы координат Ox/1y/1z/1, движущейся поступательно относительно системы координат O1x1y1z1 вместе с какой-либо точкой O тела,
углы Эйлера, определяющие положение системы координат Oxyz, скрепленной с движущимся телом, относительно системы координат Ox/1y/1z/1.
Зная координаты точки O и углы Эйлера, определяющие положение системы координат Oxyz, можно определить положение любой точки свободно движущегося тела.
Уравнения, определяющие изменение координат точки O и углов Эйлера, описывают движение свободного тела:
xO = x(t), yO = y(t), zO = z(t), , = (t), = (t). (31)
Этих уравнений шесть. Первые три описывают движение тела вместе с точкой O и зависят от выбора этой точки. Вторые три уравнения описывают сферическое движение тела вокруг точки O и не зависят от её выбора.
Поступательное движение свободно движущегося тела вместе с точкой O характеризуется векторами скорости O и ускорения O точки O.
Сферическое движение свободно движущегося тела вокруг точки O характеризуется векторами угловой скорости и углового ускорения .
Скорость точек тела при свободном движении.
Рис. 44.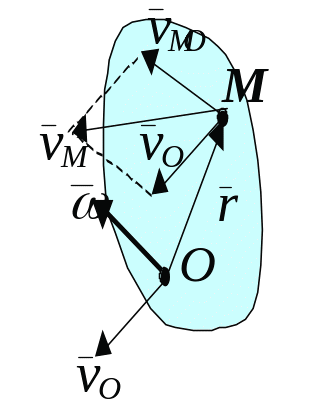
![]() . (32)
. (32)
Ускорение точек тела при свободном движении.
Рис. 45.
![]() .
.
Ускорение MO определяется формулой Ривальса и равно векторной сумме двух составляющих: вращательного ускорения и осестремительного ускорения:
![]() . (33)
. (33)
Вращательное ускорение точки M равно векторному произведению вектора углового ускорения тела на радиус-вектор , соединяющий точку тела O с точкой M (20):
![]() . (34)
. (34)
Осестремительное ускорение точки M равно векторному произведению вектора угловой скорости тела на вектор вращательной скорости точки M (21):
![]() . (35)
. (35)
Сложное движение точки. Основные понятия сложного движения точки.
Если точка M участвует в двух или более движениях, то такое её движение называется сложным движением.
Примером сложного движения точки M является её движение по телу D, движущемуся относительно неподвижной прямоугольной декартовой системы координат Ox1y1z1 (рис. 46). Другую систему координат Oxyz скрепим с телом D. Точка M движется по телу D относительно подвижной системы координат Oxyz.
Рис. 46.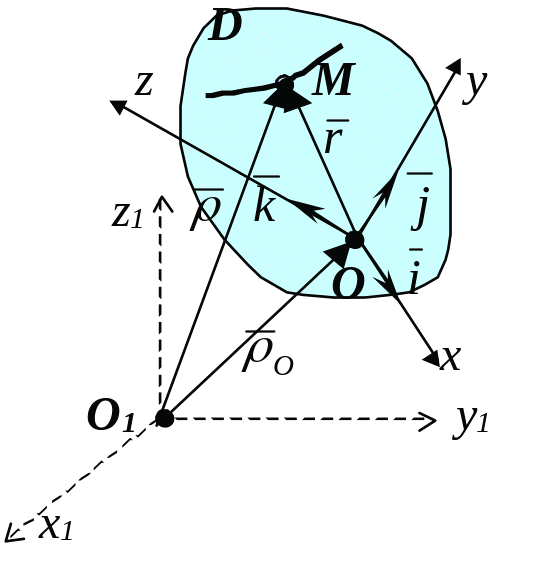
![]() ,
начало которого совпадает с точкой O1,
а конец – с точкой M
(рис. 46). Скорость точки M
относительно неподвижной системы
координат называется абсолютной
скоростью и обозначается
,
начало которого совпадает с точкой O1,
а конец – с точкой M
(рис. 46). Скорость точки M
относительно неподвижной системы
координат называется абсолютной
скоростью и обозначается
![]() .
Абсолютное ускорение
.
Абсолютное ускорение
![]() характеризует изменение абсолютной
скорости точки M
в её абсолютном движении.
характеризует изменение абсолютной
скорости точки M
в её абсолютном движении.
Движение точки M
относительно подвижной системы координат
Oxyz,
связанной с движущимся телом D,
называется относительным
и определяется радиус-вектором
,
начало которого совпадает с точкой O,
а конец – с точкой M
(рис. 46). Скорость точки M
относительно подвижной системы координат
(тела D)
называется относительной
скоростью
и обозначается
![]() .
Относительное
ускорение
.
Относительное
ускорение
![]() характеризует изменение относительной
скорости точки M
в её относительном движении.
характеризует изменение относительной
скорости точки M
в её относительном движении.
Пусть положение осей подвижной системы координат Oxyz определяют орты , и (рис. 46). Зная координаты x, y, z точки M в этой системе координат, можно введенные характеристики определить выражениями:
,
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
Движение точки M
вместе с подвижной системой координат,
связанной с движущимся телом D,
называется переносным.
Скорость той точки тела D,
с которой в данный момент совпадает
движущаяся по телу точка M,
называется переносной
скоростью
точки M
и обозначается
![]() .
Ускорение той точки тела D,
с которой в данный момент совпадает
движущаяся по телу точка M,
называется переносным
ускорением
точки M
и обозначается
.
Ускорение той точки тела D,
с которой в данный момент совпадает
движущаяся по телу точка M,
называется переносным
ускорением
точки M
и обозначается
![]() .
.
