
- •2. Определители матриц. Свойства определителей. Миноры и алгебраические
- •3.Т.Лапласа.Свойства.
- •4 Обратные матрицы и способы их вычисления.
- •5.Решение матричных уравнений.
- •6.Система линейных алгебраических уравнений .Метод Крамера уравнений
- •7 Метод Гаусса.
- •8. Решение произвольных систем. Теорема Кронекера-Капелли.
- •9. Элементарные преобразования матриц. Ранг матрицы. Вычисление ранга матрицы.
- •10.Балансовая модель Леонтьева.
- •11. Собственные числа и собственные векторы .
- •13.Линейная независимость вектора. Базис. Прямоугольная система координат.
- •14.Скалярное произведение векторов и его свойства.
- •15. Векторное произведение векторов и его свойства.
- •16.Смешанное произведение векторов и его свойства.
- •17. Пря Уравнение с угловым коэффициентом.
- •19.Уравнение прямой в пространстве.
- •20. Взаимное расположение прямых и плоскостей.
- •22. Эллипс. Определение. Вывод канонического уравнения.
- •26. Полярные системы координат.
Матрицы. Действия над матрицами и их свойства.
1. Матрицы. Линейные операции над ними и их свойства.
Матрицей называется прямоугольная таблица чисел, содержащая m строк
одинаковой длины.

Матрицы равны между собой, если равны все их соответствующие элементы.
Матрица, у которой число строк и столбцов равно – называется квадратной.
Матрица, все элементы которой, кроме элементов главной диагонали равны нулю,
называется диагональной.
Диагональная матрица, у которой все элементы главной диагонали равны 1,
называется единичной. Обозначается буквой Е.
Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю,
называется треугольной.
Матрица, у которой все элементы равны нулю, называется нулевой.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
2. Умножение матриц. Транспонирование. Свойства.
Операция умножения возможна, если количество столбцов первой матрицы равно
количеству строк другой матрицы.
![]()
где
![]()
![]()
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Матрица, полученная заменой каждой ее строки столбцом с тем же номером,
называется матрицей транспонированной, к данной.
1.
![]()
2.
![]()
2. Определители матриц. Свойства определителей. Миноры и алгебраические
дополнения.
Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно).
1.
![]()
![]()
![]()
2.
![]()
![]()
![]()
3.
![]()
 или
или
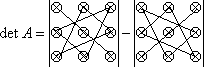
Для нахождения определителя более высокого порядка, матрицу приводят к
треугольному виду и считают произведение элементов на главной диагонали.
Свойства:
1. Определитель не изменится, если его строки заменить столбцами, и
наоборот.
2. При перестановке двух параллельных рядов определитель меняет знак.
3. Определитель, имеющий два одинаковых или пропорциональных ряда,
равен нулю.
4. Общий множитель элементов можно вынести за знак определителя.
5. Если элементы какого-либо ряда представляют собой сумму элементов,
то определитель может быть разложен на сумму двух соответствующих
определителей.
6. Определитель не изменится, если прибавим ко всем элементам ряда
матрицы соответствующих элементов параллельного ряда, умноженных на одно и
тоже число.
7. Определитель равен сумме элементов, умноженных на соответствующее
им алгебраическое дополнение.
8. Сумма произведения элементов одного ряда на алгебраические
дополнения параллельного ряда равна нулю.
3.Т.Лапласа.Свойства.
Теорема Лапласа
Пусть выбраны любые k строк матрицы A. Тогда определитель матрицы A равен сумме всевозможных произведений миноров k-го порядка, расположенных в этих строках, на их алгебраические дополнения.
Следствие:1 Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.
Пусть A = (aij) — квадратная матрица размера . Пусть также задан некоторый номер строки i либо номер столбца j матрицы A. Тогда определитель A может быть вычислен по следующим формулам:
Разложение
по i-строке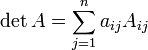
![]()
Разложение по j-строке
2. Сумма произведений всех элементов некоторой строки (столбца) матрицы А на алгебраические дополнения соответствующих элементов любой другой строки (столбца) равна нулю
4 Обратные матрицы и способы их вычисления.
Обра́тная
ма́трица — такая матрица A−1, при
умножении на которую исходная матрица
A даёт в результате единичную матрицу
E:
![]()
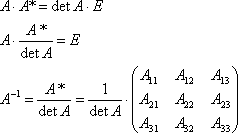
1.
![]()
2.
![]()
3.
![]()
5.Решение матричных уравнений.
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например,
чтобы найти матрицу
![]() из уравнения
из уравнения
![]() , необходимо умножить это уравнение на
, необходимо умножить это уравнение на
![]() слева.
слева.
Тогда:
![]()
Следовательно,
чтобы найти решение
уравнения
, нужно найти обратную матрицу
и умножить ее на матрицу
![]() ,
стоящие в правой части уравнения.
,
стоящие в правой части уравнения.
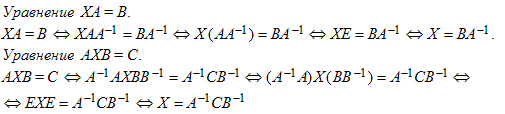
6.Система линейных алгебраических уравнений .Метод Крамера уравнений
Совокупность уравнений :
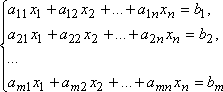
относительна неизвестных x1, x2, ..., xn-1, xn называется системой линейных алгебраических уравнений.
Числа aij — коэффициенты системы, bi— правые части системы i = 1, 2, ..., m; j = 1, 2, ..., n.
Совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, называется решением системы.
Система, имеющая хотя бы одно решение, называется совместной. Система, у которой нет решений, называется несовместной.
Каждое решение совместной системы называется частным решением. Совокупность всех решений совместной системы называется общим решением.
Если среди правых частей bi системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.
Если все правые части системы равны нулю, то система называется однородной.
Система линейных уравнений может быть записана в матричной форме A·x = b:
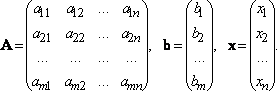
Здесь A — матрица системы, b — правая часть системы , x— искомое решение системы.
Иногда удобно записывать систему линейных уравнений в другой матричной форме:
A(1)x1 + A(2)x2 + ... + A(n)xn = b.
Здесь A(1), A(2), ... , A(n) — столбцы матрицы системы.

Матрица Ap называется расширенной матрицей системы.
Если исследуется неоднородная система A·x = b, b ≠ 0, то система A·x =0 называется приведенной однородной системой для системы A·x = b.
МЕТОД КРАМЕРА!
Пусть дана система линейных уравнений
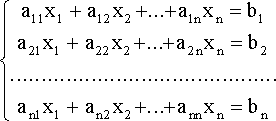
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка íx1 , x2 , ... , xn
ý - называется решением системы (1), если при подстановке этих чисел
вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij
ç, составленный из коэффициентов при неизвестных , называется
определителем системы (1). В зависимости от определителя системы (1) различают
следующие случаи.
a). Если D¹0, то система (1) имеет единственное решение, которое может
быть найдено по формулам Крамера : x1=
, где
определитель n-го порядка Di ( i=1,2,...,n) получается из
определителя системы путем замены i-го столбца свободными членами b1
, b2 ,..., bn.
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо
несовместна ,т.е. решений нет.
