- •6. Понятие волн де Бройля...
- •9. Опыты Резерфорда Ядерная модель атома.
- •13. Постулаты квантовой механики.
- •17.Одномерная яма конечной глубины.
- •18. Прямоугольный потенциальный барьер.
- •19. Контактная разность потенциалов.Холодная эмиссия электронов из металлов, альфа распад.
- •23. Атом водорода, собственное значение и собственная ф-я угловой части ур-я Шредингера
- •24. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
- •24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
- •25. Маг и мех моменты электрона. Правило квантования.
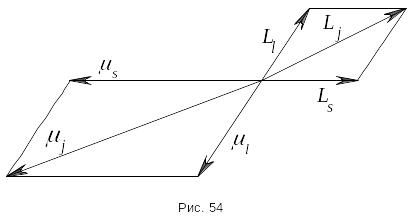
- •26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
- •27.Эффект Зеемана.
- •29. Эффект Пашена – Бака.
- •32. Рентгеновские спектры.
24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
Экспериментальные факты. При анализе спектров щелочных металлов с помощью спектроскопических приборов высокой разрешающей силы обнаруживается, что каждая из линий излучения в действительности расщеплена на две линии, т. е. является дублетом.
Расщепление имеет следующие ярко выраженные закономерности:
а) у линий главной серии расщепление не является постоянным, а меняется от линии к линии;
б) у линий диффузной серии расщепление одинаково у всех линий;
в) у линий резкой серии расщепление также одинаково.
Наличие расщепления у линий показывает, что энергия уровней зависит не только от главного квантового n и орбитального l чисел, но и от некоторой дополнительной величины, которая несколько изменяет энергию уровней. Почему возникает дублетный характер линий в спектрах щелочных металлов?
Из-за спин-орбитального взаимодействия.
Расщепление уровня энергии, вызванное спин-орбитальным взаимодействием, называется тонким расщеплением, а структура спектральных линий, соответствующая переходам между расщеплёнными уровнями, называется тонкой структурой (расстояние между ними на 2 порядка меньше расстояния между уровнями).
Спин электрона. Спин – число, характеризующее внутреннюю степень свободы частицы (электрона).
s=1/2, sz=-1/2, ½
Спин-орбитальное взаимодействие – взаимодействие магнитного момента электрона с внутриатомным магнитным полем.
Электрон обладает собственным механическим моментом импульса, называемым спином электрона. Кроме спина электрон также обладает магнитным моментом.


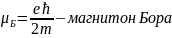
Для количественного согласия теории с экспериментом механический момент импульса электрона- спин-по модулю должен быть равен
|Ls|
= ћ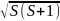 (S=
1/2), (34.2)
(S=
1/2), (34.2)
где h - постоянная Планка. Поскольку спин есть момент импульса, формула (34.2) записана в полной аналогии с для орбитального момента импульса частицы. Проекция спина на избранное направление может иметь лишь два значения:
LSZ = msћ (ms = 1/2, ms = -1/2). (34.3)
25. Маг и мех моменты электрона. Правило квантования.
Итак, электрон обладает в атоме четырьмя моментами:
Механическим (орбитальным и спиновым);
М
 агнитным
(орбитальным и спиновым).
агнитным
(орбитальным и спиновым).
Полный
механический момент импульса электрона
является векторной суммой орбитального
механического момента и спинового
механического момента:
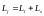 .
Так как модули каждого момента всегда
квантуются:
.
Так как модули каждого момента всегда
квантуются:
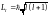 ,
,
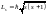 то
и их сумма должна квантоваться:
то
и их сумма должна квантоваться:
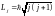 ,
где
,
где
 – квантовое число полного механического
момента электрона. Найдём его. Рассмотрим
значения проекций на ось Z:
– квантовое число полного механического
момента электрона. Найдём его. Рассмотрим
значения проекций на ось Z:
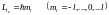 –
–
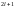 значение;
значение;
 .
Тогда
.
Тогда
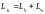 ;
;
 ,
где
,
где
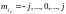 –
–
 значение. Так как
значение. Так как
 ,
то тогда
,
то тогда
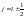 .
Определим угол между орбитальным и
спиновым моментами электрона. Так как
.
Определим угол между орбитальным и
спиновым моментами электрона. Так как
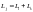 ,
то, возводя это выражение в квадрат,
получим:
,
то, возводя это выражение в квадрат,
получим:
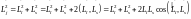 .
Отсюда
.
Отсюда
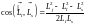 ,
или
,
или
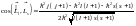 .
Так как возможно лишь
.
Так как возможно лишь
 – 2 состояния, то существует 2 возможных
угла между орбитальным и спиновым
моментами. Так как направление момента
относительно любой оси не определено,
то возникает вопрос, что же понимать
под углом между этими моментами? Смысл
данного угла в том, что в отсутствии
внешних сил полный момент импульса
сохраняется, орбитальный и спиновой
моменты прецессируют вокруг полного
момента, а их проекции на направление
полного момента имеют вполне определённые
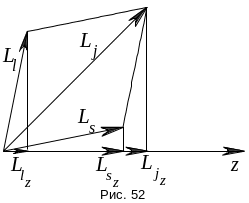
значения (рис. 53).
– 2 состояния, то существует 2 возможных
угла между орбитальным и спиновым
моментами. Так как направление момента
относительно любой оси не определено,
то возникает вопрос, что же понимать
под углом между этими моментами? Смысл
данного угла в том, что в отсутствии
внешних сил полный момент импульса
сохраняется, орбитальный и спиновой
моменты прецессируют вокруг полного
момента, а их проекции на направление
полного момента имеют вполне определённые
значения (рис. 53).
Полный
магнитный момент электрона равен сумме
векторов орбитального магнитного
момента и спинового магнитного момента:
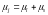 .
Так как
.
Так как
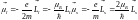 .
Таким образом, гиромагнитное отношения
для механических и магнитных моментов
различны. Поэтому полный механический
и полный магнитный момент не коллинеарны.
.
Таким образом, гиромагнитное отношения
для механических и магнитных моментов
различны. Поэтому полный механический
и полный магнитный момент не коллинеарны.