- •6. Понятие волн де Бройля...
- •9. Опыты Резерфорда Ядерная модель атома.
- •13. Постулаты квантовой механики.
- •17.Одномерная яма конечной глубины.
- •18. Прямоугольный потенциальный барьер.
- •19. Контактная разность потенциалов.Холодная эмиссия электронов из металлов, альфа распад.
- •23. Атом водорода, собственное значение и собственная ф-я угловой части ур-я Шредингера
- •24. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
- •24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
- •25. Маг и мех моменты электрона. Правило квантования.
- •26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
- •27.Эффект Зеемана.
- •29. Эффект Пашена – Бака.
- •32. Рентгеновские спектры.
23. Атом водорода, собственное значение и собственная ф-я угловой части ур-я Шредингера
Р/м
движение эл-на в центрально-симметричном
кулоновском поле ядра. Ур-е Шр-ра для
частицы в центрально-симметричном поле:
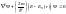 .
Будем р/м движение частицы в сферической
системе координат.
.
Будем р/м движение частицы в сферической
системе координат.
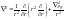 (1), где
(1), где
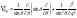 (1). Решение уравнения Шредингера будем
искать в виде:
(1). Решение уравнения Шредингера будем
искать в виде:
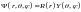 .
Подст-я реш в ур Шредингера:
.
Подст-я реш в ур Шредингера:

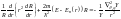 .
Так как обе части этого уравнения входят
независимые переменные и эти части
равны, то мы должны положить
.
Так как обе части этого уравнения входят
независимые переменные и эти части
равны, то мы должны положить
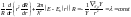 .
Т.о, это ур распадается на 2:
.
Т.о, это ур распадается на 2:
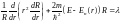 (2) и
(2) и
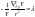 (3). Рассмотрим сначала решение ур
(3). Распишем лапласиан, связанный с
поворотом тела в прост-ве:
(3). Рассмотрим сначала решение ур
(3). Распишем лапласиан, связанный с
поворотом тела в прост-ве:
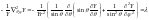 .
.
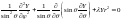 .
Так как
.
Так как
 не зависит ни от
не зависит ни от
 ,
ни от
,
ни от
 ,
то
,
то
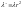 =const
Тогда
=const
Тогда
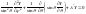 .
Будем искать его решение в виде:
.
Будем искать его решение в виде:
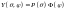
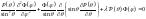 Разделим
на
Разделим
на
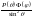 :
:
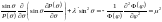 ,
где
,
где
 – константа разделения. Разобьём это
ур на 2 части:
– константа разделения. Разобьём это
ур на 2 части:
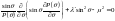 и
и
 ,
,
 .
Запишем систему
.
Запишем систему
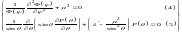
Решение
первого уравнения данной системы имеет
вид:
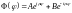 .
Из требования однозначности решения
следует, что
.
Из требования однозначности решения
следует, что
 должно быть любым положительным или
отрицательным числом. Поэтому все
собственные функции дифференциального
уравнения (4) могут быть представлены
формулой:
должно быть любым положительным или
отрицательным числом. Поэтому все
собственные функции дифференциального
уравнения (4) могут быть представлены
формулой:
 ,
где m=0,+-1,+-2.
Постоянная C
находится из условия нормировки и равна
,
где m=0,+-1,+-2.
Постоянная C
находится из условия нормировки и равна
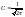 .
Т.образом,
.
Т.образом,
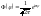 .
Решая уравнение (5), перейдём к новым
координатам:
.
Решая уравнение (5), перейдём к новым
координатам:
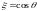 .
Тогда
.
Тогда
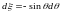 и
и
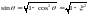 ;
dθ=-dξ/√(1-ξ2).
С учётом последних преобразований
перепишем уравнение (5):
;
dθ=-dξ/√(1-ξ2).
С учётом последних преобразований
перепишем уравнение (5):
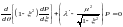 .
Чтобы привести данное уравнение к
стандартному виду введём обозначение:
.
Чтобы привести данное уравнение к
стандартному виду введём обозначение:
 ,
где l
– неотрицательное целое число. Тогда
решением данного уравнения будет
присоединённый полином Лежандра:
,
где l
– неотрицательное целое число. Тогда
решением данного уравнения будет
присоединённый полином Лежандра:
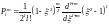 .
Причём, при заданном l,
m
может принимать только 2l+1
значение:
.
Причём, при заданном l,
m
может принимать только 2l+1
значение:
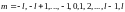 .
Волновая функция должна удовлетворять
условию нормировки:
.
Волновая функция должна удовлетворять
условию нормировки:
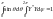 ;
;
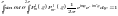 .
Так как
.
Так как
 и
связаны однозначно, то мы можем переписать
последний интеграл в виде:
и
связаны однозначно, то мы можем переписать
последний интеграл в виде:
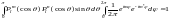 .
Выражение, стоящее под внутренним
интегралом, не зависит от
,
поэтому мы можем вычислять каждый
интеграл по отдельности и полученные
значения перемножить. Известно, что
.
Выражение, стоящее под внутренним
интегралом, не зависит от
,
поэтому мы можем вычислять каждый
интеграл по отдельности и полученные
значения перемножить. Известно, что
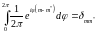 ,
где
,
где
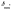 – символ Кронекера. Второй интеграл
даёт значение
– символ Кронекера. Второй интеграл
даёт значение
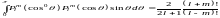 .
Собственная функция уравнения (5)
запишется в виде:
.
Собственная функция уравнения (5)
запишется в виде:
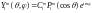 .
Тогда с помощью условия нормировки, мы
можем записать:
.
Тогда с помощью условия нормировки, мы
можем записать:
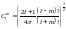 .
.
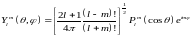 .
Мы получили угловую функцию, описывающую
движение частиц в центрально –
симметричном поле.
.
Мы получили угловую функцию, описывающую
движение частиц в центрально –
симметричном поле.
24. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
Рассмотрим
потенциальную энергию частицы:
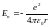 .
Решим уравн Шредингера для потенциальной
составляющей:
.
Решим уравн Шредингера для потенциальной
составляющей:
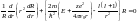 .
Введём следующие обозначения:
.
Введём следующие обозначения: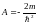 ;
;
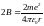 .
Замена переменных:
.
Замена переменных: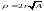 ,
, ;
; .
Тогда уравнение примет вид:
.
Тогда уравнение примет вид:
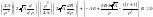
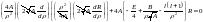
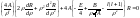
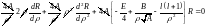
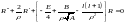 (1).
(1).
1)Р/м
сначала асимптотическое решение при
p→∞.
Тогда(1) преобр к виду:
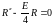 .
Решением его будет
.
Решением его будет .
Чтобы решен было ограничено на
бесконечности, необходимо положить
.
Чтобы решен было ограничено на
бесконечности, необходимо положить
 ;
;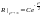 .
.
2)Теперь
рассмотрим ассимптотику при p→0: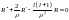 .
Решение будем искать ввиде:
.
Решение будем искать ввиде: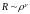 :
: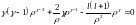 ,
,
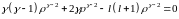 ,
,
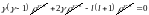 ;
;
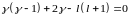 .
Мы получили уравнение относительно
.
Мы получили уравнение относительно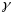 :
: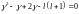 ,
,
 .
.
 .
Если
.
Если
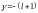 ,
то
,
то
 .
При p→∞,
p→0.
Поэтому данное
.
При p→∞,
p→0.
Поэтому данное
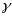 придётся отбросить. Т.о, остаётся решение:
придётся отбросить. Т.о, остаётся решение:
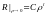 .
.
Решение
для радиальной составляющей волновой
функции мы будем искать в виде:
 .
Здесь ν(p)
– некот функция, которая определяет
поведение R
в промежутке от 0 до бескон. Подставляем
данный вид реш-я в (1):
.
Здесь ν(p)
– некот функция, которая определяет
поведение R
в промежутке от 0 до бескон. Подставляем
данный вид реш-я в (1):
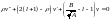 (2). Введём ограничен на функцию
(2). Введём ограничен на функцию
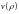 :
она не должна на бескон расти быстрее,
чем
:
она не должна на бескон расти быстрее,
чем
 ,
а в 0 должна либо обращаться в 0, либо
быть const,
,
а в 0 должна либо обращаться в 0, либо
быть const,![]() .
Подставим в (2):
.
Подставим в (2):
![]()
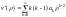
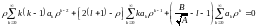
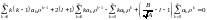
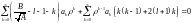 .
.
Д![]() анный
многочлен будет равен нулю только в том
случае, когда коэффициенты при каждой
степени p
будут равны нулю:
анный
многочлен будет равен нулю только в том
случае, когда коэффициенты при каждой
степени p
будут равны нулю:
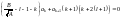 .
Данное соотношение даёт рекуррентную
формулу
.
Данное соотношение даёт рекуррентную
формулу
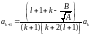 .
Оценим коэффициенты ak
при k→∞:
.
Оценим коэффициенты ak
при k→∞:
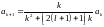 ,
,
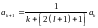
 .
Т.о,
.
Т.о,
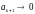 и
и
 .
Тогда при каком-нибудь малом значении
.
Тогда при каком-нибудь малом значении
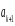 многочлен можно оборвать:
многочлен можно оборвать:
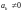 ,
а
,
а
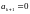 .
Данное услов будет выполнено, если
коэффициент при
.
Данное услов будет выполнено, если
коэффициент при
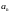 будет равен нулю:
будет равен нулю:
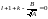 ,
,
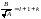 ;.
;.
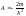 ,
,
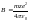 .
.
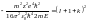 .
.
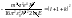 ,
,
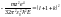 .
Из этой формулы следует, что энергия
зависит от l
и k.
Введём следующее обозначение: l+k+1=n.
Тогда
, где n=1,2,...
Таким образом, решая уравнение Шредингера,
мы нашли энергии водородоподобного
атома, то есть нашли собственные значения
оператора Гамильтона.
.
Из этой формулы следует, что энергия
зависит от l
и k.
Введём следующее обозначение: l+k+1=n.
Тогда
, где n=1,2,...
Таким образом, решая уравнение Шредингера,
мы нашли энергии водородоподобного
атома, то есть нашли собственные значения
оператора Гамильтона.
22. Собственные значения энергии щелочных металловЩелочные металлы в периодической системе Менделеева следуют за благородными газами: литий следует за гелием, натрий-на неоном.Щелочные металлы одновалентны и их сравнительно легко ионизировать.Щелочные атомы являются водородоподобными атомами, однако не полностью. Дело в том, что внешний электрон несколько деформирует оболочку первых Z — I электронов и несколько искажает их поле. Поэтому потенциальную энергию валентного электрона можно представить в виде
Eп(r)=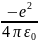 (
(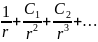 )
(33.1)
)
(33.1)
где
-
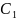 е2/(
е2/(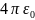 r2),
- С2
е2/(
r3)
-поправки, учитывающие отличие поля
атомов щелочных металлов от поля атома
водорода. В вычислениях мы ограничимся
учетом лишь первой поправки -
е2/(
r2)
получаем
r2),
- С2
е2/(
r3)
-поправки, учитывающие отличие поля
атомов щелочных металлов от поля атома
водорода. В вычислениях мы ограничимся
учетом лишь первой поправки -
е2/(
r2)
получаем
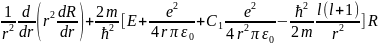 =
0. (33.2)
=
0. (33.2)
Переписав это уравнение следующим образом:
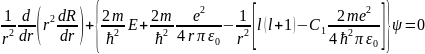 (33.3)
(33.3)
если положить
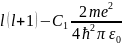 =
l'(l'
+ 1), (33.4)
=
l'(l'
+ 1), (33.4)
причем во все последующие вычисления вместо величины l войдет величина l', определяемая формулой (33.4). Решение квадратного уравнения (33.4):
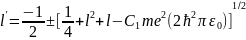 (33.5)
(33.5)
Отрицательные значения l' должны быть отброшены, поскольку они приводят к бесконечности волновой функции в нуле. Окончательно выражение (33.5) для l' может быть представлено в виде
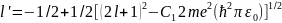 (33.6)
(33.6)
Если
= 0, то
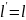 .
Член, содержащий
,
учитывает поправку на искажение поля.
Если оно мало, этот член также мал
.
Член, содержащий
,
учитывает поправку на искажение поля.
Если оно мало, этот член также мал
Тогда
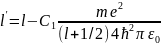 (33.8)
(33.8)
Из формулы (33.1) видно, что имеет размерность длины. Чтобы
второй член был малым по сравнению с первым, надо, чтобы (C1/ r0)«1, где г0- расстояние от ядра до ближайшего электрона. Учитывая, что в формуле (33.8) те2/(4пг0 ћ2) = = 1 /а0, где а0~ радиус первой боров- ской орбиты, мы убеждаемся, что поправочный член в (33.8) действительно мал. Главное квантовое число заменяется числом
n'
= l'
+ k+1
= l
+ k+1-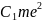 [
[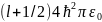 ]
-1
=
п + σ(l),
(33.9а)
]
-1
=
п + σ(l),
(33.9а)
где
σ(l)= - С1 те2/[ ] (33.96)
а формула для уровней энергии
 33
10)
33
10)
в которой для Е введено два индекса, поскольку теперь энергия зависит не только от главного квантового числа и, но и от орбитального квантового числа /.
Зависимость энергии от орбитального квантового числа составляет принципиальное отличие уровней энергии атомов щелочных металлов от уровней энергии атома водорода.
23. спектральные серии щелочных атомов, правила отбора.
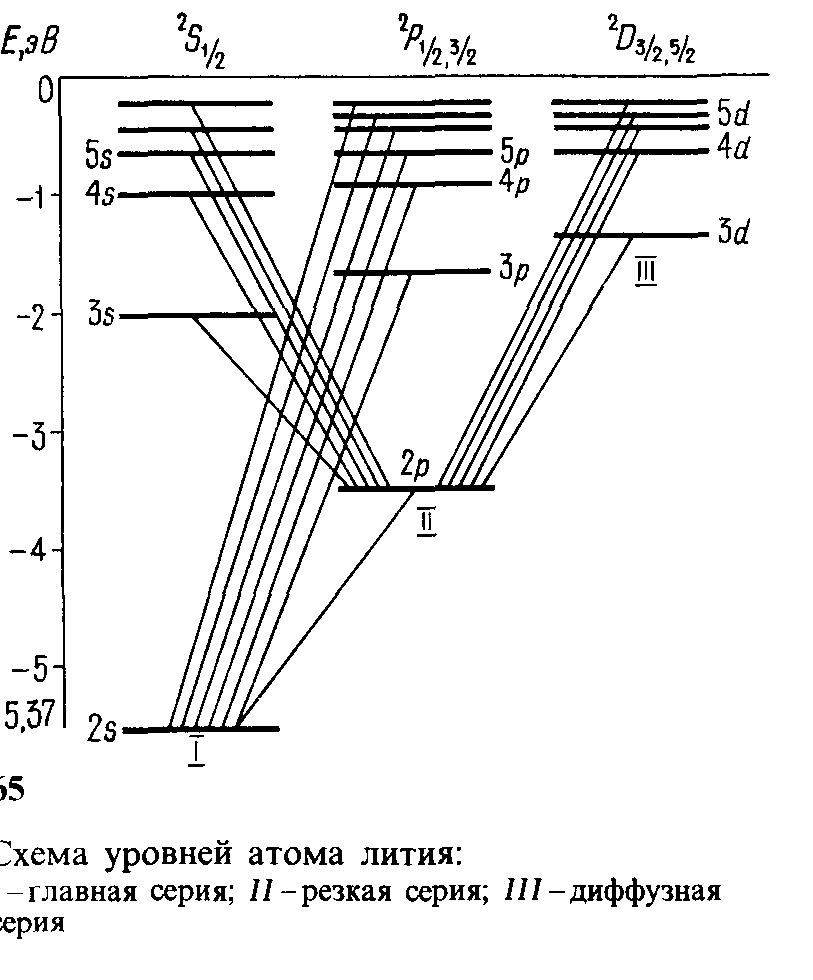
Спектры испускания атомов щелочных металлов, подобно спектру водорода, состоят из нескольких серий линий. Наиболее интенсивные из них получили названия: главная, резкая, диффузная и основная (или серия Бергмана). Эти названия имеют следующее происхождение. Главная серия названа так потому, что наблюдается и при поглощении. Следовательно, она соответствует переходам атома в основное состояние. Ее частоты условно обозначены в виде
w = 2S — тр (m = 2, 3, 4,...), (33.13)
т. е. частота со излучается в результате переходов электрона из состояний тр (т = 2, 3, 4,...) в состояние 2s.
В спектре атома лития имеются кроме главной и другие серии. Важнейшие из них следующие.
Первая побочная (или диффузная) серия. Частоты этой серии
w = 2p-md (m = 3,4,5,...). (33.14) Серия называется диффузной потому, что ее линии несколько размыты, не очень резки. Причина такой диффуз- ности линий объяснена ниже.
Вторая побочная (или резкая) серия. Частоты этой серии
w = 2 p-ms (m = 3,4,5,...). (33.15)
Резкая и диффузная серии состоят соответственно из резких и размытых (диффузных) линий. Серия Бергмана была названа основной (фундаментальной) за свое сходство с сериями водорода.
Следующая серия, получающаяся в результате переходов электрона из f-состояний в 3 d-состояние, лежит в инфракрасной части спектра.
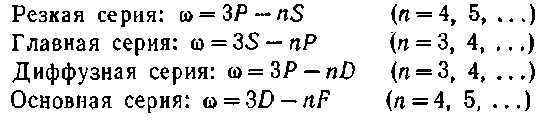
Правила отбора. Излучение происходит в результате перехода оптического электрона с одного энергетического уровня на другой. Однако не все переходы возможны. Возможными являются лишь переходы, разрешенные правилами отбора, которые совпадают с правилами отбора для одноэлектронного атома
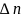 -любое
число,
-любое
число,
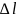 =
= 1,
(33.11) т. е.
1,
(33.11) т. е.
главное квантовое число может изменяться на любое значение, а орбитальное квантовое число-лишь на единицу.
Это означает, что возможны переходы лишь между соседними по L уровнями, т.е. между s- и p-состоя- ниями, между р- и d-состояниями, между d- и f-состояниями и т. д. (см. рис. 65).