17.Одномерная яма конечной глубины.

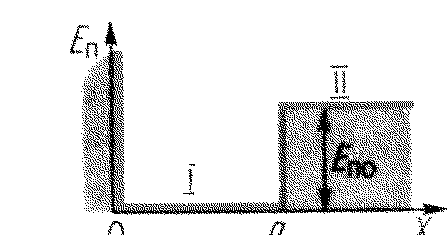
Предполагается (рис. 56), что при х < 0 потенциальная энергия обра­щается в бесконечность. Значит, ча­стица не может проникнуть в область х < 0 и, следовательно, в этой области волновая функция равна нулю. По­этому достаточно найти волновую функцию в областях lull при х > 0, заметив, что в точке х = 0 из-за не­прерывности волновая функция обра­щается в нуль.

Уравнение Шредингера в областях I (0 < х < а) и II (а < х <∞) имеет вид

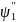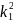
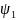1. + = 0, =2тЕ/ћ²,

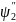2. + (2т/ћ²)(Е - Е_п0)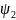 = 0. (26.10)

Случай Е > Е_п0. Уравнение Шредин­гера в области II

(II) + = 0, =(2т/ћ²)(Е - Е_п0) > 0,(26.11)

а в области I оно имеет вид (26.10; I). Решения для различных областей можно записать следующим образом:

1. = A_l sin(k₁x) + B_l cos(k₁x),(26.12)

2. = A₂sin[k₂(x-a)] + В₂cos[k₂(x-a)].

Из условия (0) = 0 следует, что В₁ = 0, а условия непрерывности функ­ции и ее производной

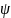₁(a) = ₂(a), (a) = (a) (26.13)

дают для коэффициентов А₂ и В₂ следующие выражения:

А₂ = (k₁A₁/k₂)cos(k₁a), В₂ = А₁sin(k₁a).(26.14)

Эти условия могут быть всегда удовлетворены. Поэтому в случае Е > Е_и0 спектр энергии непрерывен, частица при своем движении не лока­лизована в конечной области прост­ранства, ее движение инфинитно.

Случай Е < Е_п0. Уравнение Шре­дингера в области II имеет вид (II) +k² = 0 к²=(2т/ћ²)(Е_п0 - Е) > 0. (26.15)

В области I уравнение остается без изменения. Решения для областей I и II представляются функциями

1. = А₁sin (k₁x),(26.16)

2. = С₂е^-кх + D₂e^kx.

Так как волновая функция везде должна быть конечной, а е^кх при х->∞неограниченно возрастает, то D₂ в формуле (26.16; II) необходимо принять равным нулю.

Условия сшивания (26.13) в рас­сматриваемом случае:

А₁sin(k₁a) = С₂ехр(-ка),(26.17)

A_lk₁cos(k₂a) = -кС₂ехр(-ка).

Разделив почленно второе уравнение на первое, получим условие квантова­ния энергии:

k₁ctg(k₁a) = -к. (26.18)

Для графического решения этого урав­нения удобно сделать следующие пре­образования:

sin (k₁a) = [1 + ctg²k₁a)]^-1/2 = [1+(k/k₁)2] ^-1/2 =[1+(Е_п0-E)/E]^-1/2 = (Е/Е_п0)^1/2.

Но 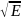= ћk₁/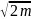

и, следовательно, уравнение (26.18) принимает вид

sinу= (ћ/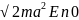 )у(y=k₁a)• (26.19)

Это уравнение решается с помощью построения, указанного на рис. 57. В качестве решений берутся не все пересечения прямой z = (ћy/ ) с синусоидой z = siny, а лишь те, ко­торые согласуются со знаком в урав­нении (26.18), т. е. точки пересечения в четных четвертях. Этим значениям у_п, которых имеется конечное число, соответствуют энергии

Е_n = ћ²y²/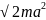 (26.20)

Таким образом, в потенциальной яме с конечной глу­биной имеется конечное число собст­венных значений энергии.

Волновая функция при х > а, согласно (26.16; II), имеет вид

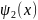= С₂е^-кх (26.21)

18. Прямоугольный потенциальный барьер.

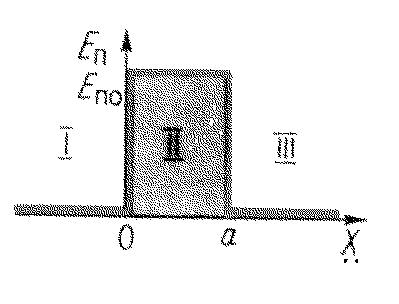
Рассмотрим для определенно­сти случай Е < Е_п0 и найдем коэф­фициенты D-коэф.прохождения и R-коэф.отражения. Уравнение Шредин­гера в различных областях имеет сле­дующий вид:

1. + = 0, =2тЕ/ћ²=к²,

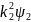2. + = 0, =(2т/ћ²)(Е_п0-E)>0

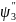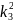
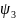3. + = 0, =2тЕ/ћ²=к² (29.2)

где штрихами обозначены производ­ные по х.

В области I имеются как падаю­щая, так и отраженная волны:

= A₁e^ikx + B_le^-ikx, (29.3)

а в области III- только прошедшая волна, движущаяся в положительном направлении оси X:

= А₃е^iк(х-а). (29.4)

В области II общее решение имеет, очевидно, вид

= А₂ + В₂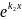 (29.5)

Плотность потоков падающих, отра­женных и прошедших частиц равна соответственно

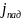= (ћк/т) |A₁|²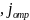 = - (ћк/т)|В₁|²,

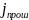= (ћk/т)|А₃|²,

По определению,

D = | |/| | = |A₃|²/|A₁|² (29.6)

R= |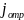 |/| | = |B₁|²/|A₁|² (29.7)

Из условий непрерывности волно­вой функции и ее производной в точ­ках x = 0, х = а находим следующие соотношения между коэффициентами:

А₁ + В₁ = А₂ + В₂, (29.8а)

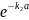А₂ + В₂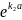 = А₃. (29.8б)

ik(A₁-B_l) = k₂(B₂-A₂), (29.8в)

k₂(В₂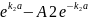 )= ikA₃ (29.8г)

Из (29.8г), (29.8б) следует, что

A₂=¹/₂(1-in) A₃,

В₂=¹/₂(l+in) А₃.

Здесь n = k/k₂ = [E/(Е_п0 - Е) ^1/2.

Так как |1 – in|= |1 + in |, то из последних двух уравнений следует, что |А₂| »|В₂|. Поэтому можно поло­жить В₂ = 0. Решая уравнения (29.8), находим

А₁₌(1-in)(i + п) А₃/(2п),

B_l=(1-in)(n-i) А₃/(4п),.

Отсюда для коэффициента прохожде­ния получаем выражение

D = |A₃|²/|A₁|²=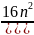 *ехр (-2 к₂а) = ехр {-[8т(Е_п0 - Е)-]^1/2а/ћ}. (29.9)

Коэффициент прохождения не слиш­ком мал тогда, когда

[8т(Е_п0 - Е)]-^1/2а/ћ≤1

Для электрона (т= 9,1 • 10^-31кг)

a≤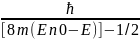 ͌ 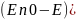^-1/2

Если, например, Е_п0 — Е = 1 эВ = 1,6-10 Дж, то коэффициент про­хождения отличен от нуля при а «10~^1Ом. В макроскопических явле­ниях туннельный эффект не играет существенной роли.

** Потенциальным барьером называется область пространства, где величина по­тенциальной энергии больше, чем в окру­жающих областях пространства. Туннельным эффектом называется про­никновение частицы через потенциаль­ный барьер. При туннельном эффекте в области потенциального барьера наруша­ется закон сохранения энергии.