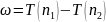- •6. Понятие волн де Бройля...
- •9. Опыты Резерфорда Ядерная модель атома.
- •13. Постулаты квантовой механики.
- •17.Одномерная яма конечной глубины.
- •18. Прямоугольный потенциальный барьер.
- •19. Контактная разность потенциалов.Холодная эмиссия электронов из металлов, альфа распад.
- •23. Атом водорода, собственное значение и собственная ф-я угловой части ур-я Шредингера
- •24. Атом водорода, собственное значение и собственная ф-я радиальной части ур-я Шредингера
- •24. Дублетный характер спектров щелочных металлов. Спин эл-на, спин-орбитальное взаимодействие.
- •25. Маг и мех моменты электрона. Правило квантования.
- •26. Маг и мех момент атома. Векторная модель атома. Jj и l-s связь…
- •27.Эффект Зеемана.
- •29. Эффект Пашена – Бака.
- •32. Рентгеновские спектры.
1. Фотоэффект. Ур-е Эйнштейна для фотоэффекта. Одним из явлений, в которых обнаруживается корпускулярная природа электромагнитных волн является фотоэффект. Под фотоэффектом понимают изменение состояния электронов в веществе под действием света (эл.маг излучения). Различают внутренний и на внешний фотоэффекты. При внутреннем фотоэффекте электроны с поверхности вещества не вырываются. Внутренним фотоэффектом называется перераспределение электронов по энергетическим состояниям в твердых и жидких полупроводниках и диэлектриках, происходящее под действием излучений.Внешний фотоэффект состоит в вырывании электронов с поверхности вещества под действием электромагнитного излучения. Законы внешнего фотоэффекта: 1.
Существует граничная частота света
2.
Электроны покидают поверхность катода
с энергиями от нуля до максимальной
3. При фиксированной частоте излучения число электронов, выбитых из катода в единицу времени, прямо пропорционально плотности светового потока энергии. Объяснение фотоэффекту дал А.Эйнштейн, который предположил, что поток энергии световой волны не является непрерывным, а представляет собой поток дискретных порций, называемых квантами или фотонами. При
этом согласно гипотезе М. Планка,
энергия кванта света с частотой
Равна
Фотоны столкнувшись с электроном в металле, передает всю свою энергию. Если энергия, переданная фотоном, достаточна для преодоления сил, удерживающих электрон в металле, то электрон вылетит из металла. Закон сохранения для этого процесса:
Это соотношение называется ур-ем Эйнштейна для фотоэффекта и оно полностью объясняет все законы фотоэффекта.
|
2. Эффект Комптона Волновая теория, удовлетворительно объясняющая эффект рассеяния длинноволнового излучения, оказывается несостоятельной при описании рассеяния рентгеновских и гамма-лучей. Это относится, в частности, к объяснению экспериментального обнаруженного факта появления в спектре рассеянного излучения компонент, отсутствующих в спектре падающего излучения. Упругое рассеяние на свободных (или слабо связанных) электронах сопровождающееся увеличением длины волны, называется эффектом Комптона. (Рис.) Комптон
сделал вывод на основании экспериментальных
данных, что сдвиг длины волны
Р-им упругое столкновение двух частиц: светового кванта и электрона. Пусть
до взаимодействия электрон неподвижен.
Фотон с импульсом
Сложим импульс по правилу параллелограмма. Применим теорему косинусов:
Возведем (3) в квадрат:
Получим:
Или
Вычисления
показывают, что
|
4.Дифракция рентгеновских частиц в кристаллах. Метод исследования дифракции:способы Лауэ, Брегга, Дебая_Шерера Методы наблюдения дифракции волн на кристаллах.
d-расстояние между плоскостями. Известны три способа наблюдения дифракции волн на кристаллах. 1. Способ Лауэ. Монокристалл облучается рентгеновским излучением с непрерывным спектром. Каждая из систем параллельных поверхностей, проведенных через узлы монокристалла, отражает в соответствующем направлении определенную длину волны. Интенсивность отраженного луча будет заметной лишь в том случае, когда атомы в отражающих плоскостях расположены достаточно плотно. Поэтому практически будет наблюдаться отражение лишь от небольшого числа систем плоскостей. Если на пути лучей, отраженных от различных систем плоскостей, поставить фотопластинку, то на ней получается система пятен - лау-эграмма. Зная геометрию опыта, можно установить соотношение между лауэграммой, структурой кристалла и длинами волн. 2. Способ Брэгга. В этом случае кристалл облучается монохроматическим рентгеновским излучением. Исследуется отражение от определенной системы параллельных атомных плоскостей при вращении монокристалла. В соответствии с формулой (1) отражение происходит лишь при некоторых углах скольжения. Измерив угол и знак X, по формуле (1) можно рассчитать d для системы параллельных плоскостей, от которой происходит отражение. Вместо вращения кристалла при практическом осуществлении опыта часто бывает удобнее изменять направление падающих лучей, оставляя кристалл неподвижным. В принципиальном отношении это ничего нового по сравнению с вращением кристалла не содержит. 3. Способ Дебая - Шерера. Монокристаллы достаточно больших размеров получать трудно. Гораздо проще получить порошше, который состоит из маленьких монокристаллов, ориентированных беспорядочно. Кроме того, часто возникает необходимость исследовать поликристаллы вместо монокристаллов по другим обстоятельствам. Для этого применяется способ Дебая - Шерера. Если данный поликристаллический порошок облучать монохроматическим рентгеновским излучением, то среди составляющих его монокристаллов всегда найдутся такие, ориентация которых относительно падающего пучка удовлетворяет условию Вульфа-Брэгга (1). Если в направлении падающего луча установить фотопластинку, то ввиду аксиальной симметрии отраженных лучей на пластинке они оставят след в виде кольца (рис. 29). Так как отражение одновременно происходит от разных систем поверхностей и имеются отражения различных порядков, т. е. при различных значениях т в формуле (1), то на фотопластинке наблюдается система колец. Зная геометрию опыта, длину волны и расположение колец, можно сделать заключение о структуре монокристаллов, а при известной структуре можно вычислить длину волны. Все три способа наблюдения дифракции волн на кристаллических структурах были успешно использованы для изучения дифракции рентгеновских лучей. Это позволило экспериментально доказать электромагнитную природу рентгеновского излучения и определить длину волны рентгеновского излучения, поскольку межатомные расстояния кристаллов можно оценить независимо от дифракции рентгеновских лучей, зная удельную массу и атомную массу. позволило установит что длины волн рентгеновского излучения имеют порядок размеров атомов и поэтому осуществить с ними опыт Юнга затруднительно.
|
5. Эффект Рамзауэра – Таунсенда. Рамзауэр исследовал (1921) упругое рассеяние электронов на атомах аргона при энергиях электрона от меньше чем одного до нескольких десятков электрон-вольт. частности аргона) для медленных электронов. Брался триод, в одной половине которого электроны не ускорялись, а в другой ускорялись. Трубку триода наполняли инертным газом (аргон). Электрон, попадая с раскалённой нити катода в пространство триода, движется по направлению к катоду и сталкивается с молекулой газа; при этом электрон рассеивается на ней. Поэтому, чем больше будет энергия электрона, тем больше шансов, что он пролетит без столкновения, то есть тем меньше вероятность рассеяния. Таким образом, с ростом ускоряющей разности потенциалов сила тока в цепи катод – анод должна возрастать. Графически зависимость между данными величинами можно представить так (см. рис. 17). Здесь зависимость P=P(E) есть зависимость вероятности рассеяния электрона от его энергии. Введём теперь в рассмотрение несколько новых величин, которые впоследствии помогут нам количественно описать эффект Рамзауэра.Одновременно аналогичные исследования проводились Таунсендом. Они измерили зависимость поперечных сечений упругого рассеяния электронов на молекулах газа в зависимости от энергии электрона. В результате этих исследований было обнаружено замечательное явление, получившее название эффекта Рамзауэра-Таунсенда. Оно состоит в следующем.
. Будем
считать частицу точечной. Пусть
электрон падает на площадь
При уменьшении энергии электрона от нескольких десятков электрон-вольт поперечное сечение его упругого рассеяния на аргоне растет, как это и предсказывается теорией. Затем при энергии электрона около 16 эВ поперечное сечение достигает максимума и при дальнейшем уменьшении энергии электрона уменьшается. При энергии электрона при- мерно 1 эВ поперечное сечение близко к нулю и затем начинает увеличиваться (рис. 33). Увеличение эффективного сечения с ростом энергии электрона и тем более почти полное исчезновение рассеяния вблизи энергии 1 эВ нельзя понять с точки зрения классических представлений, так как при этой энергии атомы аргона становятся как бы несуществующими для электронов и электроны пролетают сквозь них без столкновения. Эффект Рамзауэра – Таунсенда объясняется совершенно аналогично возникновению пятна Пуассона, если предположить, что электрон ведет себя как волна. Когда длина волны электрона имеет порядок диаметра атома, должна наблюдаться хорошо выраженная дифракция и за атомом возникает своеобразное «пятно Пуассона», т. е. электрон как бы проходит сквозь атом без отклонения и поперечное сечение его рассеяния на атоме близко к нулю.
|
6. Понятие волн де Бройля...
В 1927 г. Луи де Бройль высказал предположение, что каждой движущейся частицы, мы можем поставить в соответствие некоторую длину волны. Подобную волну назвали в последствии волной де Бройля. Установим связь между параметрами волны и движущейся частицы.
Для волны де Бройля, как и для любой другой электромагнитной волны, мы можем записать:
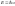 (1). С другой стороны, для импульса:
(1). С другой стороны, для импульса:
 ;
;
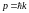
 ,
где
,
где
 -
волновой вектор. Но для волнового
вектора мы можем записать:
-
волновой вектор. Но для волнового
вектора мы можем записать:
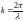 ,
т. о.
,
т. о.
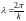 ;
;
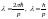 .
Из последней формулы следует выражение
для волны де Бройля:
.
Из последней формулы следует выражение
для волны де Бройля:
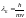 (2). Из этого выражения следует интересный
вывод, касающийся распределения
интенсивностей в опытах с дифракцией
электронов. Изменяя приложенную
разгоняющую разность потенциалов, мы
изменяем длину волны де Бройля. Когда
выполняется условие Вульфа – Брэгга,
возникает максимум.
(2). Из этого выражения следует интересный
вывод, касающийся распределения
интенсивностей в опытах с дифракцией
электронов. Изменяя приложенную
разгоняющую разность потенциалов, мы
изменяем длину волны де Бройля. Когда
выполняется условие Вульфа – Брэгга,
возникает максимум.Определим теперь фазовый вид волн де Бройля. Введём некоторые дополнительные определения. Фазовой скоростью называют скорость, Vф с которой перемещается в пространстве фаза
 плоской монохроматической волны
плоской монохроматической волны
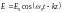 ,
где
,
где
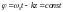 (3). Другими словами, фазовая скорость
– это скорость распространения точки
постоянной фазы волны. Найдём эту
скорость. Рассмотрим для этого выражение
(3). Это уравнение чисто геометрически
описывает плоскость, перпендикулярную
к оси
(3). Другими словами, фазовая скорость
– это скорость распространения точки
постоянной фазы волны. Найдём эту
скорость. Рассмотрим для этого выражение
(3). Это уравнение чисто геометрически
описывает плоскость, перпендикулярную
к оси
 ,
на которой постоянна фаза волны. Таким
образом, эта плоскость является как бы
траекторией движения точки постоянной
фазы. Поэтому, чтобы найти её скорость,
необходимо взять производную от (3) по
времени. Получим:
,
на которой постоянна фаза волны. Таким
образом, эта плоскость является как бы
траекторией движения точки постоянной
фазы. Поэтому, чтобы найти её скорость,
необходимо взять производную от (3) по
времени. Получим:
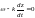 ,
так как производная от константы будет
ноль. Отсюда найдётся и фазовая скорость:
,
так как производная от константы будет
ноль. Отсюда найдётся и фазовая скорость:
 .
Это соотношение определяет как раз
фазовую скорость. Найдём некоторые
свойства фазовой скорости. Возвращаясь
к уравнениям
.
Это соотношение определяет как раз
фазовую скорость. Найдём некоторые
свойства фазовой скорости. Возвращаясь
к уравнениям
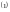 и
и
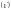 ,
выразим из них
,
выразим из них
 и
и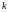 :
:
 и
и
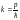 .
Основываясь на определении фазовой
скорости и полученных выражениях,
найдём другую форму записи для неё:
.
Основываясь на определении фазовой
скорости и полученных выражениях,
найдём другую форму записи для неё:
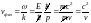 .
Здесь
.
Здесь
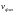 – фазовая скорость волны, соответствующей
частице;
– фазовая скорость волны, соответствующей
частице;
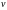 – скорость самой частицы;
– скорость самой частицы;
 – скорость света. Таким образом, как
видно из полученной формулы, фазовая
скорость будет больше скорости света,
однако никакого противоречия с теорией
относительности это не вызывает.
Очевидно, что фазовая скорость не
измерима в эксперименте. Измерить можно
лишь так называемую групповую скорость.
– скорость света. Таким образом, как
видно из полученной формулы, фазовая
скорость будет больше скорости света,
однако никакого противоречия с теорией
относительности это не вызывает.
Очевидно, что фазовая скорость не
измерима в эксперименте. Измерить можно
лишь так называемую групповую скорость.Групповой скоростью называют величину, приближённо характеризующую распространение негармонической волны (которая является суперпозицией группы гармонических волн). Если форма волны изменяется в результате дисперсии волн в среде не очень быстро, то можно рассматривать распространение негармонической волны как целого с групповой скоростью, отличной от фазовых скоростей её гармонических составляющих. Групповая скорость характеризует скорость переноса энергии волной. По определению для групповой скорости мы можем записать:
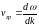 (отсюда сразу становится понятным
условие, ограничивающее скорость
изменения
(отсюда сразу становится понятным
условие, ограничивающее скорость
изменения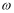 ).
Возвращаясь к соотношениям, полученным
для фазовой скорости, получим:
).
Возвращаясь к соотношениям, полученным
для фазовой скорости, получим:
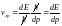 .
Таким образом,
.
Таким образом,
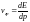 .
.Если волны распространяются в недиспрегирующей среде (фазовая скорость не зависит от частоты), то групповая скорость равна скорости движения частицы
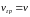 .
Тогда, вспоминая выражение для фазовой
скорости
.
Тогда, вспоминая выражение для фазовой
скорости
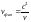 ,
мы можем записать:
,
мы можем записать:
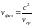 .
Из последней формулы следует:
.
Из последней формулы следует:
 .
.
Итак, мы установили,
как связаны свойства частиц и волн де
Бройля. Оценим теперь длину волны де
Бройля. В опытах Девисона – Джермера
ускоряющая разность потенциалов была:
100В. Тогда для энергии электрона имеем
выражение: Ee=eU.
С другой стороны, кинетическая энергия
электрона
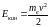 .
На основании закона сохранения энергии
необходимо положить
.
На основании закона сохранения энергии
необходимо положить
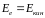 или
или
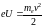 .
Так как импульс электрона будет
.
Так как импульс электрона будет
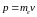 ,
то
,
то
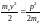 ,
то есть
,
то есть
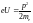 .
Отсюда
.
Отсюда
 .
Так как
.
Так как
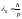 ,
то
,
то
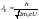 .
Для
электрона
.
Для
электрона
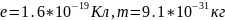
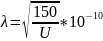 м
м
8. Опыт Франка-Герца. Атомные спектры. Любое излучение
электромагнитных волн осуществляется
телами. Если излучение дискретно, то
тело должно переходить с одного
дискретного уровня на другой. Опыты
Франка и Герца дали прямое доказательство
дискретности атомных состояний. Если
состояние атомных систем дискретно,
а кинетическую энергию свободных
электронов мы можем менять непрерывно,
то при взаимодействии электронов с
атомами, атомы могут поглощать энергию
лишь строго определёнными порциями.
В ходе опыта использовалась вакуумная
лампа (см. рис.25). В ней находились
накаливающийся катод, анод и две сетки,
которые соединялись между собой. На
сетку подавался ускоряющий потенциал
Отношение
энергии возбуждения атома к заряду
электрона называется потенциалом
ионизации:
Ионизацией
называется процесс отрыва электрона
от атома. Для определения потенциала
ионизации также используют установку,
изображённую на рисунке 25. Потенциал
ионизации определяется по формуле
Все спектры (испускания, поглощения) делятся на линейчатые, полосатые и сплошные. Чем проще структура вещества, тем разрежённей его спектр. С другой стороны, чем меньше электронов содержит вещество, тем проще его спектр. Линейчатые спектры характерны для атомов определённых веществ. Общая формула Бальмера для частот спектральных линий:
Формула
выражает собой закон, которому
подчиняется процесс лучеиспускания
водородоподобных атомов. Величины
Все излучаемые частоты могут быть представлены в виде комбинации спектральных термов. Это правило называется комбинационным принципом Ритца. |

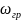 ,
ниже которой для данного материала
катода фотоэффект отсутствует,
независимо от плотности светового
потока энергии и продолжительности
облучения катода.
,
ниже которой для данного материала
катода фотоэффект отсутствует,
независимо от плотности светового
потока энергии и продолжительности
облучения катода.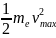 ,
которая не зависит от плотности
светового потока энергии и линейно
зависит от частоты.
,
которая не зависит от плотности
светового потока энергии и линейно
зависит от частоты.
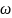
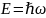 ,
где
,
где
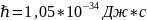 - постоянная
Планка.
- постоянная
Планка.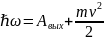
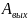 – работа
выхода.
– работа
выхода.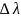 линейно пропорционален
линейно пропорционален
 ,
где
,
где
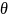 – угол рассеяния.. Мы можем записать:
– угол рассеяния.. Мы можем записать:
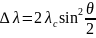 (1), где
(1), где
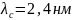 –комптоновская длина волны.
–комптоновская длина волны.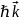 взаимодействует
с электроном мишени, рассеивается на
нём. Импульс фотона изменяется и
становится равным
взаимодействует
с электроном мишени, рассеивается на
нём. Импульс фотона изменяется и
становится равным
 .
Электрон также рассеивается и при
этом получает импульс
.
Электрон также рассеивается и при
этом получает импульс
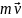 Таким
образом, мы можем записать законы
сохранения импульса и энергии:
Таким
образом, мы можем записать законы
сохранения импульса и энергии: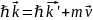 (2)
(2)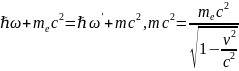 (3)
(3)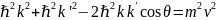
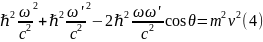
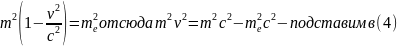
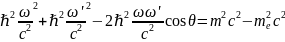
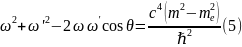
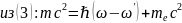
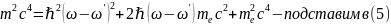
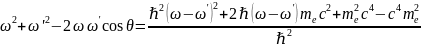

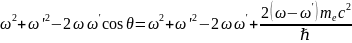
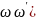

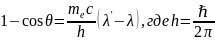
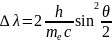
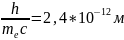 ,что в точности совпадает с комптоновской
постоянной. Таким образом из полученного
соотношения следует, что квантовая
теория хорошо объясняет эффект
Комптона, исходя из корпускулярных
свойств излучения.
,что в точности совпадает с комптоновской
постоянной. Таким образом из полученного
соотношения следует, что квантовая
теория хорошо объясняет эффект
Комптона, исходя из корпускулярных
свойств излучения.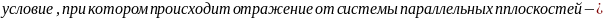
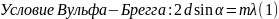
 объёма, в котором расположены молекулы
с концентрацией n0
(рис. 18). В сл:
ое толщиной
dx
в направлении движения электрона
находится число молекул n0dV=n0sdx.
объёма, в котором расположены молекулы
с концентрацией n0
(рис. 18). В сл:
ое толщиной
dx
в направлении движения электрона
находится число молекул n0dV=n0sdx.
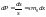
 ;
;
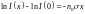 .
.
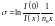 .
. .
Изменением его можно было плавно
изменять кинетическую энергию
электронов. На другую сетку подавался
задерживающий потенциал
.
Изменением его можно было плавно
изменять кинетическую энергию
электронов. На другую сетку подавался
задерживающий потенциал
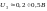 .
Электроны, ускоренные между сеткой и
катодом, попадали в свободное от полей
пространство. Наблюдалась ВАХ,
представленная на рисунке 26. Если
теперь наполнить трубку парами
(например, ртути) при пониженном
давлении, в пространстве между сетками
будут происходить столкновения
электронов с атомами ртути. Те, что не
потеряли энергию в результате подобных
столкновений, достигнут анода. Те же,
что энергию потеряли, анода не достигают.
Анодный ток убывает. ВАХ лампы в этом
случае представлена на рисунке 27.
Качественно её можно объяснить
следующим образом. Когда энергия
электрона меньше разности энергий
между энергетическими уровнями ртути,
то оно не отдаёт энергию атому при
столкновении. С увеличением ускоряющей
разности потенциалов энергия электронов
также возрастает. Когда разность
потенциалов достигает 4,9 эВ., электроны
при неупругом столкновении с атомами
ртути вблизи сетки отдадут им всю свою
энергию и уже не смогут преодолеть
запирающей разности потенциалов.
Следовательно, на анод могут попасть
лишь электроны не испытавшие неупругого
столкновения, и поэтому при разности
потенциалов 4,9В. сила тока начинает
уменьшаться. Когда разность потенциалов
достигает такого значения, что
достаточное число электронов после
неупругого столкновения смогут
приобрести энергию, необходимую для
преодоления задерживающего потенциала,
начинается новый рост силы тока. При
достижении разности потенциалов 9,8
В., электрон после одного неупругого
столкновения приходит к сетке с
энергией: 4,9 эВ., достаточной для второго
неупругого столкновения. При втором
неупругом столкновении электрон
теряет всю свою энергию и не достигает
анода. Поэтому сила тока начинает
уменьшаться (второй максимум на ВАХ).
Последующие максимумы объясняются
аналогично. Из опыта следует, что
разница в энергии основного состояния
атома ртути и ближайшего возбуждённого
состояния равна 4,9 эВ., что и доказывает
дискретность состояний атомных систем.
.
Электроны, ускоренные между сеткой и
катодом, попадали в свободное от полей
пространство. Наблюдалась ВАХ,
представленная на рисунке 26. Если
теперь наполнить трубку парами
(например, ртути) при пониженном
давлении, в пространстве между сетками
будут происходить столкновения
электронов с атомами ртути. Те, что не
потеряли энергию в результате подобных
столкновений, достигнут анода. Те же,
что энергию потеряли, анода не достигают.
Анодный ток убывает. ВАХ лампы в этом
случае представлена на рисунке 27.
Качественно её можно объяснить
следующим образом. Когда энергия
электрона меньше разности энергий
между энергетическими уровнями ртути,
то оно не отдаёт энергию атому при
столкновении. С увеличением ускоряющей
разности потенциалов энергия электронов
также возрастает. Когда разность
потенциалов достигает 4,9 эВ., электроны
при неупругом столкновении с атомами
ртути вблизи сетки отдадут им всю свою
энергию и уже не смогут преодолеть
запирающей разности потенциалов.
Следовательно, на анод могут попасть
лишь электроны не испытавшие неупругого
столкновения, и поэтому при разности
потенциалов 4,9В. сила тока начинает
уменьшаться. Когда разность потенциалов
достигает такого значения, что
достаточное число электронов после
неупругого столкновения смогут
приобрести энергию, необходимую для
преодоления задерживающего потенциала,
начинается новый рост силы тока. При
достижении разности потенциалов 9,8
В., электрон после одного неупругого
столкновения приходит к сетке с
энергией: 4,9 эВ., достаточной для второго
неупругого столкновения. При втором
неупругом столкновении электрон
теряет всю свою энергию и не достигает
анода. Поэтому сила тока начинает
уменьшаться (второй максимум на ВАХ).
Последующие максимумы объясняются
аналогично. Из опыта следует, что
разница в энергии основного состояния
атома ртути и ближайшего возбуждённого
состояния равна 4,9 эВ., что и доказывает
дискретность состояний атомных систем. .
Первый потенциал возбуждения
соответствует переходу атома с уровня
с наименьшей энергией на последующий
уровень.
.
Первый потенциал возбуждения
соответствует переходу атома с уровня
с наименьшей энергией на последующий
уровень.
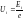 ,
где
,
где
 – работа выхода электрона из атома.
Для атома водорода ВАХ этого процесса
имеет вид, представленный на рисунке
28. Здесь измеряется ток, создаваемый
положительными ионами. Величина 13,6
В. называется потенциалом насыщения.
– работа выхода электрона из атома.
Для атома водорода ВАХ этого процесса
имеет вид, представленный на рисунке
28. Здесь измеряется ток, создаваемый
положительными ионами. Величина 13,6
В. называется потенциалом насыщения.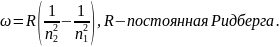
 называются спектральными термами.
Частота спектральных линий является
разностью ее нижнего и верхнего термов.
называются спектральными термами.
Частота спектральных линий является
разностью ее нижнего и верхнего термов.