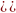- •Геометрические векторы.
- •Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов.
- •Определители n-го порядка. Вычисление и свойства.
- •Матрица. Линейные операции с матрицами. Умножение матриц, обратная матрица.
- •Элемнтарные преобразования матриц. Приведение к ступенчатому виду.
- •Пространство арифметических векторов (линейное пространство).
- •Линейная зависимость. Базис. Линейное пространство в (линейного пространства)
- •Метрические соотношения в Rn
- •Фундаментальная система решений линейного однородного уравнения
- •Изменение матрицы линейного преобразования при изменении базиса
Определители n-го порядка. Вычисление и свойства.
n-порядок определяется в матрице по кол-ву строк и столбцов квадратной матрицы(число строк и столбцов равны). Определитель матрицы – это число, которое постоянно в соответствии целой таблице, т.е. матрицы.
Определитель 1го порядка равен элементу матрицы. Определитель 2го порядка – произведение главной диагонали – произведение побочной диагонали. Определитель 3го порядка: метод треугольн. Определитель не может быть разным у одной и той же матрици каким бы способом его не высчитывали.
Минором
какой-либо квадратной матрицы называется
определитель, полученный из матрицы
путем вычеркивания строки и столбца на
котором он находится
 =
=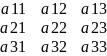
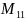 =
=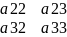 и т.д.
и т.д.
Алгебраическим дополнением какого-либо элемента квадратной матрицы является минор этой матрицы, умноженный на (-1) в стпени №строки+№столбца на пересечении которых он находится.
Свойства определителей:
Определитель не поменяется, если матрицу транспонировать
Перестановка любых 2х строк или столбцов равносильна умножению определителя на -1.
Если в матрице 2 одинаковые строки или столбцы, то опред. = 0. Док-во, т.к. мы меняем местами одинак строки, то опред * на (-1), но строки не меняются, следоват-но определит. = 0.
Если каждый элемент какой-либо строки-столбца определителя умножить на действит число α, то это равносильно произведению всего определителя на число α .
Если в матрице есть 0вая строка или столбец, то опред=0
Если в матрице есть пропорциональные строки, то определитель = 0
Если каждый элемент какого-либо столбца(строки) матрицы представляет собой сумму 2х слагаемых, то определ. Можно представить в виде суммы 2х определителей.
Величина определителя не изменится, если к столбцу, строке прибавить другую стоку, столбец умноженное на действительное число α.
Величина определителя численно равна сумме элементов какой-либо строки или столбца, умноженное на свои алгебр. Дополнения. Разложение определителя по какой-либо строке или столбцу. Определители 4 и более высокого порядка можно вычислить только разложением по строке или столбцу. Перечисленные свойства справедливы для определителей любых порядков больше 1.
Пример
 = 4*
= 4*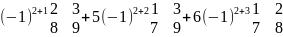 =0
=0
Для облегчения расчетов выбираем столб, где есть хотя бы один 0.
Определитель треугольной матрицы равен произведению элементов на главной диагонали или элементов на побочной диагонали умножен. На (-1) . Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали. Определитель AB равен определителю А умноженный на определитель B.Для нахождения определителя необходимо выделить строку или столбец где больше всего 0,далее как показано в примере сверху.
Матрица. Линейные операции с матрицами. Умножение матриц, обратная матрица.
Матрица
– таблица чисел, состоящая из m
строк и n
столбцов
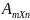
Под линейными операциями над матрицами понимают: сложение матриц, умножение матриц на любое действительное число. Для данных операций справедливо 8 аксиом:
A+B=B+A
A+(B+C)=(A+B)+C
A+θ=A
A+(-A)= θ
1*A=A
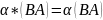
α(A+B)=αA+Αb
(α+β)A=αA+Βa
Умножение матриц. Для перемножения матриц необходимо чтобы кол-во столбцов у 1й матрицы = кол-ву строк у 2й матрицы. Матрица-строка умножается на матрицу столбец. Свойства умножения матриц:
1)A*B≠B*A 2) A*E(1я матрица)=E*A=A
3)A*(BC)=(AB)*C 4) A*(B+C)=AB+AC
5) (A+B)*C=AC+BC (матрицы умножаются строго по порядку)
Обратные
матрицы. Обр. матр. Называется вырожденной,
если ее определитель равен 0, в противном
случае невырожденной. Если С=AB
и определитель С=0, то матрица С-вырожденная
и хотя бы одна из А и B
тоже вырожденная. B
– обратная матрица к А, если справедливо
равенство AB=BA=E
и обозначается
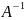 .
Теорема о существовании обратной
матрицы. Если матрица А невырожденная,
то у нее существует обратная матрица,
которая находится по формуле
.
Теорема о существовании обратной
матрицы. Если матрица А невырожденная,
то у нее существует обратная матрица,
которая находится по формуле
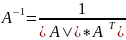 Матрица
Матрица
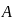 получается из матрицы А заменой каждого
элемента матрицы А его алгебраическим
дополнением. Теорема о единственности
обратной матрицы. Если матрица обратима,
то у нее существует только 1 обратная
матрица. Док-во: предоложим, что у матрицы
А есть 2 обратных матрицы B,C.
Тогда т.к. B
– обратная к А, следовательно AB=BA=E,
но с другой стороны AC=CA=E
Рассмотрим матрицу B=BE
по 5 свойству умножения матриц
B=BE=B(AC)=(BA)C=EC=C,что
противоречит свойству, следовательно
B=C.
Свойства
обратных матриц:
1)
получается из матрицы А заменой каждого
элемента матрицы А его алгебраическим
дополнением. Теорема о единственности
обратной матрицы. Если матрица обратима,
то у нее существует только 1 обратная
матрица. Док-во: предоложим, что у матрицы
А есть 2 обратных матрицы B,C.
Тогда т.к. B
– обратная к А, следовательно AB=BA=E,
но с другой стороны AC=CA=E
Рассмотрим матрицу B=BE
по 5 свойству умножения матриц
B=BE=B(AC)=(BA)C=EC=C,что
противоречит свойству, следовательно
B=C.
Свойства
обратных матриц:
1)
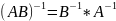 Док-во:
Док-во:
 Докажем, что
Докажем, что
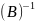 *
*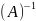 ‑ обратная к (AB)
(AB)(
‑ обратная к (AB)
(AB)(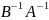 )=A(B
)=A(B )
) =AE
=E(
)(AB)=
(
A)B=
EB=
B=E
Следовательно
– обратная к (AB)
=AE
=E(
)(AB)=
(
A)B=
EB=
B=E
Следовательно
– обратная к (AB)
2)
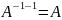 3) |
|=
3) |
|=
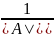 4) определитель транспонированной
матрицы
4) определитель транспонированной
матрицы
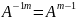 |(
|(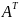 )|=
)|=