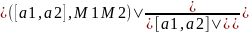- •Геометрические векторы.
- •Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов.
- •Определители n-го порядка. Вычисление и свойства.
- •Матрица. Линейные операции с матрицами. Умножение матриц, обратная матрица.
- •Элемнтарные преобразования матриц. Приведение к ступенчатому виду.
- •Пространство арифметических векторов (линейное пространство).
- •Линейная зависимость. Базис. Линейное пространство в (линейного пространства)
- •Метрические соотношения в Rn
- •Фундаментальная система решений линейного однородного уравнения
- •Изменение матрицы линейного преобразования при изменении базиса
Геометрические векторы.
Рассмотри
на плоскости 2 точки А и Б. По соединяющему
их от резку можно двигаться в обе стороны.
Если А – начало, а Б – конец, получим
направленный отрезок АБ, иначе БА.
Определение – геометрический вектор
– направленный отрезок который можно
перемещать параллельно самому себе.
Если у вектора совпадает начало и конец,
то вектор 0й. Длинной вектора вектора
будем называть величину соответствующей
направлению отрезка или расстояния
между нач. и конечными точками вектора
и обозначается – модуль(AB).
Если длинна вектора равна 1му, то
вектор-единичный. 2 вектора равны, если
они лежат на одной или на параллельных
прямых, направленных в одну сторону и
их длинны равны. 1й вектор имеющий
одинаковое направление с векротом АБ
– орт вектора АБ. Орт = (вектор АБ/длину
вектора). Угол между векторами А и Б –
угол С причем 0<C<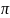 ,
при условии что А и Б имеют общее начало.
,
при условии что А и Б имеют общее начало.
Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов.
Скалярное произведение векторов – число которое находится по формуле |a|*|b|* cos(c), с – угол между векторами. Скалярное произведение (А,Б)=|а|*пр.а Б. = |Б|* пр.б. А.
Свойства скалярного произведения:
(а,б)=(б,а) тк cos(-c) = cos(c);
(а,б+с)= (а,б)+(а,с)
(α*а,б)=(а, α*б)= α(а,б)
(а,а)=|a|*|a| * cos(0) = |a|^2
Скалярное произведение |a|*|a|=0 только тогда, когда вектор а =0
Для того чтобы векторы а и б были ортогональны достаточно, чтобы их векторное произведение равнялось 0.
Скалярное произведение векторов в координатной форме
А{x1,y1,z1} B{x2,y2,z2}
(a,b)= x1x2+y1y2+z1z2
Док-во : рассмотрим 2 вектора в базисе ijk. А=x1i+y1j+z1k, b=x2i+y2j+z2k
(А,B) = (x1i+y1j+z1k, x2i+y2j+z2k)=x1x2(I,j) + x1y1(I,j)+x1z2(I,k)+y1x2(j,i)+y1y2(j,j)+y1z2(j,k)+z1x2(k,i)+z1y2(k,j)+z1z2(k1,k2) т.к i,j,k попарно ортогональны векторное произведение I,j,k = 0, а векторное произведение ijk вектора самого на себя = 1 получаем
(а,б)=x1x2+y1y2+z1z2
Векторное произведение векторов. В векторном произведении [a,b]=с
Такой
что 1) |c|=|a|*|b|*sin(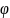 ),
2) вектор с ортогонален плоскости в
которой лежат вектора а и б. 3) вектора
а,б,с расположены таким образом, что из
конца вектора с кратчайший поворот от
вектора а к б виден против часовой
стрелки.(правая тройка векторов)
),
2) вектор с ортогонален плоскости в
которой лежат вектора а и б. 3) вектора
а,б,с расположены таким образом, что из
конца вектора с кратчайший поворот от
вектора а к б виден против часовой
стрелки.(правая тройка векторов)
Свойства векторного произведения:
[a,b]=-[b,a]
[a,b+c]=[a,b]+[a,c]
[a+b,c]=[a,c]+[b,c]
[
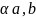 ]=
α[a,b]
]=
α[a,b][a,a]=0
Необходимость
и достаточность условия коллинеарности
векторов для того, чтобы а||б необходимо
и достаточно, чтобы векторное произведение
было равно 0. А||B
если их координаты пропорциональны
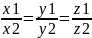 .
.
Геометрический смысл векторного произведения. |[a,b]|= площади параллелограмма, построенного на векторах а и б. Векторное произведение в координатной форме.
А={x1,y1,z1} b={x2,y2,z2}
[a,b]=
 = определитель 3-го порядка вычисл. По
формуле:
= определитель 3-го порядка вычисл. По
формуле:
I*|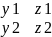 |
- J*|
|
- J*|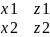 |
+ K*|
|
+ K*|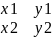 |
Получаем определители 2-го порядка,
которые вычисляются по формуле
(y1*z2-z1*y2)
получаем [a,b]={x3,y3,z3}
|
Получаем определители 2-го порядка,
которые вычисляются по формуле
(y1*z2-z1*y2)
получаем [a,b]={x3,y3,z3}
Смешенные произведения векторов
Смешенным произведением векторов называется число равное векторному произведению 2х векторов [a,b] скалярно умноженные на вектор c
([a,b],c)
Условие компланарности 3х векторов(лежат в одной плоскости) их смешенное произведение равно 0.Геометрический смысл смеш. Произв. – объем параллелепипеда построенного на векторах a,b,c численно равен их смешенному произведению. Смешенное произведение в координатной форме.
([a,b],c)=
|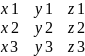 |
= x1*|
|
= x1*|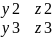 |
- y1*|
|
- y1*|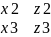 |+
z1*
|
|+
z1*
| |
|
Плоскость и прямая в пространстве. Основные задачи о прямых и плоскостях.
Уравнение
плоскости α
проходящую через точку Мо перпендикулярн.
Вектору
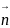 A(x-x0)+B(y-y0)+c(z-z0)=0
Мо{x0,y0,z0}
n{A,B,C}
M{x,y,z}
A(x-x0)+B(y-y0)+c(z-z0)=0
Мо{x0,y0,z0}
n{A,B,C}
M{x,y,z}
Полученное уравнение является (ММо,n) n-нормальный вектор перпендик к плоскости α. Преобразуем уравнение A(x-x0)+B(y-y0)+c(z-z0)=Ax-Axo+By-Byo+Cz-Czo=0 D=-Axo-Byo-Czo – число Ax+By+Cz+D=0(общее уравнение плоскости)
Угол
между плоскостями
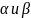 – угол, полученный при пересечении этих
плоскостей, причем 1 из углов будет равен
углу при пересечении нормальных векторов
n1
и n2.
– угол, полученный при пересечении этих
плоскостей, причем 1 из углов будет равен
углу при пересечении нормальных векторов
n1
и n2.
α: A1x+B1y+C1z+D1=0 n1={A1,B1,C1}
β: A2x+B2y+C2z+D2=0 n2={A2,B2,C2}
Из
скалярного произведения векторов
φ=arcos(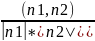 )
=
)
=
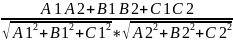
Уравнение плоскости, проходящую через 3 данные точки.
М1(x1,y1,z1); M2(x2,y2,z2); M3(x3,y3,z3)
Тогда произведение точка пространства с координатами x,y,z будет принадлежать плоскости когда M1M, M1M3, M1M2 будут компланарны, а значит их смешенное произведение будет равно 0. (M1M,[M1M3,M1M2])=0
M1M{x-x1;y-y1;z-z1}
M1M2{x2-x1;y2-y1;z2-z1}
M1M3{x3-x1;y3-y1;z3-z1}
α:
|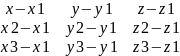 |
Решаем уравнение, приравниваем к 0 и
получаем уравнение плоскости.
|
Решаем уравнение, приравниваем к 0 и
получаем уравнение плоскости.
Уравнение плоскости в отрезках.
Рассмотрим общее уравнение плоскости α, которое не проходит через начало координат, при этом D≠0
α:
Ax+By+Cz=
‑D|÷
(‑D)
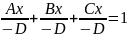 Вынесем в знаменатель A,B,C
Вынесем в знаменатель A,B,C
a=(-D/A),
b=(-D/B),
c=(-D/c)
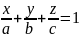 – уравнение плоскости α в отрезках
отсекаемых этой плоскостью от координатных
осей. Плоскость заданную таким образом
легко строить, т.к. она проходит через
точки (a;0;0),(0;b;0),
(0;0;c)
– уравнение плоскости α в отрезках
отсекаемых этой плоскостью от координатных
осей. Плоскость заданную таким образом
легко строить, т.к. она проходит через
точки (a;0;0),(0;b;0),
(0;0;c)
Уравнение плоскости проходящее через начало координат. D=0
Ax+Bx+Cx=0 Ax+By+D=0 –уравнение плоскости || OZ
N{0,0,1}, Ax+Cz+D=0 - || OY By+Cz+D=0 ||OX Ax+D=0 ||YOZ
Пример: найти расстояние от Мо {x,y,z} до плоскости α проходящей через точки М1{x1,y1,z1},М2{x2,y2,z2},М3{x3,y3,z3}. Для этого необходимо найти нормальный вектор n плоскости α, расстояние от Мо до α будет равен проекции ММо на n, т.е |MMo|*cos(β) β- угол между n и MMo. N=[M1M2,M1M3] (n,MMo)=|n|*|MMo|*cos(β).
Линия
в пространстве – как частный случай –
линия пересечения 2х плоскостей. Для
решения щадач неудобно использовать
общее уравнение прямой
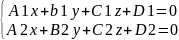
Каноническое уравнение прямой:
n1={A1,B1,C1} ǂǂ n2={A2,B2,C2}. Рассмотрим прямую D которая проходит через точку Мо{Xo,Yo,Zo}, которая принадлежит прямой D. A{l,m,n}-направляющий вектор прямой D. Тогда произвольная точка пространства M{x,y,z} будет принадлежать прямой D только тогда когда MoM||a.
MoM{x-xo;y-yo;z-zo}, если их координаты пропорциональны и
D=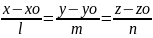
Параметрическое уравнение прямой:
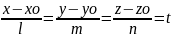
x=lt+xo y=yo+mt z=zo+nt ‑‑‑‑‑‑ параметрическое ур-е прямой.
Пример: составить каноническое уравнение прямой проходящ через 2 точки
М1(x1,y1,z1) M2(x2,y2,z2) ,берем любую из точек, лежащую на прямой к примеру М1, а за направляющий вектор возьмем вектор М1М2. Получим
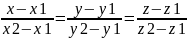 =t
Параметрическое уравнение прямой:
x=tx2-tx1+x1
=t
Параметрическое уравнение прямой:
x=tx2-tx1+x1
Y=ty2-ty1+y1, z=tz2-tz1+z1 Общее уравнение прямой: D-линия пересечения бесконечного множества плоскостей в том числе и следующих 2х.
(x-x1)/(x2-x1)=(y-y1)/(y2-y1) (x-x1)/(x2-x1)=(z-z1)/(z2-z1)
Подставив числа получим неполное уравнение плоскости. Одна или даже 2 координаты направляющего вектора прямой могут равняться 0, т.е. в каноническом уравнении в знаменателе может стоять 0, и это будет не деление на 0, а отношением к 0.
Составление канонического уравнения прямой как пересечение 2х плоскостей.
D= Любая прямая в пространстве пересекает хотя бы одну координатную плоскость, поэтому за точку прямой можно взять точку пересечения данной плоскости и и координатной плоскости приравняв соответствующую координату к 0. Если при этом получится система, которая не имеет решений, значит данная прямая не пересекает данную плоскость и следует рассмотреть точку пересечения этой прямой с какой-нибудь другой плоскостью. Получим несколько точек лежащих на данной прямой. Направляющий вектор нашей прямой || последней следовательно он || заданным плоскостям и перпендикулярен нормальным векторам наших плоскостей, а это значит что направляющий вектор А=[n1,n2]. Находим произведение и подставляем в уравнение D=
Найти Точку пересечения прямой D и плоскости α. Прямая пересекает плоскость в 1м месте, если направляющий вектор А, прямой D не перпендикулярен нормальному вектору n плоскости. (n,a)≠0, тогда есть точка пересечения. Для нахождения необходимо приравнять параметрическое уравнение прямой к уравнению плоскости.
Найти
координаты проекции в точке Р(1.0.1) на
плоскость
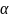 :
4x+6y+4z-25=0
:
4x+6y+4z-25=0
Проекция P есть точка пересечения прямой D проходящей через точку Р и плоскость α. Нормаль к - направляющий вектор прямой D. Составляем параметрическое уравнение прямой и решаем систему.
Найти
точку симметричную точке Р(1.-1.3)
относительно прямой d:
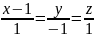 Строим плоскость α, которой будет
принадлежать точка Р, причем α
перпендикулярна d,
cледовательно
нормальный вектор к плоскости α равен
направляющему вектору прямой D.
N=a{1;-1;1}
ур-е плоскости
Строим плоскость α, которой будет
принадлежать точка Р, причем α
перпендикулярна d,
cледовательно
нормальный вектор к плоскости α равен
направляющему вектору прямой D.
N=a{1;-1;1}
ур-е плоскости
1(x-0)-1(y+1)+1(z-3)=0 α: x-y+z-4=0 Теперь найдем точку пересечения прямой и плоскости приравняв уравнения прямой и плоскости. Q=(2;-1;1) Вектор PQ равен вектору P1Q Следовательно Q – середина PP1
X(q)=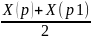 Находим Xp1
также для координат y
и z
и получаем точку симметричную данной
относительно прямой.
Находим Xp1
также для координат y
и z
и получаем точку симметричную данной
относительно прямой.
Взаимное расположение прямых в пространстве.
Прямые а || b если их направляющие векторы ||.
Найдем
расстояние от точки Мо(xo,yo,zo) до прямой
D
в пространстве. D=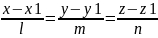 M1(x1,y1,z1)
a1||a
a1принадлежит
d
достроим до параллелограмма
М1Мо={xo-x1,yo-y1,z0-z1}
s=|[M1Mo,a]|
s=|a1|*h
M1(x1,y1,z1)
a1||a
a1принадлежит
d
достроим до параллелограмма
М1Мо={xo-x1,yo-y1,z0-z1}
s=|[M1Mo,a]|
s=|a1|*h
H=
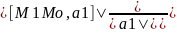
Расстояние между скрещивающимися прямыми.
А:
=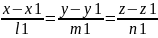 B:=
B:=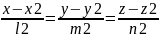
Их направляющие вектора равны a1 и a2
Возьмем 2 точки М1 на а и М2 на b M1M2={x2-x1;y2-y1;z2-z1}
H=